2021届高考数学一轮复习第八章立体几何与空间向量第4节直线平面平行的判定与性质课件新人教A版 38页

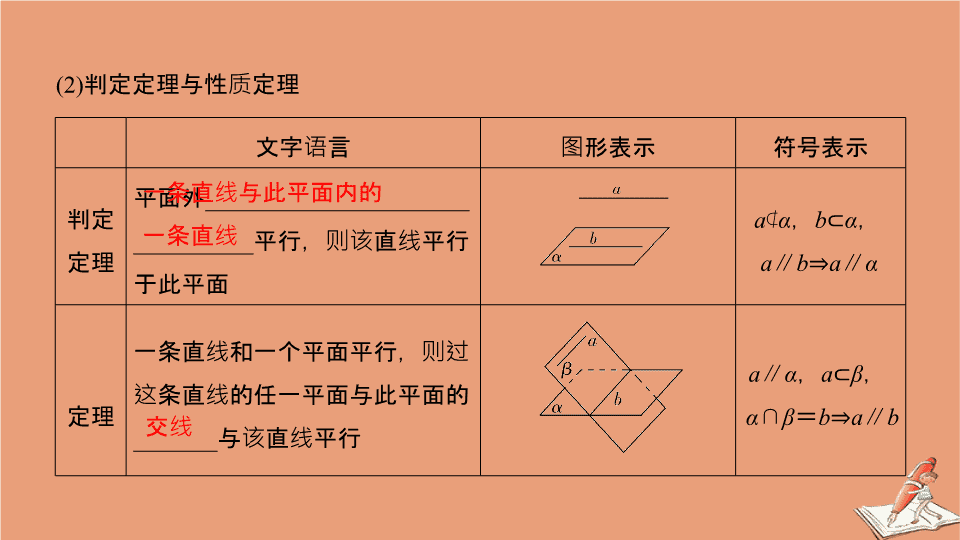
第 4 节　直线、平面平行的判定与性质 考试要求　 1. 以立体几何的定义、公理和定理为出发点，认识和理解空间中线面平行的有关性质与判定定理； 2. 能运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题 . 知 识 梳 理 1. 直线与平面平行 (1) 直线与平面平行的定义 直线 l 与平面 α 没有公共点，则称直线 l 与平面 α 平行 . (2) 判定定理与性质定理 文字语言 图形表示 符号表示 判定 定理 平面外 ______________________ __________ 平行，则该直线平行于此平面 a ⊄ α ， b ⊂ α ， a ∥ b ⇒ a ∥ α   定理 一条直线和一个平面平行，则过这条直线的任一平面与此平面的 _______ 与该直线平行 a ∥ α ， a ⊂ β ， α ∩ β ＝ b ⇒ a ∥ b 一条直线与此平面内的 一条直线 交线 2. 平面与平面平行 (1) 平面与平面平行的定义 没有公共点的两个平面叫做平行平面 . (2) 判定定理与性质定理   文字语言 图形表示 符号表示 判定 定理 一个平面内的两 条 _________ 与 另一个平面平行，则这两个平面平行 a ⊂ α ， b ⊂ α ， a ∩ b ＝ P ， a ∥ β ， b ∥ β ⇒ α ∥ β 相交直线 性质 定理 两个平面平行，则其中一个平面内的 直线 _______ 于 另一个平面 α ∥ β ， a ⊂ α ⇒ a ∥ β 如果两个平行平面同时和第三个平面相交，那么它们 的 _______ 平行 α ∥ β ， α ∩ γ ＝ a ， β ∩ γ ＝ b ⇒ a ∥ b 平行 交线 [ 常用结论与微点提醒 ] 1. 平行关系中的三个重要结论 (1) 垂直于同一条直线的两个平面平行，即若 a ⊥ α ， a ⊥ β ，则 α ∥ β . (2) 平行于同一平面的两个平面平行，即若 α ∥ β ， β ∥ γ ，则 α ∥ γ . (3) 垂直于同一个平面的两条直线平行，即若 a ⊥ α ， b ⊥ α ，则 a ∥ b . 2. 三种平行关系的转化 线线平行、线面平行、面面平行的相互转化是解决与平行有关的证明题的指导思想，解题中既要注意一般的转化规律，又要看清题目的具体条件，选择正确的转化方向 . 诊 断 自 测 1. 判断下列结论正误 ( 在括号内打 “√” 或 “×” ) (1) 若一条直线和平面内一条直线平行，那么这条直线和这个平面平行 .( 　　 ) (2) 若直线 a ∥ 平面 α ， P ∈ α ，则过点 P 且平行于直线 a 的直线有无数条 .( 　　 ) (3) 如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行 .( 　　 ) (4) 如果两个平面平行，那么分别在这两个平面内的两条直线平行或异面 .( 　　 ) 解析　 (1) 若一条直线和平面内的一条直线平行，那么这条直线和这个平面平行或在平面内，故 (1) 错误 . (2) 若 a ∥ α ， P ∈ α ，则过点 P 且平行于 a 的直线只有一条，故 (2) 错误 . (3) 如果一个平面内的两条直线平行于另一个平面，则这两个平面平行或相交，故 (3) 错误 . 答案　 (1) × 　 (2) × 　 (3) × 　 (4) √ 2. ( 老教材必修 2P61A 组 T1(2) 改编 ) 下列说法中，与 “ 直线 a ∥ 平面 α ” 等价的是 ( 　　 ) A. 直线 a 上有无数个点不在平面 α 内 B. 直线 a 与平面 α 内的所有直线平行 C. 直线 a 与平面 α 内无数条直线不相交 D. 直线 a 与平面 α 内的任意一条直线都不相交 解析　 因为 a ∥ 平面 α ，所以直线 a 与平面 α 无交点，因此 a 和平面 α 内的任意一条直线都不相交，故选 D. 答案　 D 3. ( 新教材必修第二册 P142T2 改编 ) 平面 α ∥ 平面 β 的一个充分条件是 ( 　　 ) A. 存在一条直线 a ， a ∥ α ， a ∥ β B. 存在一条直线 a ， a ⊂ α ， a ∥ β C. 存在两条平行直线 a ， b ， a ⊂ α ， b ⊂ β ， a ∥ β ， b ∥ α D. 存在两条异面直线 a ， b ， a ⊂ α ， b ⊂ β ， a ∥ β ， b ∥ α 解析　 若 α ∩ β ＝ l ， a ∥ l ， a ⊄ α ， a ⊄ β ， a ∥ α ， a ∥ β ，故排除 A ； 若 α ∩ β ＝ l ， a ⊂ α ， a ∥ l ，则 a ∥ β ，故排除 B ； 若 α ∩ β ＝ l ， a ⊂ α ， a ∥ l ， b ⊂ β ， b ∥ l ，则 a ∥ β ， b ∥ α ，故排除 C ； 故选 D. 答案　 D 4. (2020· 洛阳尖子生联考 ) 设 l ， m 是两条不同的直线， α ， β 是两个不同的平面，且 l ⊂ α ， m ⊂ β ，下列结论正确的是 ( 　　 ) A. 若 α ⊥ β ，则 l ⊥ β B. 若 l ⊥ m ，则 α ⊥ β C. 若 α ∥ β ，则 l ∥ β D. 若 l ∥ m ，则 α ∥ β 解析　 对于 A ， α ⊥ β ， l ⊂ α ，只有加上 l 垂直于 α 与 β 的交线，才有 l ⊥ β ，所以 A 错误；对于 B ，若 l ⊥ m ， l ⊂ α ， m ⊂ β ，则 α 与 β 可能平行，也可能相交但不垂直，所以 B 错误；对于 C ，若 α ∥ β ， l ⊂ α ，由面面平行的性质可知， l ∥ β ，所以 C 正确；对于 D ，若 l ∥ m ， l ⊂ α ， m ⊂ β ，则 α 与 β 可能平行，也可能相交，所以 D 错误 . 答案　 C 5. (2019· 成都月考 ) 若平面 α ∥ 平面 β ，直线 a ∥ 平面 α ，点 B ∈ β ，则在平面 β 内且过 B 点的所有直线中 ( 　　 ) A. 不一定存在与 a 平行的直线 B. 只有两条与 a 平行的直线 C. 存在无数条与 a 平行的直线 D. 存在唯一与 a 平行的直线 解析　 当直线 a 在平面 β 内且过 B 点时，不存在与 a 平行的直线，故选 A. 答案　 A 6. (2019· 衡水中学开学考试 ) 如图是长方体被一平面所截得的几何体，四边形 EFGH 为截面，则四边形 EFGH 的形状为 ________. 解析　 ∵ 平面 ABFE ∥ 平面 DCGH ， 又平面 EFGH ∩ 平面 ABFE ＝ EF ， 平面 EFGH ∩ 平面 DCGH ＝ HG ， ∴ EF ∥ HG . 同理 EH ∥ FG ， ∴ 四边形 EFGH 是平行四边形 . 答案　 平行四边形 ① 若 a ∥ c ， b ∥ c ，则 a ∥ b ； ② 若 a ∥ b ， b ∥ α ，则 a ∥ α ； ③ 若 a ∥ α ， b ∥ α ，则 a ∥ b . 其中真命题的个数是 ( 　　 ) A.0 B.1 C.2 D.3 考点一　与线、面平行相关命题的判定 【例 1 】 (1) (2019· 长沙模拟 ) 设 a ， b ， c 表示不同直线， α ， β 表示不同平面，给出下列命题： (2) (2020· 江西红色七校联考 ) 设 m ， n 是空间中两条不同的直线， α ， β 是两个不同的平面，则下列说法正确的是 ( 　　 ) A. 若 m ∥ n ， n ⊂ α ，则 m ∥ α B. 若 m ⊂ α ， n ⊂ β ， α ∥ β ，则 m ∥ n C. 若 α ∥ β ， m ⊥ α ，则 m ⊥ β D. 若 m ⊂ α ， n ⊂ β ， m ∥ β ， n ∥ α ，则 α ∥ β 解析　 (1) 对于 ① ，根据线线平行的传递性可知 ① 是真命题；对于 ② ，由 a ∥ b ， b ∥ α ，可以推出 a ∥ α 或 a ⊂ α ，故 ② 是假命题；对于 ③ ，根据 a ∥ α ， b ∥ α ，可以推出 a 与 b 平行、相交或异面，故 ③ 是假命题 . 故选 B. (2) 若 m ∥ n ， n ⊂ α ，则 m ∥ α 或 m ⊂ α ，所以选项 A 不正确；若 m ⊂ α ， n ⊂ β ， α ∥ β ，则 m ∥ n 或 m 与 n 异面，所以选项 B 不正确；若 m ⊂ α ， n ⊂ β ， m ∥ β ， n ∥ α ，则 α ∥ β 或 α 与 β 相交，所以选项 D 不正确 . 故选 C. 答案　 (1)B 　 (2)C 规律方法　 1. 判断与平行关系相关命题的真假，必须熟悉线、面平行关系的各个定义、定理，无论是单项选择还是含选择项的填空题，都可以从中先选出最熟悉最容易判断的选项先确定或排除，再逐步判断其余选项 . 2.(1) 结合题意构造或绘制图形，结合图形作出判断 . (2) 特别注意定理所要求的条件是否完备，图形是否有特殊情况，通过举反例否定结论或用反证法推断命题是否正确 . 【训练 1 】 (1) (2019· 全国 Ⅱ 卷 ) 设 α ， β 为两个平面，则 α ∥ β 的充要条件是 ( 　　 ) A. α 内有无数条直线与 β 平行 B. α 内有两条相交直线与 β 平行 C. α ， β 平行于同一条直线 D. α ， β 垂直于同一平面 (2) 在正方体 ABCD － A 1 B 1 C 1 D 1 中，下列结论正确的是 ________( 填序号 ). ① AD 1 ∥ BC 1 ； ② 平面 AB 1 D 1 ∥ 平面 BDC 1 ； ③ AD 1 ∥ DC 1 ； ④ AD 1 ∥ 平面 BDC 1 . 解析　 (1) 若 α ∥ β ，则 α 内有无数条直线与 β 平行，当无数条直线互相平行时， α 与 β 可能相交；若 α ， β 平行于同一条直线，则 α 与 β 可以平行也可以相交；若 α ， β 垂直于同一个平面，则 α 与 β 可以平行也可以相交，故 A ， C ， D 中条件均不是 α ∥ β 的充要条件 . 根据两平面平行的判定定理知，若一个平面内有两条相交直线与另一个平面平行，则两平面平行，反之也成立 . 因此 B 中条件是 α ∥ β 的充要条件 . (2) 如图，因为 AB 綉 C 1 D 1 ， 所以四边形 AD 1 C 1 B 为平行四边形 . 故 AD 1 ∥ BC 1 ，从而 ① 正确； 易证 BD ∥ B 1 D 1 ， AB 1 ∥ DC 1 ， 又 AB 1 ∩ B 1 D 1 ＝ B 1 ， BD ∩ DC 1 ＝ D ， 故平面 AB 1 D 1 ∥ 平面 BDC 1 ，从而 ② 正确； 由图易知 AD 1 与 DC 1 异面，故 ③ 错误； 因为 AD 1 ∥ BC 1 ， AD 1 ⊄ 平面 BDC 1 ， BC 1 ⊂ 平面 BDC 1 ， 所以 AD 1 ∥ 平面 BDC 1 ，故 ④ 正确 . 答案　 (1)B 　 (2) ①②④ (1) 求证： AB ∥ 平面 ECD ； (2) 求三棱锥 E － ACD 的体积 . (1) 证明　 取 CD 的中点 M ，连接 EM ， BM . 因为 CE ＝ ED ，所以 EM ⊥ CD . 因为平面 ECD ⊥ 平面 BCD ，且平面 ECD ∩ 平面 BCD ＝ CD ， EM ⊂ 平面 ECD ， 所以 EM ⊥ 平面 BCD . 因为 AB ⊥ 平面 BCD ，所以 AB ∥ EM . 又 EM ⊂ 平面 ECD ， AB ⊄ 平面 ECD ， 所以 AB ∥ 平面 ECD . (2) 解　 因为原四边形 BCED 为正方形， M 为 CD 的中点，所以 BM ⊥ CD . 又因为平面 ECD ⊥ 平面 BCD ，且平面 ECD ∩ 平面 BCD ＝ CD ， BM ⊂ 平面 BCD ， 所以 BM ⊥ 平面 ECD . 角度 2 　直线与平面平行性质定理的应用 【例 2 － 2 】 如图，在直四棱柱 ABCD － A 1 B 1 C 1 D 1 中， E 为线段 AD 上的任意一点 ( 不包括 A ， D 两点 ) ，平面 CEC 1 与平面 BB 1 D 交于 FG . 证明： FG ∥ 平面 AA 1 B 1 B . 证明　 在四棱柱 ABCD － A 1 B 1 C 1 D 1 中 ， BB 1 ∥ CC 1 ， BB 1 ⊂ 平面 BB 1 D ， CC 1 ⊄平面 BB 1 D ， 所以 CC 1 ∥ 平面 BB 1 D . 又 CC 1 ⊂ 平面 CEC 1 ， 平面 CEC 1 与平面 BB 1 D 交于 FG ， 所以 CC 1 ∥ FG . 因 为 BB 1 ∥ CC 1 ， 所以 BB 1 ∥ FG . 而 BB 1 ⊂ 平面 AA 1 B 1 B ， FG ⊄ 平面 AA 1 B 1 B ， 所以 FG ∥ 平面 AA 1 B 1 B . 规律方法　 1. 利用判定定理判定线面平行，关键是找平面内与已知直线平行的直线 . 常利用三角形的中位线、平行四边形的对边或过已知直线作一平面找其交线 . 2. 在解决线面、面面平行的判定时，一般遵循从 “ 低维 ” 到 “ 高维 ” 的转化，即从 “ 线线平行 ” 到 “ 线面平行 ” ，再到 “ 面面平行 ” ；而在应用性质定理时，其顺序恰好相反 . 【训练 2 】 (2019· 太原一模 ) 如图，在四棱锥 E － ABCD 中，底面 ABCD 是平行四边形， M ， N 分别是 BC ， DE 的中点， △ ABE 是等边三角形，平面 ABE ⊥ 平面 BCE ， BE ⊥ CE ， BE ＝ CE ＝ 2. (1) 求证： CN ∥ 平面 AEM ； (2) 求三棱锥 N － AEM 的体积 . (1) 证明　 如图，设 AE 的中点为 F ，连接 MF ， NF . ∵ 四边形 ABCD 是平行四边形， ∴ AD ∥ BC ， AD ＝ BC . ∴ 四边形 MCNF 是平行四边形， ∴ CN ∥ MF . 又 MF ⊂ 平面 AEM ， CN ⊄ 平面 AEM ， ∴ CN ∥ 平面 AEM . (2) 解　 如图，过点 A 作 AO ⊥ BE ， O 为垂足，连接 AC . ∵ 平面 ABE ⊥ 平面 BCE ，平面 ABE ∩ 平面 BCE ＝ BE ， ∴ AO ⊥ 平面 BCE . 考点三　面面平行的判定与性质　 典例迁移 【例 3 】 ( 经典母题 ) 如图所示，在三棱柱 ABC － A 1 B 1 C 1 中， E ， F ， G ， H 分别是 AB ， AC ， A 1 B 1 ， A 1 C 1 的中点，求证： (1) B ， C ， H ， G 四点共面； (2) 平面 EFA 1 ∥ 平面 BCHG . 证明　 (1) ∵ G ， H 分别是 A 1 B 1 ， A 1 C 1 的中点， ∴ GH 是 △ A 1 B 1 C 1 的中位线，则 GH ∥ B 1 C 1 . 又 ∵ B 1 C 1 ∥ BC ， ∴ GH ∥ BC ， ∴ B ， C ， H ， G 四点共面 . (2) ∵ E ， F 分别为 AB ， AC 的中点， ∴ EF ∥ BC ， ∵ EF ⊄ 平面 BCHG ， BC ⊂ 平面 BCHG ， ∴ EF ∥ 平面 BCHG . 又 G ， E 分别为 A 1 B 1 ， AB 的中点， A 1 B 1 綉 AB ， ∴ A 1 G 綉 EB ， ∴ 四边形 A 1 EBG 是平行四边形， ∴ A 1 E ∥ GB . ∵ A 1 E ⊄ 平面 BCHG ， GB ⊂ 平面 BCHG ， ∴ A 1 E ∥ 平面 BCHG . 又 ∵ A 1 E ∩ EF ＝ E ， ∴ 平面 EFA 1 ∥ 平面 BCHG . 【迁移 1 】 在本例中，若将条件 “ E ， F ， G ， H 分别是 AB ， AC ， A 1 B 1 ， A 1 C 1 的中点 ” 变为 “ D 1 ， D 分别为 B 1 C 1 ， BC 的中点 ” ，求证：平面 A 1 BD 1 ∥ 平面 AC 1 D . 证明　 如图所示，连接 A 1 C 交 AC 1 于点 M ， ∵ 四边形 A 1 ACC 1 是平行四边形， ∴ M 是 A 1 C 的中点，连接 MD ， ∵ D 为 BC 的中点， ∴ A 1 B ∥ DM . ∵ A 1 B ⊂ 平面 A 1 BD 1 ， DM ⊄ 平面 A 1 BD 1 ， ∴ DM ∥ 平面 A 1 BD 1 ， 又由三棱柱的性质及 D ， D 1 分别为 BC ， B 1 C 1 的中点知， D 1 C 1 綉 BD ， ∴ 四边形 BDC 1 D 1 为平行四边形， ∴ DC 1 ∥ BD 1 . 又 DC 1 ⊄ 平面 A 1 BD 1 ， BD 1 ⊂ 平面 A 1 BD 1 ， ∴ DC 1 ∥ 平面 A 1 BD 1 ， 又 DC 1 ∩ DM ＝ D ， DC 1 ， DM ⊂ 平面 AC 1 D ， 因此平面 A 1 BD 1 ∥ 平面 AC 1 D . 解　 连接 A 1 B 交 AB 1 于 O ， 连接 OD 1 . 由平面 BC 1 D ∥ 平面 AB 1 D 1 ， 且平面 A 1 BC 1 ∩ 平面 BC 1 D ＝ BC 1 ， 平面 A 1 BC 1 ∩ 平面 AB 1 D 1 ＝ D 1 O ， 规律方法　 1. 判定面面平行的主要方法 (1) 利用面面平行的判定定理 . (2) 线面垂直的性质 ( 垂直于同一直线的两平面平行 ). 2. 面面平行条件的应用 (1) 两平面平行，分析构造与之相交的第三个平面，交线平行 . (2) 两平面平行，其中一个平面内的任意一条直线与另一个平面平行 . 提醒　 利用面面平行的判定定理证明两平面平行，需要说明是在一个平面内的两条直线是相交直线 . 【训练 3 】 已知四棱柱 ABCD － A 1 B 1 C 1 D 1 中， AD ∥ BC ， AD ＝ 2 BC ， E ， F 分别为 CC 1 ， DD 1 的中点 . 求证：平面 BEF ∥ 平面 AD 1 C 1 . 证明　 取 AD 的中点 G ，连接 BG ， FG . 因为 E ， F 分别为 CC 1 ， DD 1 的中点，所以 C 1 D 1 綉 CD 綉 EF ， 因为 C 1 D 1 ⊂ 平面 AD 1 C 1 ， EF ⊄ 平面 AD 1 C 1 ，所以 EF ∥ 平面 AD 1 C 1 . 因为 AD ∥ BC ， AD ＝ 2 BC ， 所以 GD 綉 BC ，即四边形 BCDG 是平行四边形， 所以 BG 綉 CD ，所以 BG 綉 EF ，即四边形 EFGB 是平行四边形，所以 BE ∥ FG . 因为 F ， G 分别是 DD 1 ， AD 的中点，所以 FG ∥ AD 1 ，所以 BE ∥ AD 1 . 因为 AD 1 ⊂ 平面 AD 1 C 1 ， BE ⊄ 平面 AD 1 C 1 ，所以 BE ∥ 平面 AD 1 C 1 . 又 BE ⊂ 平面 BEF ， FE ⊂ 平面 BEF ， BE ∩ EF ＝ E ， 所以平面 BEF ∥ 平面 AD 1 C 1 .