- 437.50 KB
- 2021-06-16 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
www.ks5u.com
探秘基本初等函数的命题热点动向
微点聚焦突破
以二次函数、幂函数、指数与对数函数为载体考查函数图象与性质,灵活利用图象、性质解决与方程(不等式)的交汇融合问题,相关参数求解与讨论一直是命题的热点,常以客观题的形式呈现,考查学生数学运算、直观想象、逻辑推理数学核心素养.
类型一 基本初等函数图象的辨析
角度1 特殊值与性质检验法
【例1-1】 (1)函数f(x)=x2-的大致图象是( )
(2)(2019·福州质检)函数f(x)=x2+ln(e-x)ln(e+x)的大致图象为( )
解析 (1)由f(0)=-1,知图象过点(0,-1),排除D项.
又f(-2)=4-4=0,f(-4)=16-16=0,
∴f(x)的图象过点(-2,0),(-4,0),排除A,C,只有B适合.
(2)易知f(-x)=(-x)2+ln(e+x)ln(e-x)=x2+ln(e-x)ln(e+x)=f(x),
∴y=f(x)的图象关于y轴对称,排除C项.
又当x→e时,f(x)→-∞,排除选项B,D.
答案 (1)B (2)A
思维升华 1.求解该类问题抓住两点:(1)根据函数的奇偶性、周期性、单调性排除不符合的选项.(2)利用特殊值(点)或极限的思想,排除不可能选项.
2.注意两点:(1)特殊点或特殊值要具备特殊性和代表性,只能否定错误的结论.(2)紧扣图象特征,揭示函数的性质.
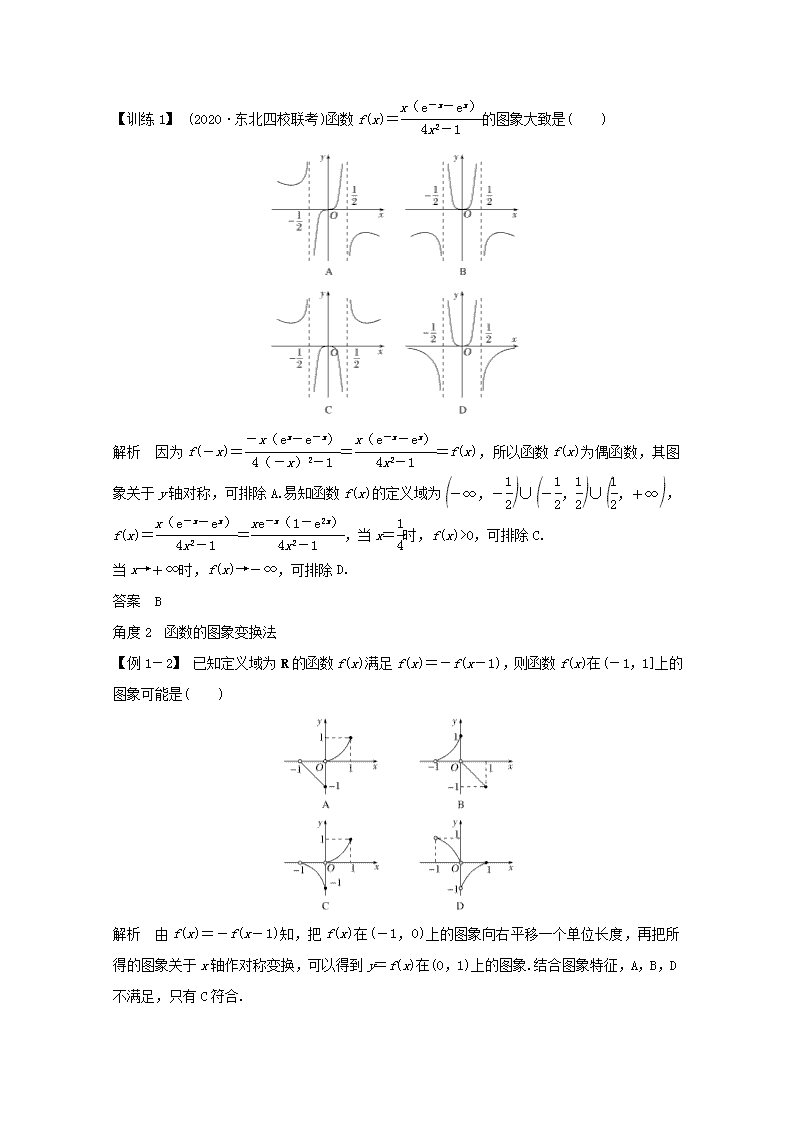
【训练1】 (2020·东北四校联考)函数f(x)=的图象大致是( )
解析 因为f(-x)===f(x),所以函数f(x)为偶函数,其图象关于y轴对称,可排除A.易知函数f(x)的定义域为∪∪,f(x)==,当x=时,f(x)>0,可排除C.
当x→+∞时,f(x)→-∞,可排除D.
答案 B
角度2 函数的图象变换法
【例1-2】 已知定义域为R的函数f(x)满足f(x)=-f(x-1),则函数f(x)在(-1,1]上的图象可能是( )
解析 由f(x)=-f(x-1)知,把f(x)在(-1,0)上的图象向右平移一个单位长度,再把所得的图象关于x轴作对称变换,可以得到y=f(x)在(0,1)上的图象.结合图象特征,A,B,D不满足,只有C符合.
答案 C
思维升华 1.通过图象变换识别函数图象要掌握两点:一是熟悉基本初等函数的图象(如指数函数、对数函数等函数的图象);二是了解一些常见的变换形式,如平移变换、伸缩变换、翻折变换.
2.函数图象进行左右平移变换,一定是仅仅相对于“自变量x”而言的,一定把x的系数变为1.
【训练2】 (2020·武汉部分重点中学联考)已知函数y=sin ax+b(a>0)的图象,如图所示,则函数y=loga(x+b)的图象可能是( )
解析 由y=sin ax+b的图象知,周期T>2π,02π,∴00,则下列关系式不可能成立的是( )
A.<< B.<<
C.<< D.==
解析 令log2x=log3y=log5z=k>0,
则x=2k>1,y=3k>1,z=5k>1,
故=2k-1,=3k-1,=5k-1,
若01时,则f(x)=xk-1在(0,+∞)上单调递增,
∴<<,选项A成立.
综上,选项A,B,D都有可能成立,只有C不成立.
答案 C
思维升华 1.本题考查对数定义,幂函数、指数函数的单调性及应用,着重考查逻辑推理、数学运算等数学核心素养.
2.运用基本初等函数性质求解问题,要注意不同参数取值对性质的影响,必要时要进行分类讨论.
【训练3】 若函数f(x)=x2,设a=log54,b=log,c=2,则f(a),f(b),f(c)的大小关系是( )
A.f(a)>f(b)>f(c) B.f(b)>f(c)>f(a)
C.f(c)>f(b)>f(a) D.f(c)>f(a)>f(b)
解析 由b=log=log53,且y=log5x是增函数,
∴1>a>b>0,
又c=2>1,且f(x)=x2在(0,+∞)上是增函数,
∴f(c)>f(a)>f(b).
答案 D
角度2 利用性质求函数值或范围
【例2-2】 (1)(2020·安徽名校联考)已知函数y=g(x)满足g(x+2)=-g(x),若y=f(x
)在(-2,0)∪(0,2)上为偶函数,且其解析式为f(x)=则g(-2 021)的值为( )
A.-1 B.0 C. D.-
(2)(2020·石家庄调研)已知函数f(x)=2x+log3,若不等式f>3成立,则实数m的取值范围是( )
A.(1,+∞) B.(-∞,1)
C. D.
解析 (1)由g(x+2)=-g(x),得g(x+4)=g(x),
∴4是函数g(x)的周期.
则g(-2 021)=g(-505×4-1)=g(-1).
又f(x)在(-2,0)∪(0,2)上是偶函数,
∴g(-1)=f(-1)=f(1)=log21=0.
(2)由>0,得f(x)的定义域为(-2,2).
∵y=log3=log3在(-2,2)上单调递增,
∴f(x)在(-2,2)上是增函数.
又f(1)=3,f>3⇔f>f(1).
∴解得f(x)的x的取值范围是( )
A.(-∞,-1)∪(2,+∞)
B.(-∞,-)∪(,+∞)
C.(-∞,-)∪(2,+∞)
D.(-∞,-1)∪(,+∞)
解析 当x>0时,f(x)=2x-2-x是增函数;
当x≤0时,f(x)=0.
由f(x2-2)>f(x),∴或
解得x>2或x<-.
故不等式的解集为(-∞,-)∪(2,+∞).
答案 C
类型三 运用基本初等函数图象性质解零点问题
【例3】 (2019·湖北重点中学联考)已知函数f(x)=,若关于x的方程[f(x)]2+mf(x)+m-1=0恰有3个不同的实数解,则实数m的取值范围是( )
A.(-∞,2)∪(2,+∞) B.
C. D.(1,e)
解析 因为f′(x)==,
∴f(x)在(-∞,1)上单调递增,在(1,+∞)上单调递减.
因此f(x)max=f(1)=.
又当x→-∞时,f(x)→-∞;
当x→+∞时,f(x)→0且f(x)>0,又f(0)=0,
从而作出t=f(x)的简图,如图所示.
令t=f(x),g(t)=t2+mt+m-1.
由g(t)=0,得t=-1或t=1-m.
当t=-1时,f(x)==-1,方程有一解.
要使原方程有3个不同的实数解,必须t=1-m与t=f(x)的图象有两个交点.
故0<1-m<,所以1-b,则( )
A.ln(a-b)>0 B.3a<3b
C.a3-b3>0 D.|a|>|b|
解析 法一 不妨设a=-1,b=-2,则a>b,可验证A,B,D错误,只有C正确.
法二 由a>b,得a-b>0.但a-b>1不一定成立,
则ln(a-b)>0不一定成立,故A不一定成立.
因为y=3x在R上是增函数,当a>b时,3a>3b,故B不成立.
因为y=x3在R上是增函数,当a>b时,a3>b3,即a3-b3>0,故C成立.
因为当a=3,b=-6时,a>b,但|a|<|b|,D项不正确.
答案 C
4.定义在R上的奇函数f(x)满足f(1-x)=f(1+x),当x∈[0,1]时,f(x)=4x2-2x,则当x∈[-3,3]时,方程2f(x)=1的解的个数为( )
A.3 B.4 C.6 D.8
解析 f(x)在R上为奇函数,知f(x)的图象关于原点对称.
又f(1-x)=f(1+x),∴y=f(x)的图象关于直线x=1对称.
由题设,作出函数y=f(x)的大致图象(如图).
∴y=f(x),x∈[-3,3]的图象与直线y=有三个交点.
故方程2f(x)=1有3个解.
答案 A
5.已知函数f(x)=(ex+e-x)ln -1,若f(a)=1,则f(-a)=( )
A.1 B.-1 C.3 D.-3
解析 设g(x)=f(x)+1=(ex+e-x)ln .
易知g(-x)=(e-x+ex)ln =-g(x).
由f(a)=1,得g(a)=2.
∴g(-a)=-2,从而f(-a)=g(-a)-1=-3.
答案 D
6.函数f(x)=xa满足f(2)=4,那么函数g(x)=|loga(x+1)|的图象大致为( )
解析 由函数f(x)=xa满足f(2)=4,知2a=4,
所以a=2,f(x)=x2,则g(x)=|log2(x+1)|,
将函数h(x)=log2x的图象向左平移1个单位长度(纵坐标不变),然后将x轴下方的图象折上去,即可知选C.
答案 C
7.已知函数f(x)=|2x-1|,af(c)>f(b),则下列结论中,一定成立的是( )
A.a<0,b<0,c<0 B.a<0,b≥0,c>0
C.2-a<2c D.2a+2c<2
解析 作出函数f(x)=|2x-1|的图象,如图,
∵af(c)>f(b),
结合图象知,
00,
∴0<2a<1.
∴f(a)=|2a-1|=1-2a<1,
∴f(c)<1,∴0f(c),
∴1-2a>2c-1,
∴2a+2c<2,故选D.
答案 D
8.若函数f(x)=的图象如图所示,则m的取值范围为( )
A.(-∞,-1)
B.(-1,2)
C.(0,2)
D.(1,2)
解析 由图可知,f(x)的定义域为R,所以m>0.
又因为x→+∞时,f(x)>0,所以2-m>0⇒m<2.
又因为f(x)是奇函数,所以x>0时,
f(x)==,
所以f(x)在(0,)上单调递增,(,+∞)上单调递减,所以>1⇒m>1,
综上,实数m的取值范围是(1,2).
答案 D
二、填空题
9.已知函数f(x)=若f(2-a)=1,则f(a)=________.
解析 当2-a<2,即a>0时,f(2-a)=-log2(1+a)=1.
解得a=-,不合题意.
当2-a≥2,即a≤0时,f(2-a)=2-a-1=1,即2-a=2,解得a=-1,所以f(a)=f(-1)=-log24=-2.
答案 -2
10.若函数f(x)=loga(x>0,a>0且a≠1)的值域为R,则实数a的取值范围是________________.
解析 设g(x)=x+-4(x>0),
又函数f(x)=loga(a>0且a≠1)的值域为R,
∴x+-4≤0必有解,故函数g(x)的最小值必须要小于等于零,又g(x)≥2-4,
当且仅当x=时,等号成立.
要满足题意,需2-4≤0,解得a≤4.
故实数a的取值范围是(0,1)∪(1,4].
答案 (0,1)∪(1,4]
11.(2020·郑州质量预测)已知函数f(x)=若不等式f(x)≤5-mx恒成立,则实数m的取值范围是________.
解析 如图,在同一平面直角坐标系内作出y=f(x)和y=-mx+5的图象,直线y=5-mx过定点A(0,5),当直线y=-mx+5位于平行于x轴的位置和直线AB之间时,满足不等式f(x)≤5-mx恒成立,所以≤-m≤0,解得0≤m≤.
答案
12.(2020·南昌调研)若对任意的t∈[1,2],函数f(x)=t2x2-(t+1)x+a总有零点,则实数a的取值范围是________.
解析 由题意得(t+1)2-4at2≥0对t∈[1,2]恒成立,
所以4at2≤(t+1)2对t∈[1,2]恒成立,
则a≤对t∈[1,2]恒成立,
设y=,则y′=-<0,
故函数y=在t∈[1,2]上单调递减,
∴ymin==.
∴的最小值为,故a≤.
答案
B级 能力提升
13.函数f(x)=,若a=f,b=f(ln 2),c=f,则有( )
A.c>b>a B.b>a>c
C.c>a>b D.b>c>a
解析 f(x)===1+,
∴f(x)在(-∞,0),(0,+∞)上为减函数,
易知x<0时,f(x)<0,x>0时,f(x)>0,
又∵ln 2>0,-<0,ln <0,∴b>0,a<0,c<0.
又-=-ln ,ln =-ln 3,且-ln >-ln 3,
∴->ln ,∵f(x)在(-∞,0)上单调递减,
∴fa,∴b>c>a.
答案 D
14.已知函数f(x)=则函数y=f(e-x)的大致图象是( )
解析 令g(x)=f(e-x),则g(x)=
即g(x)=
因此g(x)在(0,+∞),(-∞,0)上都是减函数,排除A,C;
又ee-0>ln(e-0)=1,排除D,因而B项成立.
答案 B
15.若函数f(x)=有且只有2个不同的零点,则实数k的取值范围是( )
A.(-4,0) B.(-∞,0]
C.(-4,0] D.(-∞,0)
解析 x>0时,x=1为f(x)的零点,x≤0时,x=0为f(x)的零点,故x<0时,f(x)不能再有其它零点,即方程=kx2(x<0)无解,等价于=kx(x<0)无解.
作出y=(x<0),y=kx(x<0)的图象如图.
当k>0时,y=kx与y=相交.
∴k≤0时,y=kx与y=不相交.
此时f(x)仅有两个零点x=0与x=1.
答案 B
16.(2018·全国Ⅰ卷改编)已知函数f(x)=
g(x)=f(x)+x+a.若g(x)存在2个零点,则a的取值范围是________.
解析 依题意,g(x)=f(x)+x+a=0有两个实根,
∴关于x的方程f(x)=-x-a有两个实根.
作出f(x)=与y=-x-a的图象.
根据图象知,当-a≤1时,即a≥-1时,两图象有两个交点.
故实数a的取值范围是[-1,+∞).
答案 [-1,+∞)
C级 创新猜想
17.(多选题)(2020·烟台调研)已知函数f(x)=ln x+ln(4-x),则下列四个命题正确的是( )
A.f(x)在(0,2)上单调递增
B.f(x)在(0,4)上单调递增
C.f(x)的图象关于直线x=2对称
D.f(x)的图象上存在两点关于点(2,0)对称
解析 f(x)=ln x+ln(4-x)=ln x(4-x)
=ln[4-(x-2)2],x∈(0,4).
设z=4-(x-2)2,x∈(0,4),
由于z=4-(x-2)2在(0,2)上单调递增,在(2,4)上单调递减,
y=ln z在(0,+∞)上单调递增.
∴f(x)在(0,2)上单调递增,在(2,4)上单调递减,故A正确,B错误.
又f(2+x)=ln(4-x2)为偶函数,其图象关于x=0对称,f(x)由f(x+2)的图象向右平移两个单位得到,所以f(x)的图象关于x=2对称,故C正确.
由f(2+x)+f(2-x)=2ln(2-x)+2ln(2+x)=0,得x=±,
∴f(x)的图象上存在两点(2-,0),(2+,0)关于点(2,0)对称,D正确.故选ACD.
答案 ACD
相关文档
- 高中数学第7章三角函数课时分层作2021-06-165页
- 高中数学第二章函数第4节二次函数2021-06-166页
- 高中数学人教a版选修2-2(课时训练):3.2021-06-168页
- 人教a版高中数学选修1-1:综合质量评2021-06-168页
- 高中数学人教a版必修五第二章数列2021-06-165页
- 高中数学公式大全完整版(供参考)2021-06-168页
- 眉山市高中 2018届第三学期期末2021-06-165页
- 高中人教a版数学必修1单元测试:创优2021-06-1613页
- 高中数学人教a版选修4-1课时跟踪检2021-06-164页
- 高中数学人教B版必修三第二章统计22021-06-165页