2020-2021学年人教A版数学选修2-1课时作业：第三章　空间向量与立体几何 单元质量评估（一） 17页

第三章单元质量评估(一) 时限：120 分钟 满分：150 分 一、选择题(本大题共 12 小题，每小题 5 分，共 60 分，在每小 题给出的四个选项中，只有一项是符合要求的) 1．在长方体 ABCDA1B1C1D1 中，AB → ＋BC → ＋CC1 → －D1C1 → 等于 ( A ) A.AD1 → B.AC1 → C.AD → D.AB → 2．已知 a＝3i＋2j－k，b＝i－j＋2k，则 5a 与 3b 的数量积等于 ( A ) A．－15 B．－5 C．－3 D．－1 3．已知 a＝(2，－1,3)，b＝(－1,4，－2)，c＝(7,5，λ)，若 a，b， c 三向量共面，则实数λ等于( D ) A.62 7 B．9 C.60 7 D.65 7 解析：本题考查向量共面．∵a，b，c 三向量共面，∴存在实数 m，n，使得 c＝ma＋nb，即 7＝2m－n 5＝－m＋4n λ＝3m－2n ，∴λ＝65 7 .故选 D. 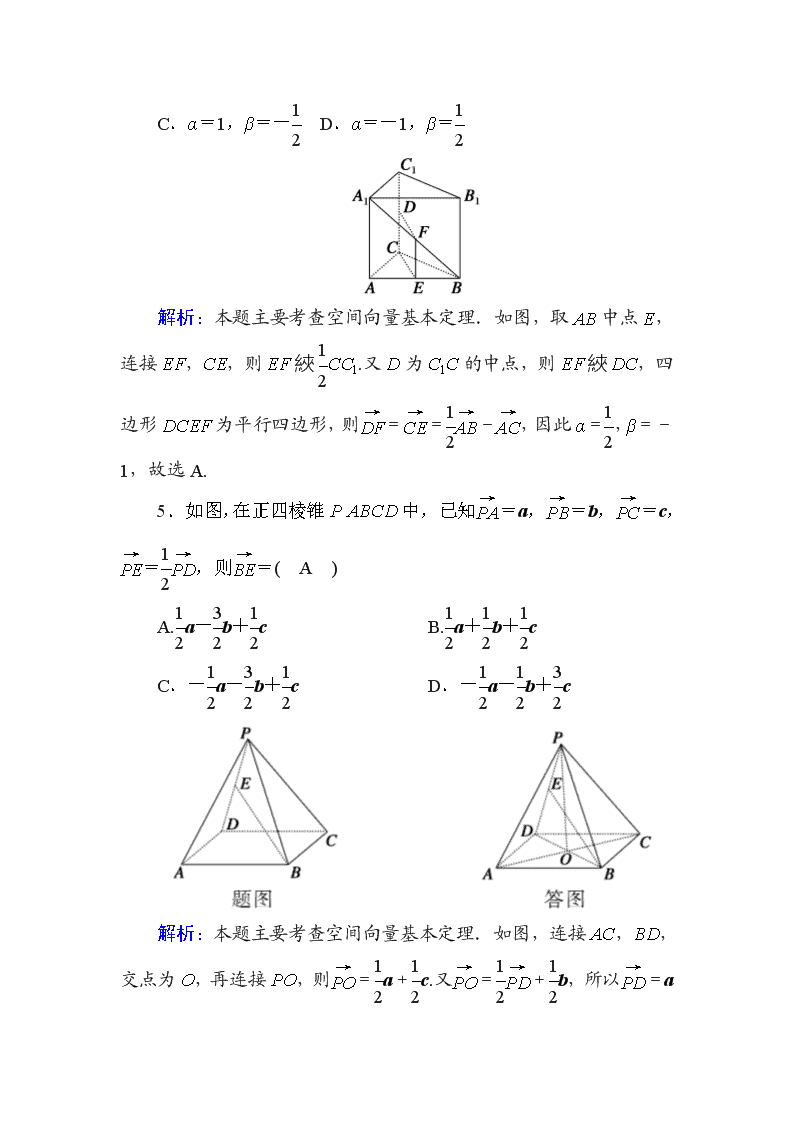4．在三棱柱 ABCA1B1C1 中，D，F 分别是 CC1，A1B 的中点， 且DF → ＝αAB →＋βAC →，则( A ) A．α＝1 2 ，β＝－1 B．α＝－1 2 ，β＝1 C．α＝1，β＝－1 2 D．α＝－1，β＝1 2 解析：本题主要考查空间向量基本定理．如图，取 AB 中点 E， 连接 EF，CE，则 EF 綊 1 2CC1.又 D 为 C1C 的中点，则 EF 綊 DC，四 边形 DCEF 为平行四边形，则DF → ＝CE → ＝1 2AB →－AC → ，因此α＝1 2 ，β＝ －1，故选 A. 5．如图，在正四棱锥 PABCD 中，已知PA →＝a，PB →＝b，PC →＝c， PE →＝1 2PD → ，则BE →＝( A ) A.1 2a－3 2b＋1 2c B.1 2a＋1 2b＋1 2c C．－1 2a－3 2b＋1 2c D．－1 2a－1 2b＋3 2c 解析：本题主要考查空间向量基本定理．如图，连接 AC，BD， 交点为 O，再连接 PO，则PO → ＝1 2a＋1 2c.又PO → ＝1 2PD → ＋1 2b，所以PD → ＝a ＋c－b，故PE →＝1 2PD → ＝1 2a＋1 2c－1 2b，从而BE →＝BP →＋PE →＝1 2a－3 2b＋1 2c， 故选 A. 6．如图，在平行六面体 ABCDA1B1C1D1 中，M 在 AC 上，且 AM ＝1 2MC，N 在 A1D 上，且 A1N＝2ND.设AB →＝a，AD → ＝b，AA1 → ＝c，则MN → ＝( A ) A．－1 3a＋1 3b＋1 3c B．a＋1 3b－1 3c C.1 3a－1 3b－2 3c D．－1 3a＋b＋1 3c 解析：因为 M 在 AC 上，且 AM＝1 2MC，N 在 A1D 上，且 A1N＝ 2ND，所以AM → ＝1 3AC →，A1N → ＝2 3A1D → .又 ABCDA1B1C1D1 为平行六面体， 且AB →＝a，AD → ＝b，AA1 → ＝c，所以AC →＝a＋b，A1D → ＝b－c，所以MN → ＝ MA → ＋AA1 → ＋A1N → ＝－1 3AC → ＋AA1 → ＋2 3A1D → ＝－1 3(a＋b)＋c＋2 3(b－c)＝－ 1 3a＋1 3b＋1 3c. 7．将正方形 ABCD 沿对角线 BD 折成直二面角 ABDC，则下列 结论错误的是( C ) A．AC⊥BD B．△ACD 是等边三角形 C．AB 与平面 BCD 所成的角为 90° D．AB 与 CD 所成的角为 60° 解析：如图，取 BD 的中点 O，连接 AO，CO，AC，则 AO⊥BD， CO⊥BD.又 AO∩CO＝O，∴BD⊥平面 AOC，又 AC⊂平面 AOC，∴ AC⊥BD，A 中结论正确；∵AC＝ 2AO＝AD＝CD，∴△ACD 是等 边三角形，B 中结论正确；∵AO⊥平面 BCD，∴∠ABD 是 AB 与平 面 BCD 所成的角，为 45°，C 中结论错误；AC → ＝AB →＋BD → ＋DC → ，不 妨设 AB＝1，则 AC → 2＝(AB →＋BD → ＋DC → )2＝AB → 2＋BD → 2＋DC → 2＋2AB → ·BD → ＋ 2BD → ·DC → ＋2AB → ·DC → ，∴1＝1＋2＋1＋2 2× － 2 2 ＋2 2× － 2 2 ＋ 2cos〈AB →，DC → 〉，∴cos〈AB →，DC → 〉＝1 2 ，∴〈AB →，DC → 〉＝60°，即 AB 与 CD 所成的角为 60°，D 中结论正确．故选 C. 8.如图所示，正方体 ABCDA1B1C1D1 的棱长为 a，M，N 分别为 A1B 和 AC 上的点，且 A1M＝AN＝ 2 3 a，则 MN 与平面 BB1C1C 的位 置关系是( B ) A．斜交 B．平行 C．垂直 D．不能确定 解析：设A1A → ＝a，A1B1 → ＝b，A1D1 → ＝c.由题意，知 A1B＝AC＝ 2a. 又 A1M＝AN＝ 2 3 a，∴A1M → ＝1 3A1B → ＝1 3(a＋b)，AN →＝1 3AC →＝1 3(b＋c)，则 MN → ＝A1A → ＋AN →－A1M → ＝a＋1 3(b＋c)－1 3(a＋b)＝2 3a＋1 3c，因此，MN → 与 A1A → ，A1D1 → 共面，∴MN∥平面 AA1D1D，从而 MN∥平面 BB1C1C. 9.如图，在直三棱柱 ABCA1B1C1 中，∠ACB＝90°，2AC＝AA1 ＝BC＝2，D 为 AA1 上一点．若二面角 B1DCC1 的大小为 60°，则 AD 的长为( A ) A. 2 B. 3 C．2 D. 2 2 解析：本题考查空间向量在立体几何中的应用．如图，以 C 为 坐标原点，CA，CB，CC1 所在的直线分别为 x 轴、y 轴、z 轴建立空 间直角坐标系，则 C(0,0,0)，B1(0,2,2)．设 AD＝a，则点 D 的坐标为(1,0， a)，CD → ＝(1,0，a)，CB1 → ＝(0,2,2)．设平面 B1CD 的一个法向量为 m＝ (x，y，z)， 则 m·CB1 → ＝0， m·CD → ＝0 ⇒ 2y＋2z＝0， x＋az＝0， 令 z＝－1，得 m＝(a,1，－ 1)．又平面 C1DC 的一个法向量为(0,1,0)，记为 n，则由 cos60°＝ m·n |m||n| ， 得 1 a2＋2 ＝1 2 ，即 a＝ 2，故 AD＝ 2.故选 A. 10．设 P 是 60°的二面角αlβ内一点，PA⊥α，PB⊥β，A，B 是 垂足，PA＝4，PB＝2，则 AB 的长度为( D ) A．2 2 B．2 3 C．2 5 D．2 7 解析：本题主要考查空间向量的模的求解方法，考查空间向量的 数量积运算．由已知，得〈PA →，PB →〉＝120°，AB →＝PB →－PA →，|AB → |2＝|PB → －PA → |2＝|PA → |2＋|PB → |2－2|PA → ||PB → |cos〈PA →，PB →〉＝28，则|AB → |＝2 7，故 选 D. 11．三棱柱 ABCA1B1C1 中，底面 ABC 为正三角形，侧棱长等于 底面边长，A1 在底面的射影是△ABC 的中心，则 AB1 与底面 ABC 所 成角的正弦值等于( B ) A.1 3 B. 2 3 C. 3 3 D.2 3 解析：如图，设 A1 在底面 ABC 内的射影为 O，以 O 为坐标原点， 建立如图所示的空间直角坐标系． 设△ABC 边长为 1，则 A 3 3 ，0，0 ，B1 － 3 2 ，1 2 ， 6 3 ，所以AB1 → ＝ －5 3 6 ，1 2 ， 6 3 . 平面 ABC 的法向量 n＝(0,0,1)， 则 AB1 与底面 ABC 所成角α的正弦值为 sinα＝|cos〈AB1 → ，n〉|＝ 6 3 75 36 ＋1 4 ＋6 9 ＝ 2 3 .故选 B. 12．在三棱锥 PABC 中，△ABC 为等边三角形，PA⊥平面 ABC， 且 PA＝AB，则二面角 APBC 的平面角的正切值为( A ) A. 6 B. 3 C. 6 6 D. 6 2 解析：设 PA＝AB＝2，建立如图所示的空间直角坐标系． 则 B(0,2,0)，C( 3，1,0)，P(0,0,2)．所以BP →＝(0，－2,2)，BC →＝( 3， －1,0)． 设 n＝(x，y，z)是平面 PBC 的一个法向量．则 BP → ·n＝0， BC → ·n＝0， 即 －2y＋2z＝0， 3x－y＝0. 令 y＝1.则 x＝ 3 3 ，z＝1.即 n＝ 3 3 ，1，1 .易知 m＝(1,0,0)是平面 PAB 的一个法向量． 则 cos〈m，n〉＝ m·n |m||n| ＝ 3 3 1× 21 3 ＝ 7 7 .所以正切值 tan〈m，n〉 ＝ 6.故选 A. 二、填空题(本大题共 4 小题，每小题 5 分，共 20 分，请把答案 填写在题中横线上) 13．已知 a＝(3λ，6，λ＋6)，b＝(λ＋1,3,2λ)为两平行平面的法向 量，则λ＝2. 解析：由题意知 a∥b，所以 3λ λ＋1 ＝6 3 ＝λ＋6 2λ ，解得λ＝2. 14.如图，在平行六面体 ABCDA1B1C1D1 中，E 为底面正方形 ABCD 的中心，设A1E → ＝A1A → ＋xA1B1 → ＋yA1D1 → ，则 x＋y＝1. 解析：本题主要考查空间向量基本定理.A1E → ＝A1B → ＋A1D → 2 ＝ A1A → ＋AB →＋A1A → ＋AD →  2 ＝A1A → ＋AB →＋AD → 2 ＝A1A → ＋A1B1 → ＋A1D1 → 2 ，因而 x ＝y＝1 2 ，所以 x＋y＝1. 15．空间四点 A(2,3,1)，B(4,1,2)，C(6,3,7)，D(3,1,0)，则点 D 到 平面 ABC 的距离是 17 17 . 解析：本题主要考查空间向量的坐标运算以及空间点到平面的距 离的求法．由已知，得AB →＝(2，－2,1)，AC →＝(4,0,6)．设平面 ABC 的 法向量为 n＝(x，y，z)，则 AB → ·n＝0， AC → ·n＝0， 即 2x－2y＋z＝0， 4x＋6z＝0， 令 x ＝3，则 y＝2，z＝－2，所以 n＝(3,2，－2)，AD → ＝(1，－2，－1)， 所以点 D 到平面 ABC 的距离为|AD → ·n| |n| ＝ 17 17 . 16．在四棱锥 PABCD 中，PD⊥底面 ABCD，底面 ABCD 是正 方形，且 PD＝AB＝1，G 为△ABC 的重心，则 PG 与底面 ABCD 所 成的角θ的正弦值为3 17 17 . 解析：本题主要考查向量法求线面角，考查三角形重心的坐标公 式．如图，分别以 DA，DC，DP 所在直线为 x 轴、y 轴、z 轴建立空 间直角坐标系，由已知 D(0,0,0)，P(0,0,1)，A(1,0,0)，B(1,1,0)，C(0,1,0)， 则重心 G 2 3 ，2 3 ，0 ，因而DP → ＝(0,0,1)，GP → ＝ －2 3 ，－2 3 ，1 ，那么 sinθ ＝|cos〈DP → ，GP → 〉|＝ |DP → ·GP → | |DP → |·|GP → | ＝3 17 17 . 三、解答题(本大题共 6 小题，共 70 分．解答应写出文字说明， 证明过程或演算步骤) 17．(10 分)如图，正方体 ABCDA′B′C′D′中，点 E 是上底 面 A′B′C′D′的中心，用向量DA → ，DC → ，DD′→ 表示向量BD′→ ，AE → . 解：BD′→ ＝DD′→ －DB → ＝－DA → －DC → ＋DD′→ . AE → ＝AA′→ ＋A′E → ＝DD′→ ＋1 2A′C′→ ＝DD′→ ＋1 2AC → ＝DD′→ ＋ 1 2(DC → －DA → )＝－1 2DA → ＋1 2DC → ＋DD′→ . 18．(12 分)如图，在四棱锥 PABCD 中，底面 ABCD 是平行四边 形，PG⊥平面 ABCD，垂足为 G，G 在 AD 上，且 PG＝4，AG＝1 3GD， BG⊥GC，GB＝GC＝2，E 是 BC 的中点． (1)求异面直线 GE 与 PC 所成角的余弦值； (2)若 F 是棱 PC 上一点，且 DF⊥GC，求PF FC 的值． 解：(1)以 G 点为坐标原点，分别以GB → ，GC → ，GP → 的方向为 x 轴、 y 轴、z 轴的正方向建立空间直角坐标系，则 G(0,0,0)，B(2,0,0)， C(0,2,0)，P(0,0,4)，故 E(1,1,0)，GE → ＝(1,1,0)，PC →＝(0,2，－4)． ∵cos〈GE → ，PC →〉＝ GE → ·PC → |GE → ||PC → | ＝ 2 2× 20 ＝ 10 10 ，∴GE 与 PC 所成 角的余弦值为 10 10 . (2)∵GD → ＝3 4BC →＝ －3 2 ，3 2 ，0 ，∴D －3 2 ，3 2 ，0 . 设 F(0，y，z)，则DF → ＝(0，y，z)－ －3 2 ，3 2 ，0 ＝ 3 2 ，y－3 2 ，z . ∵DF → ⊥GC → ，∴DF → ·GC → ＝0，即 3 2 ，y－3 2 ，z ·(0,2,0)＝2y－3＝0， ∴y＝3 2. 又点 F 在 PC 上，∴PF →＝λPC → ，即 0，3 2 ，z－4 ＝λ(0,2，－4)， ∴z＝1，故 F 0，3 2 ，1 ， ∴PF →＝ 0，3 2 ，－3 ，FC →＝ 0，1 2 ，－1 ，∴PF FC ＝ 3 5 2 5 2 ＝3. 19．(12 分)如图，在多面体 EFABCD 中，正方形 ADEF 与梯形 ABCD 所在平面互相垂直，AB∥CD，AD⊥CD，AB＝AD＝1，CD＝2， M，N 分别为 EC 和 BD 的中点． (1)求证：BC⊥平面 BDE； (2)求直线 MN 与平面 BMC 所成角的正弦值． 解：(1)证明：如图，在梯形 ABCD 中，取 CD 的中点 H，连接 BH. 因为 AD＝AB，AB∥CD，AD⊥CD，AB＝1，CD＝2，所以四边 形 ADHB 为正方形． 又 BD2＝AD2＋AB2＝2，BC2＝HC2＋HB2＝2，所以 CD2＝BD2＋ BC2，所以 BC⊥BD. Z 又平面 ADEF⊥平面 ABCD，平面 ADEF∩平面 ABCD＝AD， DE⊥AD， 所以 DE⊥平面 ABCD，所以 BC⊥DE.又 BD∩DE＝D，故 BC⊥ 平面 BDE. (2)由(1)，知 DE⊥平面 ABCD，AD⊥CD，所以 DE，DA，DC 两 两垂直． 以 D 为坐标原点，建立如图所示的空间直角坐标系 Dxyz， 则 C(0,2,0)，B(1,1,0)，M 0，1，1 2 ，N 1 2 ，1 2 ，0 ，所以BC → ＝(－ 1,1,0)，MC → ＝ 0，1，－1 2 . 设 n＝(x，y，z)为平面 BMC 的法向量，则 n·BC →＝0 n·MC → ＝0 ，即 －x＋y＝0 y－1 2z＝0 ，可取 n＝(1,1,2)． 又 M N →＝ 1 2 ，－1 2 ，－1 2 ，所以 cos〈n，MN → 〉＝ n·MN → |n||MN → | ＝－ 2 3 ， 所以直线 MN 与平面 BMC 所成角的正弦值为 2 3 . 20．(12 分)如图，在四棱锥 SABCD 中，底面 ABCD 是直角梯形， 侧棱 SA⊥底面 ABCD，AB 垂直于 AD 和 BC，SA＝AB＝BC＝2，AD ＝1，M 是棱 SB 的中点． (1)求证：AM∥平面 SCD； (2)求平面 SCD 与平面 SAB 所成的二面角的余弦值； (3)设点 N 是线段 CD 上的动点，MN 与平面 SAB 所成的角为θ， 求 sinθ的最大值． 解：(1)证明：以点 A 为坐标原点，建立如图所示的空间直角坐 标系， 则 A(0,0,0)，B(0,2,0)，C(2,2,0)，D(1,0,0)，S(0,0,2)，M(0,1,1)， ∴AM → ＝(0,1,1)，SD →＝(1,0，－2)，CD → ＝(－1，－2,0)， 设平面 SCD 的法向量为 n＝(x，y，z)，则 SD → ·n＝0 CD → ·n＝0 ，∴ x－2z＝0 －x－2y＝0 ， 令 z＝1，得 n＝(2，－1,1)． ∵AM → ·n＝0，∴AM → ⊥n，∴AM∥平面 SCD. (2)易知平面 SAB 的一个法向量为 n1＝(1,0,0)， 设平面 SCD 与平面 SAB 所成的二面角为φ，易知 0°<φ≤90°， 则 cosφ＝| n·n1 |n||n1||＝ 2 6×1 ＝ 6 3 ，∴平面 SCD 与平面 SAB 所成的 二面角的余弦值为 6 3 . (3)设 N(x,2x－2,0)(1≤x≤2)，则MN → ＝(x,2x－3，－1)，平面 SAB 的一个法向量为 n1＝(1,0,0)， ∴sinθ＝| n1·MN → |n1||MN → ||＝| x 5x2－12x＋10|＝ 1 10× 1 x 2－12×1 x ＋5 ＝ 1 10 1 x －3 5 2＋7 5 ， ∴当1 x ＝3 5 ，即 x＝5 3 时，sinθ取得最大值，最大值为 35 7 . 21．(12 分)如图①在直角梯形 ABCP 中，BC∥AP，AB⊥BC，CD ⊥AP，AD＝DC＝PD＝2，E，F，G 分别是线段 PC，PD，BC 的中 点，现将△PDC 折起，使平面 PDC⊥平面 ABCD.(如图②) (1)求证：AP∥平面 EFG； (2)求二面角 GEFD 的大小． 解：(1)证明：因为在图①中，AP⊥CD，所以在图②中 PD⊥CD， AD⊥CD，所以∠ADP 是二面角 PDCA 的平面角， 因为平面 PDC⊥平面 ABCD，所以∠ADP＝90°，即 PD⊥DA， 又 AD∩DC＝D，所以 PD⊥平面 ABCD. 如图．以 D 为坐标原点，直线 DA，DC，DP 分别为 x，y 与 z 轴建立空间直角坐标系，则 D(0,0,0)，A(2,0,0)，B(2,2,0)，C(0,2,0)， P(0,0,2)，E(0,1,1)，F(0,0,1)，G(1,2,0)． 所以AP →＝(－2,0,2)，EF →＝(0，－1,0)，FG → ＝(1,2，－1)， 设平 面 GEF 的法 向量 n ＝(x， y， z)，由 法向量 的定义 得 n·EF →＝0， n·FG → ＝0 ⇒ x，y，z·0，－1，0＝0， x，y，z·1，2，－1＝0 ⇒ y＝0， x＋2y－z＝0 ⇒ y＝0， x＝z. 不妨设 z＝1，则 n＝(1,0,1)，AP → ·n＝－2×1＋2×0＋1×2＝0， 所以AP →⊥n，点 P∉平面 EFG，所以 AP∥平面 EFG. (2)由(1)知平面 GEF 的法向量 n＝(1,0,1)，因平面 EFD 与坐标平 面 PDC 重合，则它的一个法向量为 i＝(1,0,0)， 由图形观察二面角 GEFD 为锐角，设二面角 GEFD 为θ，则 cosθ＝|n·i| |n| ＝ 1 2 ＝ 2 2 . 故二面角 GEFD 的大小为 45°. 22．(12 分)如图，在△ABC 中，∠C＝90°，AC＝BC＝a，点 P 在 AB 上，PE∥BC 交 AC 于点 E，PF∥AC 交 BC 于点 F.沿 PE 将△ APE 翻折成△A′PE，使平面 A′PE⊥平面 FCEP，沿 PF 将△BPF 翻折成△B′PF，使平面 B′PF⊥平面 FCEP. (1)求证：B′C∥平面 A′PE； (2)设AP PB ＝λ，当λ为何值时，二面角 CA′B′P 的大小为 60°？ 解：(1)证明：因为 FC∥PE，FC⊄平面 A′PE，所以 FC∥平面 A′EP.因为平面 A′PE⊥平面 FCEP，且 A′E⊥PE，所以 A′E⊥平 面 FCEP.同理，B′F⊥平面 FCEP，所以 B′F∥A′E，从而 B′F ∥平面 A′PE. 又 FC∩B′F＝F，所以平面 B′CF∥平面 A′PE，从而 B′C ∥平面 A′PE. (2)以点 C 为坐标原点，CF 所在直线为 x 轴，CE 所在直线为 y 轴，过 C 且垂直于平面 FCEP 的直线为 z 轴，建立空间直角坐标系， 如图， 则 C(0,0,0) ， A′ 0， a λ＋1 ， λa λ＋1 ， B′ λa λ＋1 ，0， a λ＋1 ， P λa λ＋1 ， a λ＋1 ，0 ， ∴CA′→ ＝ 0， a λ＋1 ， λa λ＋1 ，A′B′→ ＝ λa λ＋1 ，－ a λ＋1 ，1－λa λ＋1 ， B′P → ＝ 0， a λ＋1 ，－ a λ＋1 ， ∴平面 CA′B′的一个法向量为 m＝ 1 λ ，λ，－1 ，平面 PA′B′ 的一个法向量为 n＝(1,1,1)． 由|m·n| |m||n| ＝ |1 λ ＋λ－1| 1 λ2＋λ2＋1· 3 ＝cos60°＝1 2 ，化简得1 λ2＋λ2－8 λ －8λ＋9 ＝0，解得λ＝7±3 5 2 .