高中数学第二讲参数方程四渐开线与摆线互动课堂学案新人教A版选修4-41 4页

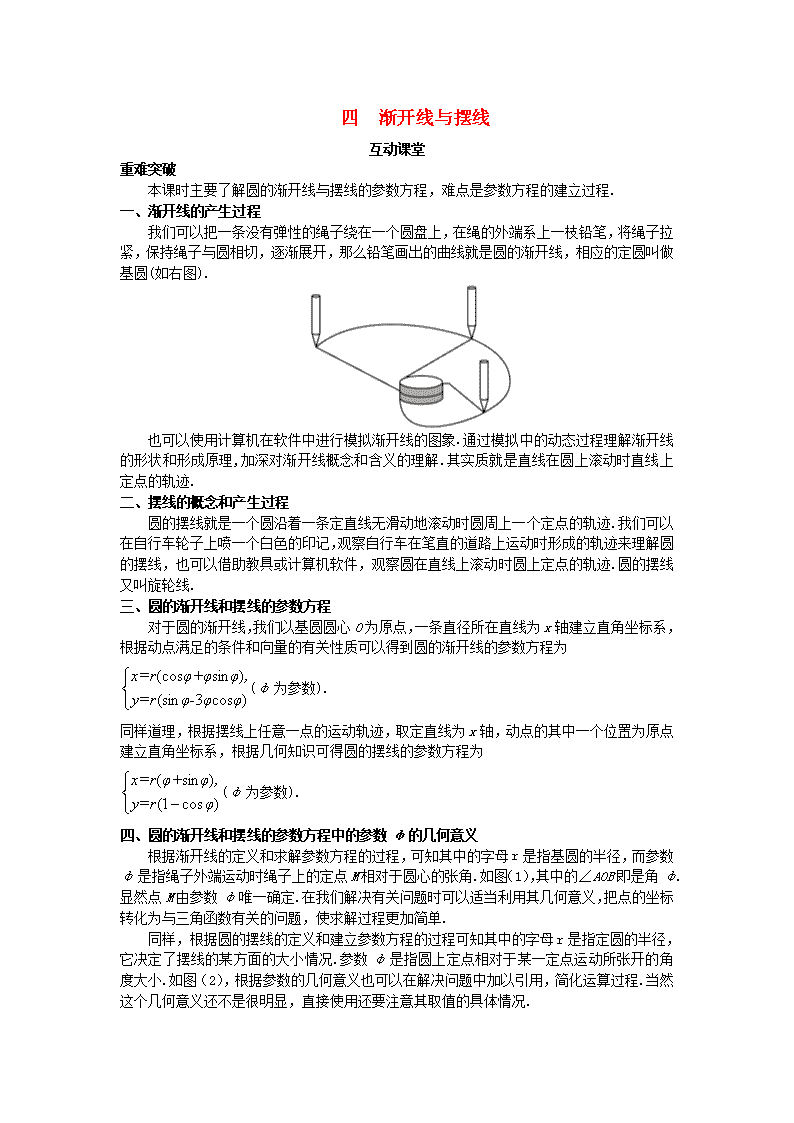
四 渐开线与摆线 互动课堂 重难突破 本课时主要了解圆的渐开线与摆线的参数方程，难点是参数方程的建立过程. 一、渐开线的产生过程 我们可以把一条没有弹性的绳子绕在一个圆盘上，在绳的外端系上一枝铅笔，将绳子拉 紧，保持绳子与圆相切，逐渐展开，那么铅笔画出的曲线就是圆的渐开线，相应的定圆叫做 基圆(如右图). 也可以使用计算机在软件中进行模拟渐开线的图象.通过模拟中的动态过程理解渐开线 的形状和形成原理,加深对渐开线概念和含义的理解.其实质就是直线在圆上滚动时直线上 定点的轨迹. 二、摆线的概念和产生过程 圆的摆线就是一个圆沿着一条定直线无滑动地滚动时圆周上一个定点的轨迹.我们可以 在自行车轮子上喷一个白色的印记，观察自行车在笔直的道路上运动时形成的轨迹来理解圆 的摆线，也可以借助教具或计算机软件，观察圆在直线上滚动时圆上定点的轨迹.圆的摆线 又叫旋轮线. 三、圆的渐开线和摆线的参数方程 对于圆的渐开线，我们以基圆圆心 O 为原点，一条直径所在直线为 x 轴建立直角坐标系， 根据动点满足的条件和向量的有关性质可以得到圆的渐开线的参数方程为    )cos3sin( )sincos( φφφ-y=r ,φφ+φx=r (φ为参数). 同样道理，根据摆线上任意一点的运动轨迹，取定直线为 x 轴，动点的其中一个位置为原点 建立直角坐标系，根据几何知识可得圆的摆线的参数方程为     )cos1( )sin( φy=r ,φφ+x=r (φ为参数). 四、圆的渐开线和摆线的参数方程中的参数φ的几何意义 根据渐开线的定义和求解参数方程的过程，可知其中的字母 r 是指基圆的半径，而参数 φ是指绳子外端运动时绳子上的定点 M 相对于圆心的张角.如图（1），其中的∠AOB 即是角 φ.显然点 M 由参数φ唯一确定.在我们解决有关问题时可以适当利用其几何意义，把点的坐 标转化为与三角函数有关的问题，使求解过程更加简单. 同样，根据圆的摆线的定义和建立参数方程的过程可知其中的字母 r 是指定圆的半径， 它决定了摆线的某方面的大小情况.参数φ是指圆上定点相对于某一定点运动所张开的角度 大小.如图（2），根据参数的几何意义也可以在解决问题中加以引用，简化运算过程.当然这 个几何意义还不是很明显，直接使用还要注意其取值的具体情况. (1) (2) 五、用参数方程描述运动规律的特点 有些重要但较复杂的曲线(例如圆的渐开线)，建立它们的普通方程比较困难，甚至不可 能，列出的方程既复杂又不易理解，从普通方程看不出曲线的坐标所满足条件的含义.如圆 的渐开线的普通方程，可以根据其参数方程      )cos(sin )sin(cos φφφy=r ,φφφx=r (φ为参数)消去参数φ得 到 .)1sin()1cos( 222222 rryxryryxrr  根据方程画出曲线十分费时，而利用参数方程把两个变量 x、y 间接地联系起来，常常 比较容易，方程简单明确，且画图也不太困难.对于参数方程，我们可以根据参数的取值求 出坐标的关系，相比之下比普通方程更为直观.所以，在研究圆的渐开线和圆的摆线时主要 使用参数方程，而不去讨论其普通方程. 活学巧用 【例 1】写出半径为 2 的基圆的渐开线方程. 解:半径为 2 的基圆的渐开线方程    )cos3sin(2 )sincos(2 φφφ-y= ,φφ+φx= (φ为参数). 【例 2】求摆线      )cos1(2 )sin(2 ty= ,ttx= (0≤t≤2π)与直线 y=2 的交点的直角坐标. 解:y=2 时，2=2（1-cost）,∴cost=0. ∵0≤t≤2π,∴t= 2 π 或 2 3 π. ∴x1=2( 2 π -sin 2 π )=π-2,x2=2( 2 3 π-sin 2 3 π)=3π+2. ∴交点的直角坐标为（π-2，2），（3π+2，2）. 【例 3】已知一个圆的摆线过一定点（1，0）,请写出该摆线的参数方程. 解析:根据圆的摆线的参数方程的表达式      )cos1( )sin( φy=r ,φφx=r (φ为参数),可知只需求出其中 的 r，也就是说，摆线的参数方程由圆的半径唯一确定，因此只需把点(1，0)代入参数方程 求出 r 值再代入参数方程的表达式. 解:令 r(1-cosφ)=0,可得 cosφ=1. 所以φ=2kπ(k∈Z)代入可得 x=r(2kπ-sin2kπ)=1. 所以 r= π2 1 k . 又根据实际情况可知 r 是圆的半径，故 r>0. 所以应有 k>0 且 k∈Z，即 k∈N*. 所以所求摆线的参数方程是        )cos1(π2 1 )sin(π2 1 φky= ,φφkx= (φ为参数)(其中 k∈N*). 点评:本题易错点是误把点(1，0)中的 1 或 0 当成φ的值，代入参数方程中求出 x 和 y 的值， 再计算 r 的值；或者在求出 cosφ=1 后，直接得出φ=0，从而导致答案不全面. 【例 4】已知圆的直径为 2，其渐开线的标准参数方程对应的曲线上两点 A、B 对应的参数分 别是 3 π 和 2 π ，求 A、B 两点的距离. 解析:首先根据圆的直径可知半径为 1，写出渐开线的标准参数方程，再根据 A、B 对应的参 数代入参数方程可得对应的 A、B 两点的坐标，然后使用两点之间的距离计算公式可得 A、B 之间的距离. 解:根据条件可知圆的半径是 1， 所以对应的渐开线参数方程是      φφφy= φ,φφx= cossin sincos (φ为参数)，分别把φ= 3 π 和φ= 2 π 代入， 可得 A、B 两点的坐标分别为 A( 6 π33,6 π33  )、B( 2 π ,1). 那么，根据两点之间的距离公式可得 A、B 两点的距离为 |AB|= 22 )16 π33()2 π 6 π33(  = ,63336-π6π)3613(6 1 2  即点 A、B 之间的距离为 .63336-π6π)3613(6 1 2  点评:本节主要内容是圆的渐开线和摆线的定义和参数方程.要解决有关的问题首先要理解 这两个定义和参数方程的推导过程，还要牢记两个参数方程.给出圆的半径要能写出对应的 参数方程，根据参数方程能写出某对应参数的坐标，从而再解决其他问题.本例题就是对这 些知识的综合考查，要注意前后知识的联系.特别是两点之间的距离公式也要熟记. 【例 5】已知圆 C 的参数方程是    6sinα+-2= 6cosα+1= y x ， (α为参数)和直线 l 对应的普通方程是 x-y-6 2 =0. (1)如果把圆心平移到原点 O，请问平移后圆和直线满足什么关系? (2)写出平移后圆的摆线方程. (3)求摆线和 x 轴的交点. 解析:(1)圆 C 平移后圆心为 O(0,0),它到直线 x-y-6 2 =0 的距离为 d= 2 26 =6, 恰好等于圆的半径,所以直线和圆是相切的. (2)由于圆的半径是 6,所以可得摆线方程是    φ-y= φ,φ-x= cos66 sin66 (φ为参数). (3)令 y=0,得 6-6cosφ=0 cosφ=1.所以φ=2kπ(k∈Z). 代入 x 得 x=2kπ(k∈Z), 即圆的摆线和 x 轴的交点为(2kπ,0)(k∈Z).