人教A版数学必修一2-1-2指数函数及其性质（1） 5页

2.1.2 指数函数及其性质（2 个课时） 一. 教学目标： 1．知识与技能 ①通过实际问题了解指数函数的实际背景； ②理解指数函数的概念和意义，根据图象理解和掌握指数函数的性质. ③体会具体到一般数学讨论方式及数形结合的思想； 2．情感、态度、价值观 ①让学生了解数学来自生活，数学又服务于生活的哲理. ②培养学生观察问题，分析问题的能力. 3．过程与方法 展示函数图象，让学生通过观察，进而研究指数函数的性质. 二．重、难点 重点：指数函数的概念和性质及其应用. 难点：指数函数性质的归纳，概括及其应用. 三、学法与教具： ①学法：观察法、讲授法及讨论法. ②教具：多媒体. 第一课时 一．教学设想： 1. 情境设置 ①在本章的开头，问题（1）中时间 x 与 GDP 值中的 1.073 ( 20)xy x x   与问题(2) ]t5 1 301中时间t和C-14含量P的对应关系P=[( )2 ，请问这两个函数有什么共同特征. ②这两个函数有什么共同特征 1 57301] [( ) ]2 tP  t 57301把P=[( ) 变成2 ，从而得出这两个关系式中的底数是一个正数，自变量 为指数，即都可以用 xy a （ a ＞0 且 a ≠1 来表示）. 二．讲授新课 指数函数的定义 一般地，函数 xy a （ a ＞0 且 a ≠1）叫做指数函数，其中 x 是自变量，函数的定义 域为 R. 提问：在下列的关系式中，哪些不是指数函数，为什么？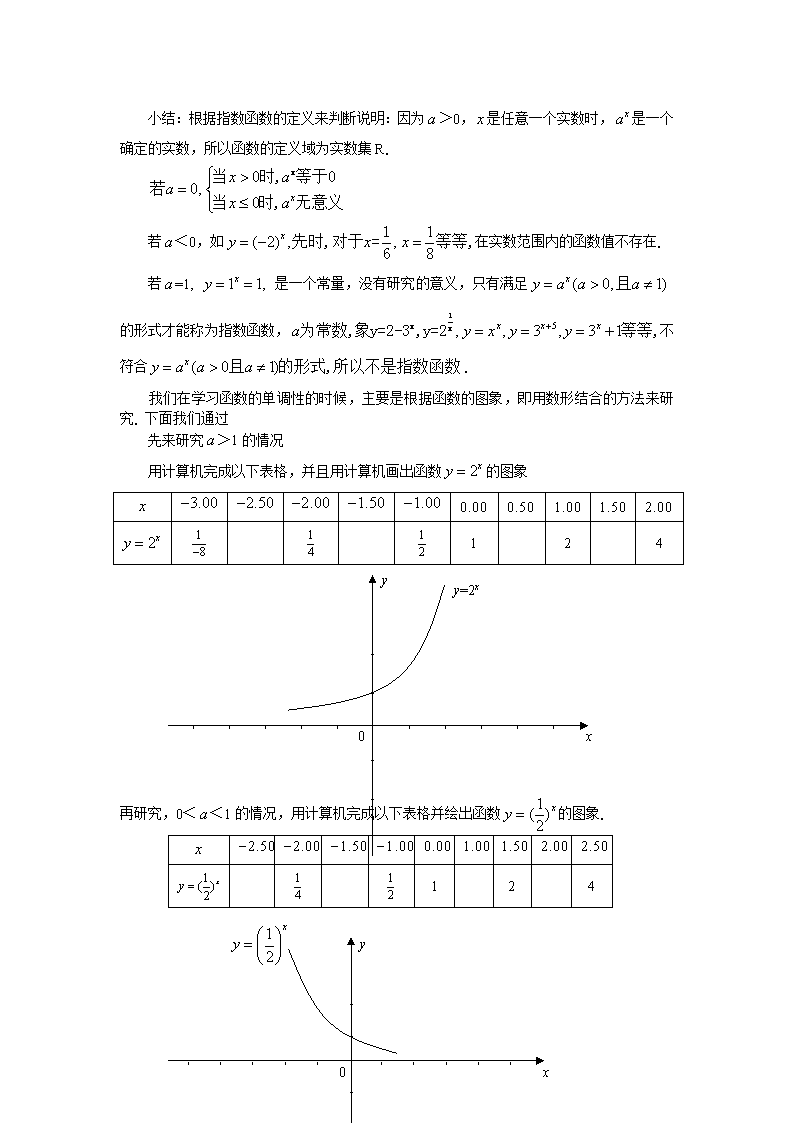 （1） 22xy  （2） ( 2)xy   （3） 2xy   （4） xy  （5） 2y x （6） 24y x （7） xy x （8） ( 1)xy a  （ a ＞1，且 2a  ） 小结：根据指数函数的定义来判断说明：因为 a ＞0， x 是任意一个实数时， xa 是一个 确定的实数，所以函数的定义域为实数集 R. 0 00, 0 x x aa x a     x当 时, 等于若 当 时, 无意义 若 a ＜0，如 1( 2) , , 8 xy x x  1先时,对于 = 等等,6 在实数范围内的函数值不存在. 若 a =1, 1 1,xy   是一个常量，没有研究的意义，只有满足 ( 0, 1)xy a a a  且 的 形式才能称为指数函数， 5, , 3 , 3 1x x xa y x y y    1 x x为常数,象y=2-3 ,y=2 等等,不符 合 ( 0 1)xy a a a  且 的形式,所以不是指数函数 . 我们在学习函数的单调性的时候，主要是根据函数的图象，即用数形结合的方法来研 究. 下面我们通过 先来研究 a ＞1 的情况 用计算机完成以下表格，并且用计算机画出函数 2xy  的图象 x 3.00 2.50 2.00 1.50 1.00 0.00 0.50 1.00 1.50 2.00 2xy  1 8 1 4 1 2 1 2 4 再研究，0＜ a ＜1 的情况，用计算机完成以下表格并绘出函数 1( )2 xy  的图象. x 2.50 2.00 1.50 1.00 0.00 1.00 1.50 2.00 2.50 1( )2 xy  1 4 1 2 1 2 4 - - - - - - ---- --- - x y 0 y=2x - - - - - ---- --- - x y 0 1 2 x y      - - - - - ---- --- - x y 0 从图中我们看出 12 ( )2 x xy y 与 的图象有什么关系? 通过图象看出 12 ( )2 x xy y y 与 的图象关于 轴对称, 实质是 2xy  上的 x,y点(- ) xy x,y y1与 =( ) 上点(- )关于 轴对称.2 讨论： 12 ( )2 x xy y 与 的图象关于 y 轴对称，所以这两个函数是偶函数，对吗？ ② 利 用 电 脑 软 件 画 出 1 15 , 3 , ( ) , ( )3 5 x x x xy y y y    的 函 数 图 象 . 8 6 4 2 -2 -4 -6 -8 -10 -5 5 10 问题：1：从画出的图象中，你能发现函数的图象与底数间有什么样的规律. 从 图 上 看 xy a （ a ＞ 1 ） 与 xy a （ 0 ＜ a ＜ 1 ） 两 函 数 图 象 的 特 征 . 8 6 4 2 -2 -4 -6 -8 -10 -5 5 10 问题 2：根据函数的图象研究函数的定义域、值域、特殊点、单调性、最大（小）值、 奇偶性. 问题 3：指数函数 xy a （ a ＞0 且 a ≠1），当底数越大时，函数图象间有什么样的关系. 图象特征 函数性质 a ＞1 0＜ a ＜1 a ＞1 0＜ a ＜1 向 x 轴正负方向无限延伸 函数的定义域为 R 图象关于原点和 y 轴不对称 非奇非偶函数 3xy  5xy  1 3 x y      1 5 x y      0 ( 1)xy a a (0 1)xy a a   0 函数图象都在 x 轴上方 函数的值域为 R+ 函数图象都过定点（0，1） 0a =1 自左向右， 图象逐渐上升 自左向右， 图象逐渐下降 增函数 减函数 在第一象限内的图 象纵坐标都大于 1 在第一象限内的图 象纵坐标都小于 1 x ＞0， xa ＞1 x ＞0， xa ＜1 在第二象限内的图 象纵坐标都小于 1 在第二象限内的图 象纵坐标都大于 1 x ＜0， xa ＜1 x ＜0， xa ＞1 5．利用函数的单调性，结合图象还可以看出： （1）在[ , ] xa b f x a上, ( )= （ a ＞0 且 a ≠1）值域是[ ( ), ( )] [ ( ), ( )];f a f b f b f a或 （2）若 0,x f x f x x  则 ( ) 1; ( )取遍所有正数当且仅当 R; （3）对于指数函数 ( ) xf x a （ a ＞0 且 a ≠1），总有 (1) ;f a （4）当 a ＞1 时，若 1x ＜ 2x ，则 1( )f x ＜ 2( )f x ； 例题： 例 1：（P56 例 6）已知指数函数 ( ) xf x a （ a ＞0 且 a ≠1）的图象过点（3，π），求 (0), (1), ( 3)f f f  的值. 分析：要求 (0), (1), ( 3) , ,xf f f a x  1 3的值,只需求出 得出f( )=( ) 再把 0，1，3 分别 代入 x ，即可求得 (0), (1), ( 3)f f f  . 提问：要求出指数函数，需要几个条件？ 课堂练习：P58 练习：第 1，2，3 题 补充练习：1、函数 1( ) ( )2 xf x  的定义域和值域分别是多少? 2、当 [ 1,1] , ( ) 3 2xx f x   时 函数 的值域是多少? 解（1） , 0x R y  （2）（－ 5 3 ，１） 例 2：求下列函数的定义域： （1） 4 42 xy  （2） | |2( )3 xy  分析：类为 ( 1, 0)xy a a a   的定义域是 R，所以，要使（1），（2）题的定义域，保 要使其指数部分有意义就得 . 3．归纳小结 作业：P59 习题 2.1 A 组第 5、6 题 1、理解指数函数 ( 0), 1 0 1xy a a a a    注意 与 两种情况。 2、解题利用指数函数的图象，可有利于清晰地分析题目，培养数型结合与分类讨论的 数学思想 .