山东省淄博市2020-2021学年高一上学期期末数学试题 12页

参照秘密级管理★启用前 普通高中高一期未质量检测 数学 注意事项： 1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上． 2．回答选择题时，选出每个小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需 改动，用橡皮擦干净后，再选涂其它答案标号．回答非选择题时，将答案写在答题卡上．写 在本试卷上无效． 3．考试结束后，将本试卷和答题卡一并交回． 一、单项选择题：本题共 8 小题，每小题 5 分，共 40 分．在每小题给出的四个选项中，只有 一项是符合题目要求的． 1．已知集合 13 , { 3, 2, 1,0,1,2}3 xA x B          ，则  RC A B  （ ） A．{ 3, 2}  B．{ 3, 2, 1}   C．{0,1,2} D．{ 1,0,1,2} 2．已知扇形的周长为 8，扇形圆心角的弧度数是 2，则扇形的面积为（ ） A．2 B．4 C．6 D．8 3．下列函数是偶函数且在 (0, ) 上单调递增的是（ ） A． 1 2( )f x x  B． ( ) 3 xf x  C． 2( ) log | |f x x D． 4 1( )f x x  4．用二分法求方程 2log 2x x  的近似解时，可以取的一个区间是（ ） A． (0,1) B． (1,2) C． (2,3) D． (3,4) 5．已知 11 32 52 , 3 , ln 2a b c   ，则（ ） A．b c a  B． a c b  C．b a c  D． a b c  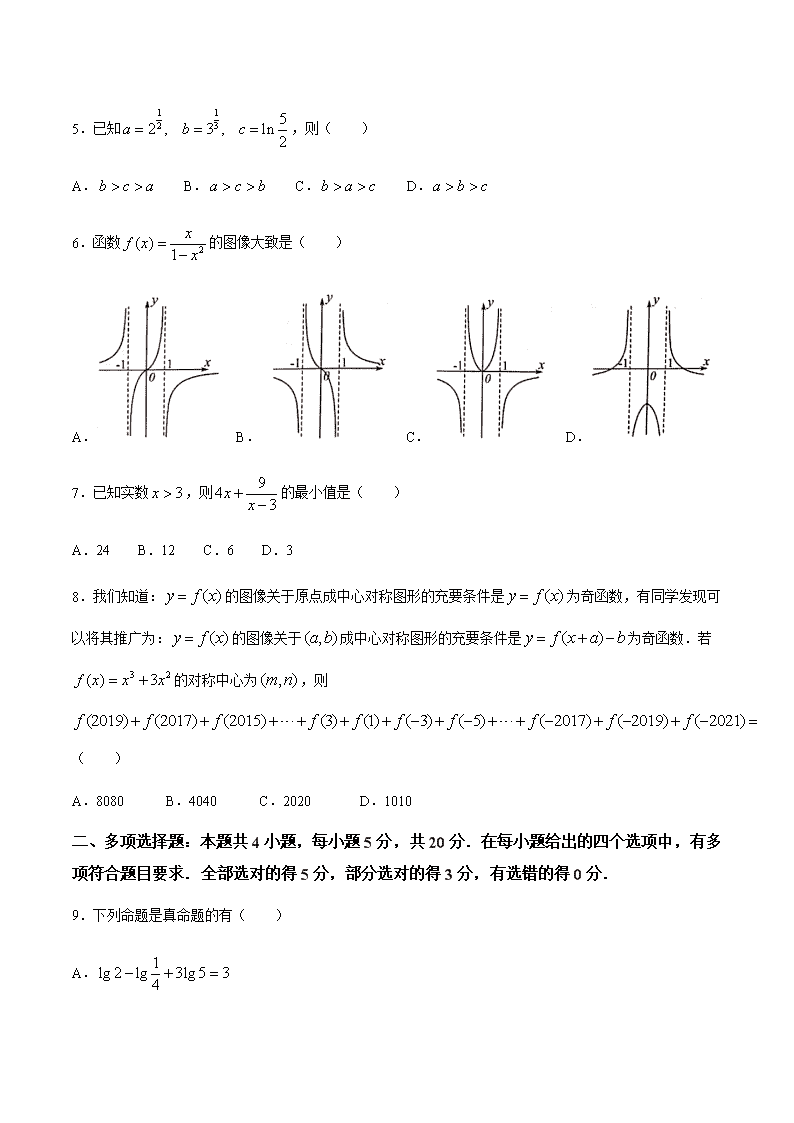6．函数 2( ) 1 xf x x   的图像大致是（ ） A． B． C． D． 7．已知实数 3x  ，则 94 3x x   的最小值是（ ） A．24 B．12 C．6 D．3 8．我们知道： ( )y f x 的图像关于原点成中心对称图形的充要条件是 ( )y f x 为奇函数，有同学发现可 以将其推广为： ( )y f x 的图像关于 ( , )a b 成中心对称图形的充要条件是 ( )y f x a b   为奇函数．若 3 2( ) 3f x x x  的对称中心为 ( , )m n ，则 (2019) (2017) (2015) (3) (1) ( 3) ( 5) ( 2017) ( 2019) ( 2021)f f f f f f f f f f                  （ ） A．8080 B．4040 C．2020 D．1010 二、多项选择题：本题共 4 小题，每小题 5 分，共 20 分．在每小题给出的四个选项中，有多 项符合题目要求．全部选对的得 5 分，部分选对的得 3 分，有选错的得 0 分． 9．下列命题是真命题的有（ ） A． 1lg2 lg 3lg5 34    B．命题“ 0,2 1xx   ”的否定为“ 0,2 1xx   ” C．“  ”是“sin sin  ”成立的充分不必要条件 D．若幂函数 ( ) ( )f x x  R 经过点 1 ,28      ，则 3   10．若角 为钝角，且 1sin cos 5     ，则下列选项中正确的有（ ） A． 4sin 5   B． 4cos 5    C． 4tan 3    D． 12sin cos 25     11．设 0, 0a b c   ，则下列不等式成立的是（ ） A． a c b c   B． 2 2c c a b  C． a a c b b c   D． 1 1a ba b    12．三元均值不等式：“当 , ,a b c 均为正实数时， 3 3 a b c abc   ，即三个正数的算术平均数不小于它们 的几何平均数，当且仅当 a b c  时等号成立．”利用上面结论，判断下列不等式成立的有（ ） A．若 0x  ，则 2 2 3x x   B．若 0 1x  ，则 2 1(1 ) 9x x  C．若 0x  ，则 2 12 3x x   D．若 0 1x  ，则 2 1(1 ) 9x x  三、填空题：本题共 4 小题，每小题 5 分，共 20 分． 13．函数 211( ) 2 x f x      的值域为___________． 14．已知函数 2 2 3 , 0,( ) log , 0, x x xf x x x      若 ( ) 4f a  ，则实数 a  ___________； 15．若 1sin 3 5       ，则 2sin 3       ___________， 5cos 6       _________（第一空 2 分，第 二空 3 分）； 16．已知函数 2 2( ) 2 ( 0), ( ) 4 1xf x ax a g x x x      ．若对任意 1 [ 1,2]x   ，总存在 2 [ 1,2]x   ，使 得    1 2f x g x ，则实数 a 的取值范围是__________． 四、解答题：本题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤． 17．（10 分）已知角 终边上一点 (1,2)P ． （1）求 sin 2cos sin cos       的值； （2）求 11 9cos sin2 2               的值． 18．（12 分）已知集合  2{ ( )( 1) 0}( ), 1 log 1A x x a x a B x x        R∣ ∣ ． （1）当 1a  时，求 A B ； （2）是否存在实数 a ，使得________成立？ 请在① A B B  ，② A B   ，③  RB A ð 这三个条件中任选一个，补充在上面的问题中；若问题 中的实数 a 存在，求出 a 的取值范围；若不存在，说明理由． 19．（12 分）已知函数 ( ) sin 2 ( 0, )6g x a x b a b        R ．若函数 ( )g x 在区间 0, 2      上的最大值为 3，最小值为 0． （1）求函数 ( )g x 的解析式； （2）求出 ( )g x 在 (0, ) 上的单调递增区间． 20．（12 分）某乡镇为打造成“生态农业特色乡镇”，决定种植某种水果，该水果单株产量 ( )M x （单位：千 克）与施用肥料 x （单位：千克）满足如下关系：  25 3 , 0 2 ( ) 50 5 , 2 51 3 x x M x x xx          ，单株成本投入（含施肥、人工等）为 30x 元．已知这种水果的市场售价 为 15 元/千克，且销路畅通供不应求，记该水果树的单株利润为 ( )f x （单位：元）． （1）求 ( )f x 的函数关系式； （2）当施用肥料为多少千克时，该水果树的单株利润最大？最大利润是多少？ 21．（12 分）已知一元二次函数 2( ) 1 ( 0)f x ax x a    ． （1）若 0 1a  ，证明函数 ( )f x 在区间 1, 2     上单调递减； （2）若函数 ( )f x 在区间[1,4] 上的最小值为 2 ，求实数 a 的值． 22．（12 分）函数 ( )f x 的定义域为 D ，若 0x D ，满足  0 0f x x ，则称 0x 为 ( )f x 的不动点． 已知函数 3 3 3 , 0 1( ) , ( ) ( ( ))log ,1 3 x xf x g x f f xx x       ． （1）试判断 ( )g x 不动点的个数，并给予证明； （2）若“ 3 3 20, , ( ) 1 log (1 ) log ( )3x g x x x k         ”是真命题，求实数 k 的取值范围． 普通高中高一期未质量检测数学参考答案 一、单项选择题 1．D；2．B；3．C；4．B；5．C；6．A；7．A；8．B； 二、多项选择题： 9．AC；10．BD；11．AD；12．AC； 三、填空题：本题共 4 小题，每小题 5 分，共 20 分． 13． 1 ,2    ；14． 1 或 16；15． 1 1,5 5  ；16． 10, 2      ． 四、解答题：本题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤． 17．解：（1）因为 终边上一点 (1,2)P ，所以 tan 2y x    ， 2 分 且 sin 2cos tan 2 4sin cos tan 1           ． 5 分 （2）已知角 终边上一点 (1,2)P ，则 2 2| | 1 2 5r OP    ， 6 分 所以 2 2sin 555 y r     ， 7 分 1 5cos 55 x r     ， 8 分 11 9 5cos sin sin cos2 2 5                      ． 10 分 18．解：（1）若 1a  ，则 { ( 1)( 1) 0} ( , 1) (1, )A x x x        ∣ ， 解不等式 21 log 1x   ，得 1 12, ,22 2x B        ， 所以 (1,2]A B  ； 4 分 （2）显然 1 ,22B      ，若选① A B B  ，则 B A ，当 1a   时，集合 ( , 1) ( , )A a     ， 要使 B A ，则需 1 2a  ，所以 11 2a   ； 7 分 当 1a   时，集合 ( , ) ( 1, )A a     ，此时 B A 10 分 所以若选①，则实数 a 的取值范围为 1 2a  ； 12 分 若选② A B  ，当 1a   时，集合 ( , 1) ( , )A a     ， 要使 A B   ，则需 2a  ，所以 2a  ； 7 分 当 1a   时，集合 ( , ) ( 1, )A a     ，此时 ,B A A B B     10 分 所以若选②，则实数 a 的取值范围为 2a  ； 12 分 若选③  R 1, ,22B A B      ð ，当 1a   时，集合 R( , 1) ( , ), [ 1, ]A a C A a       ， 要使  B A Rð ，则需 2a  ，所以 2a  ； 6 分 当 1a   时，集合 ( , 1) ( 1, )A       ，此时  { 1}RC A   ，不满足题意； 8 分 当 1a   时，集合 ( , ) ( 1, )A a     ，此时  R R[ , 1],C A a B A    ð 10 分 所以若选③，则实数 a 的取值范围为 2a  ； 12 分 19．解：（1）由题意知，若 0, 2x     ，则 726 6 6x     ， 所以 1sin 2 ,16 2x             ， 2 分 又因为 0a  ，所以 3 1 02 a b a b     ，得 2 1 a b    ； 4 分 所以 ( ) 2sin 2 16g x x       ； 6 分 （2）因为 (0, )x  ，所以 1326 6 6x     ， 8 分 正弦函数 siny x 在区间 13,6 6       上的单调递增区间为 ,6 2       和 3 13,2 6      ， 10 分 此时即 26 6 2x     或 3 1322 6 6x     ， 得 0 6x   或 2 3 x   ，所以 ( )g x 在 (0, ) 上的递增区间为 0, 6      和 2 ,3      12 分 另解：当 2 2 2 ,2 6 2k x k k        Z ，得到 ,3 6k x k k      Z 7 分 当 0k  时， 3 6x    ； 8 分 当 1k  时， 2 7 3 6x   ， 9 分 所以 ( )g x 在 (0, ) 上的递增区间为 0, 6      和 2 ,3      12 分 20．解：（1）由题意得： ( ) 15 ( ) 30f x M x x  ，  2 215 5 3 30 ,0 2 75 30 225,0 2 ( ) 75050 30 25, 2 515 30 25, 2 5 11 x x x x x x f x xx x xx x xx                         （每段解析式正确 2 分） 4 分 （2）由（1）中 275 30 225,0 2, ( ) 750 30 25, 2 5.1 x x x f x x x xx            得 2175 222,0 2,5( ) 25805 30 (1 ) , 2 5.1 x x f x x xx                      6 分 （i）当 0 2x  时， max( ) (2) 465f x f  ； 8 分 （ii）当 2 5x  时， 25 25( ) 805 30 (1 ) 805 30 2 (1 ) 5051 1f x x xx x               11 分 当且仅当 25 11 xx   时，即 4x  时等号成立． 因为 465 505 ，所以当 4x  时， max( ) 505f x  ， 所以当施用肥料为 4 千克时，种植该果树获得的最大利润是 505 元 12 分 21．解：（1）设 1 2 1 2x x  ， 则            2 2 1 2 1 1 2 2 1 2 1 21 1 1f x f x ax x ax x x x a x x             ， 3 分 因为 1 2x x ，得 1 2 0x x  ；因为 1 2 1 1,2 2x x  ，得 1 2 1x x  ， 且 0 1a  ，得  1 2 1a x x a   ，即  1 2 1 0a x x   ； 所以    1 2 0f x f x  成立，即    1 2f x f x ； 函数 ( )f x 在区间 1, 2     上单调递减； 6 分 （2）当 0a  时，二次函数的对称轴为 1 2x a  ，且 1 02a  ， 函数 2( ) 1f x ax x   在区间[1,4] 上单调递减， 此时 min( ) (4) 16 3 2f x f a     ，得 1 16a  ，不符合题意； 7 分 当 10 8a  时，二次函数的对称轴为 1 2x a  ，且 1 42a  ， 函数 2( ) 1f x ax x   在区间[1,4] 上单调递减， 此时 min( ) (4) 16 3 2f x f a     ，得 1 16a  ，符合题意； 8 分 当 1 1 8 2a  时，二次函数的对称轴为 1 2x a  ，且 11 42a   ， 函数 2( ) 1f x ax x   的最小值为 min 4 1( ) 24 af x a    ， 得 1 12a  ，不符合题意； 9 分 当 1 2a  时，二次函数的对称轴为 1 2x a  ，且 10 12a   ， 函数在区间[1,4] 上单调递增， min( ) (1) 2f x f a    ，不符合题意； 10 分 所以当函数 ( )f x 在区间[1,4] 上的最小值为 2 时，实数 1 16a  ． 12 分 另解：若函数 ( )f x 在区间[1,4] 上的最小值为 2 ， 即不等式 2 1 2ax x    在区间[1,4] 上恰好成立（能取到等号）， 等价于不等式 21 13a x x       在区间[1,4] 上恰好成立， 8 分 构造函数 2 1 1( ) 3 ,14g t t t t x            不等式成立只需要 a 等于函数 2( ) 3g t t t   在区间 1 ,14      上的最大值； 显然函数 2( ) 3g t t t   在区间 1 ,14      上的最大值为 1 1 4 16g      ， 10 分 所以实数 1 16a  ． 12 分 22．解：（1） ( ) ( ( ))g x f f x ， 若 20 3x  ，则1 3 3 3x   ，所以 3( ) log (3 3 )g x x  ， 3 3( ) log (3 3 ) 1 log (1 )g x x x x x x        ， 因为函数 3( ) log (1 ) 1h x x x    在 20, 3     是单调递增的， 3 3 3 1 1 1 1 2 3(0) 1 0, log 1 1 log 2 1 log 02 2 2 2 3h h                      ， 所以 ( )h x 在 20, 3     内存在唯一零点； 2 分 若 2 13 x  ，则 0 3 3 1x   ，所以 ( ) 3 3(3 3 ) 9 6g x x x     ， ( ) 9 6g x x x x    ，解得 3 4x  ； 3 分 若1 3x  ，则 30 log 1x  ，所以 3( ) 3 3logg x x  ， 3( ) 3 3logg x x x x    ； 3( ) 3log 3x x x    在 (1,3] 是单调递增的， 3 3 4 4 5 14(3) 3 0, 3log log 64 03 3 3 3             ， 所以 3( ) 3log 3x x x    在 (1,3] 内有唯一零点； 5 分 综上所述， ( )g x 有 3 个不动点． 6 分 （2）由（1）可知，当 3 20, , ( ) ( ( )) log (3 3 )3x g x f f x x      ， 若“ 3 3 20, , ( ) 1 log (1 ) log ( )3x g x x x k         ”是真命题 就是 20, 3x      ，使不等式 3 3( ) 1 log (1 ) log ( )g x x x k     成立 等价于 3 3 2 10, , log log ( )3 1 xx k xx        成立， 即 20, 3x      ，不等式组 1 1 0 x k xx x k        成立， 2(1 ) (1 ) 2 0 0 x k x x k          ， 解得 2 28 81 12 2 k k k kx x k                ， 8 分 因为 20, 3x     ，保证 0x k  ，所以 2 3k   因为 2 28 2 81 02 2 k k k kk                ， 2 28 2 81 ( ) 02 2 k k k kk           ， 所以 2 81 2 k kk x        10 分 所以 2 81 02 2 3 k k k         ，解得： 2 13 k   ． 所以实数 k 的取值范围是 2 ,13     12 分 解法 2：由（1）可知，当 3 20, , ( ) ( ( )) log (3 3 )3x g x f f x x      ， 若“ 3 3 20, , ( ) 1 log (1 ) log ( )3x g x x x k         ”是真命题 就是 20, 3x      ，使不等式 3 3( ) 1 log (1 ) log ( )g x x x k     成立 等价于 3 3 2 10, , log log ( )3 1 xx k xx        成立， 等价于 20, 3x      ，使 1 1 x k xx    成立， 且 0x k  也成立 8 分 1 2 (1 )1 1 x k x x kx x         ，设 2 (1 )1y xx    ， 20, 3x      ，使 1 1 x k xx    成立 只要 maxy k 即可，函数 2 (1 )1y xx    在 20, 3     上单调递减， 所以 max 1y  ，所以1 k ， 10 分 20, 3x      ，使 0x k  在区间 20, 3     成立，只需要 max( ) 0x k  即可，即 2 203 3k k     所以实数 k 的取值范围是 2 ,13     12 分 解法 3：由（1）可知，当 3 20, , ( ) ( ( )) log (3 3 )3x g x f f x x      若“ 3 3 20, , ( ) 1 log (1 ) log ( )3x g x x x k         ”是真命题 就是 20, 3x      ，使不等式 3 3( ) 1 log (1 ) log ( )g x x x k     成立 等价于 3 3 2 10, , log log ( )3 1 xx k xx        成立， 它的否定是： 3 3 2 10, ,log log ( )3 1 xx k xx        恒成立， 或 20, , 03x x k      ，（原不等式不存在．．．．．．．）注意：命题否定的意义 即 3 3 1log log ( )1 x k xx    在 20, 3     上恒成立，或者 0x k  在 20, 3     上恒成立， 8 分 若 3 3 1log log ( )1 x k xx    在 20, 3     上恒成立 则 2 (1 )1 0 x kx x k         在 20, 3     上恒成立，设 2 (1 )1y xx    ， 只需要 maxy k 且 min( ) 0x k  即可，所以 1k  ， 10 分 若 0x k  在 20, 3     上恒成立，则 2 3k   ， 所以， 1k  或 2 3k   ， 11 分 所以当 2 13 k   时，所以 20, 3x      ，使不等式 3 3( ) 1 log (1 ) log ( )g x x x k     成立 实数 k 的取值范围是 2 ,13     12 分