高中数学必修1教案：第九章直线平面简单几何体(B)(第28课)棱柱和棱锥(4) 6页

课 题：9．9棱柱和棱锥(四) ‎ 教学目的：‎ ‎1. 掌握直棱柱和正棱锥的直观图的画法；‎ ‎2．培养画图、视图、析图的能力；‎ ‎3．了解正多面体的概念，了解正多面体只有5种 ‎4. 进一步理解和掌握棱柱的性质及有关概念.‎ ‎5.掌握棱柱的有关面积、体积的计算.‎ 教学重点：坐标系的建立、顶点的确定 教学难点：坐标系的建立、顶点的确定 授课类型：新授课 ‎ 课时安排：1课时 ‎ 教 具：多媒体、实物投影仪 ‎ 教学过程：‎ 一、复习引入：‎ ‎1 多面体的概念：由若干个多边形围成的空间图形叫多面体；每个多边形叫多面体的面，两个面的公共边叫多面体的棱，棱和棱的公共点叫多面体的顶点，连结不在同一面上的两个顶点的线段叫多面体的对角线．‎ ‎2．凸多面体：把多面体的任一个面展成平面，如果其余的面都位于这个平面的同一侧，这样的多面体叫凸多面体．如图的多面体则不是凸多面体．‎ ‎3．凸多面体的分类：多面体至少有四个面，按照它的面数分别叫四面体、五面体、六面体等 ‎4．棱柱的概念：有两个面互相平行，其余每相邻两个面的交线互相平行，这样的多面体叫棱柱两个互相平行的面叫棱柱的底面（简称底）；其余各面叫棱柱的侧面；两侧面的公共边叫棱柱的侧棱；‎ 两底面所在平面的公垂线段叫棱柱的高（公垂线段长也简称高）‎ ‎5．棱柱的分类：侧棱不垂直于底面的棱柱叫斜棱柱侧棱垂直于底面的棱柱叫直棱柱 底面的是正多边形的直棱柱叫正棱柱棱柱的底面可以是三角形、四边形、五边形……这样的棱柱分别叫三棱柱、四棱柱、五棱柱……‎ ‎6．棱柱的性质 ‎（1）棱柱的侧棱相等，侧面都是平行四边形；直棱柱侧面都是矩形；正棱柱侧面都是全等的矩形；‎ ‎（2）棱柱的两个底面与平行于底面的截面是对应边互相平行的全等的多边形（图（1））；‎ ‎（3）过棱柱不相邻的两条侧棱的截面都是平行四边形（图（2））‎ ‎7 平行六面体、长方体、正方体：底面是平行四边形的四棱柱是平行六面体．侧棱与底面垂直的平行六面体叫直平行六面体，底面是矩形的直平行六面体长方体，棱长都相等的长方体叫正方体．‎ ‎8．平行六面体、长方体的性质 ‎(1)平行六面体的对角线交于一点，求证：对角线相交于一点，且在点处互相平分．‎ ‎(2)长方体的一条对角线长的平方等于一个顶点上的三条棱长的平方和 ‎9 棱锥的概念：有一个面是多边形，其余各面是有一个公共顶点的三角形，这样的多面体叫棱锥其中有公共顶点的三角形叫棱锥的侧面；多边形叫棱锥的底面或底；各侧面的公共顶点，叫棱锥的顶点，顶点到底面所在平面的垂线段，叫棱锥的高（垂线段的长也简称高）．‎ ‎10．棱锥的表示：棱锥用顶点和底面各顶点的字母，或用顶点和底面一条对角线端点的字母来表示 如图棱锥可表示为，或．‎ ‎11．棱锥的分类：（按底面多边形的边数）‎ 分别称底面是三角形，四边形，五边形……的棱锥为三棱锥，四棱锥，五棱锥……（如图）‎ ‎12．棱锥的性质：‎ 定理：如果棱锥被平行于底面的平面所截，那么所得的截面与底面相似，截面面积与底面面积比等于顶点到截面的距离与棱锥高的平方比．‎ 中截面：经过棱锥高的中点且平行于底面的截面，叫棱锥的中截面 ‎13．正棱锥：底面是正多边形，顶点在底面上的射影是底面的中心的棱锥叫正棱锥．‎ ‎（1）正棱锥的各侧棱相等，各侧面是全等的等腰三角形，各等腰三角形底边上的高相等（叫正棱锥的斜高）．‎ ‎（2）正棱锥的高、斜高、斜高在底面上的射影组成一个直角三角形；正棱锥的高、侧棱、侧棱在底面上的射影也组成一个直角三角形 ‎14．斜二测画法的规则 二、讲解新课：‎ ‎1 直棱柱、正棱锥的直观图的画法：（见下面的例1，例2）‎ ‎2．正多面体 正方体是一类非常特别的多面体：它的六个面都是正方形，每个顶点处都有三条棱． 正三棱锥，它的四个面都是三角形，每个顶点处都有三条棱．正三棱锥有四个面，我们也把它称为正四面体．正方体我们也可以称为正六面体． ‎ 每个面都是有相同边数的正多边形，每个顶点为端点都有相同棱数的凸多面体，叫做正多面体．‎ ‎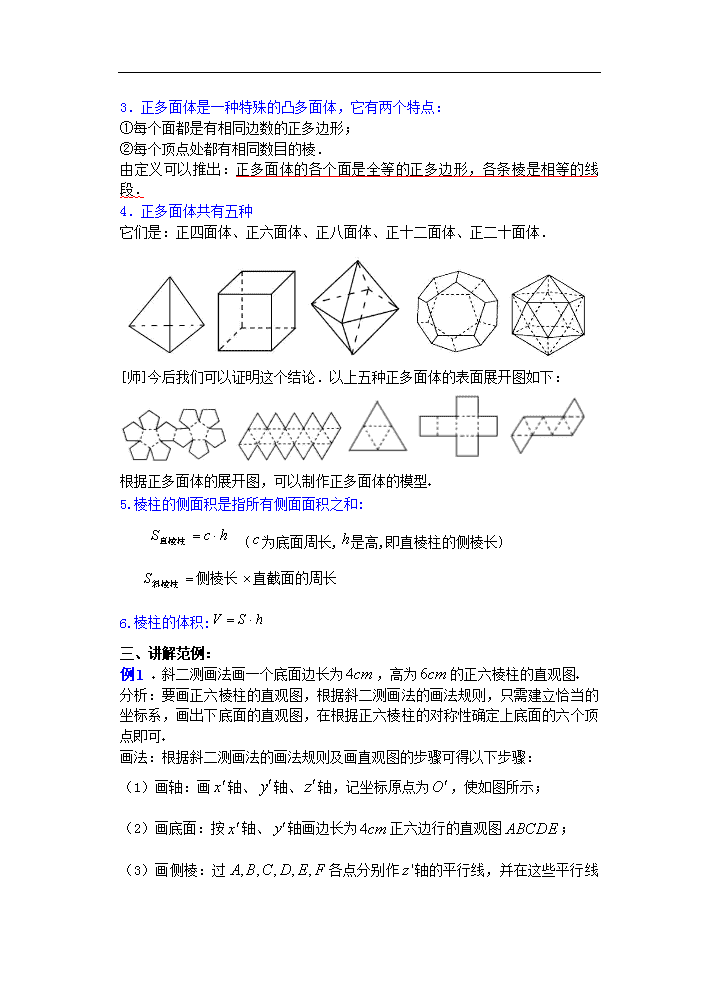3．正多面体是一种特殊的凸多面体，它有两个特点：‎ ‎①每个面都是有相同边数的正多边形；‎ ‎②每个顶点处都有相同数目的棱．‎ 由定义可以推出：正多面体的各个面是全等的正多边形，各条棱是相等的线段．‎ ‎4．正多面体共有五种 它们是：正四面体、正六面体、正八面体、正十二面体、正二十面体．‎ ‎ ‎ ‎[师]今后我们可以证明这个结论．以上五种正多面体的表面展开图如下：‎ 根据正多面体的展开图，可以制作正多面体的模型 ‎5.棱柱的侧面积是指所有侧面面积之和:‎ ‎ (为底面周长,是高,即直棱柱的侧棱长)‎ ‎6.棱柱的体积:‎ 三、讲解范例：‎ 例1 斜二测画法画一个底面边长为，高为的正六棱柱的直观图 分析：要画正六棱柱的直观图，根据斜二测画法的画法规则，只需建立恰当的坐标系，画出下底面的直观图，在根据正六棱柱的对称性确定上底面的六个顶点即可 画法：根据斜二测画法的画法规则及画直观图的步骤可得以下步骤：‎ ‎（1）画轴：画轴、轴、轴，记坐标原点为，使如图所示；‎ ‎（2）画底面：按轴、轴画边长为正六边行的直观图；‎ ‎（3）画侧棱：过各点分别作 轴的平行线，并在这些平行线上截取、、、、、，使它们都等于；‎ B C D F E A B C D F E A ‎（4）成图：顺次连结,并加以整理(去掉辅助线,并将被遮住的部分该为虚线),就得到正六棱柱的直观图 ‎ ‎ 说明： 本题的关键是建立恰当的三维坐标系及画正六边行的直观图,我们选择恰当的坐标系的标准是尽可能的使所画平面图形的边和坐标轴平行或在坐标轴上 例2．画一个底面边长为,高为的正五棱锥的直观图,比例尺为.‎ 分析：画正五棱锥的直观图只需根据斜二侧画法,选择恰当的坐标系画出正五边形的直观图,进而确定出正五棱锥的顶点即可.‎ 画法：（1）画轴：画轴、轴、轴，记坐标原点为，使（或），使；‎ ‎（2）画底面：轴、轴画边长为正五边形的直观图并使正五边行的中心对应与点；‎ ‎（3）画高线：在轴上取；‎ ‎（4）成图：顺次连结,并加以整理(去掉辅助线,并将被遮住的部分该为虚线),就得到正棱锥的直观图 ‎ ‎ 说明：正棱锥的直观图由底面和顶点所决定正棱锥底面的画法与直棱柱底面的画法相同顶点和底面中心的距离等于它的高画正棱锥的直观图可以对照直棱柱的直观图的画法,加深对空间图形直观图画法的理解和掌握.‎ C B O C1‎ B1‎ A1‎ A 例3 斜三棱柱的底面的边长是‎4cm的正三角形,侧棱长为‎3cm,侧棱与底面相邻两边都成角.‎ ‎(1)求证:侧面是矩形;‎ ‎(2)求这个棱柱的侧面积;‎ ‎(3)求棱柱的体积.‎ 证明(1):∵与所成的角都为,‎ ‎∴A在面ABC上的射影O在的平分线上.‎ 又∵是正三角形 ‎∴ ∴.‎ 又∵, ∴,‎ ‎∴四边形是矩形.‎ ‎(2)解:,‎ ‎∴‎ 又,‎ ‎∴.‎ ‎ (3)解:作,垂足为E,连结AE,则.‎ ‎ 在中, ‎ ‎ 在中, ‎ ‎ 在中, ‎ ‎ ∴‎ 四、课堂练习：‎ ‎1下列各图中，哪些是正方体的表面展开图？哪些不是？‎ 五、小结 ：‎ ‎⒈直棱柱和正棱锥的直观图的画法，为今后在多面体中解题奠定了基础．在画图时底面要画成水平放置的平面图形的直观图，要注意直棱柱的侧棱和正棱锥的顶点的确定方法．‎ ‎⒉对于正多面体要准确理解概念，理解正多面体的各面是全等的正多边形，各侧棱是相等的线段；了解正多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体五种 ‎ 六、课后作业：‎ 七、板书设计（略）‎ 八、课后记：‎