高中数学必修3教案：1_3_1进位制 2页

‎1.3.1‎进位制 教学要求：了解各种进位制与十进制之间转换的规律，会利用各种进位制与十进制之间的联系进行各种进位制之间的转换；学习各种进位制转换成十进制的计算方法，研究十进制转换为各种进位制的除k去余法，并理解其中的数学规律. 教学重点：各种进位制之间的互化. 教学难点：除k取余法的理解以及各进位制之间转换的程序框图及其程序的设计. 教学过程： 知识探究(一):进位制的概念 思考1:进位制是为了计数和运算方便而约定的记数系统，如逢十进一，就是十进制；每七天为一周，就是七进制；每十二个月为一年，就是十二进制，每六十秒为一分钟，每六十分钟为一个小时，就是六十进制；等等.一般地，“满k进一”就是k进制，其中k称为k进制的基数.那么k是一个什么范围内的数？ 思考2:十进制使用0～9十个数字，那么二进制、五进制、七进制分别使用哪些数字？ 思考3:在十进制中10表示十，在二进制中 ‎10表示2.一般地，若k是一个大于1的整数，则以k为基数的k进制数可以表示为一串数 字连写在一起的形式：anan-1…a‎1a0(k).其中各个数位上的数字an，an-1，…，a1，a0的取值范围如何？ 思考4:十进制数4528表示的数可以写成4×103+5×102+2×101+8×100，依此类 比，二进制数110011(2),八进制数7342(8)分别可以写成什么式子？ ‎110011(2)=1×25+1×24+0×23+0×22+1×21+1×20 ‎7342(8)=7×83+3×82+4×81+2×80. 思考5:一般地，如何将k进制数anan-1…a‎1a0(k)写成各数位上的数字与基数k的幂的乘积之和的形式？ 思考6:在二进制中，0+0，0+1，1+0，1+1的值分别是多少？ 知识探究(二):k进制化十进制的算法 思考1:二进制数110011(2)化为十进制数是什么数？ ‎110011(2)=1×25+1×24+0×23+0×22+1×21+1×20 =32+16+2+1=51. 思考2:二进制数右数第i位数字ai化为十进制数是什么数？‎ 例1 将下列各进制数化为十进制数.‎ ‎(1)10303(4) ； (2)1234(5).‎ ‎10303(4)=1×44+3×42+3×40=307.‎ ‎1234(5)=1×53+2×52+3×51+4×50=194. ‎ 知识探究(三):除k取余法 思考1:二进制数101101(2)化为十进制数是什么数？十进制数89化为二进制数是什么数？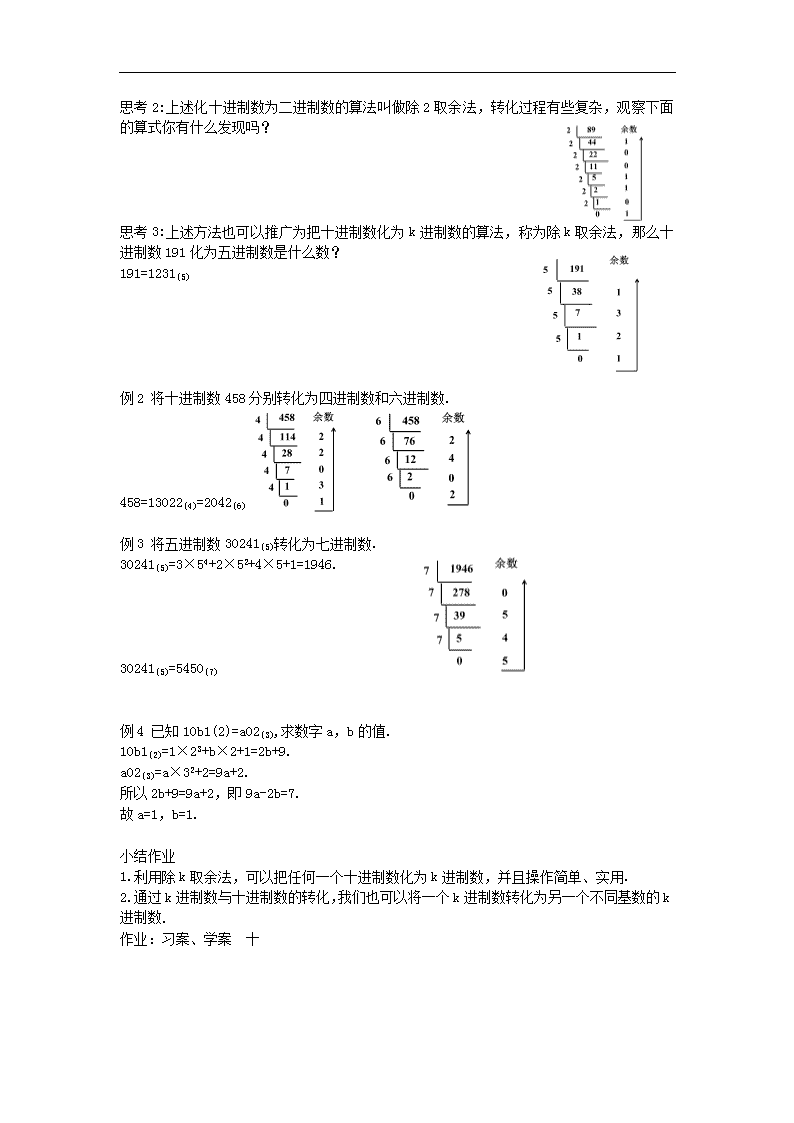‎ 思考2:上述化十进制数为二进制数的算法叫做除2取余法，转化过程有些复杂，观察下面的算式你有什么发现吗？ ‎ 思考3:上述方法也可以推广为把十进制数化为k进制数的算法，称为除k取余法，那么十进制数191化为五进制数是什么数？‎ ‎191=1231(5)‎ 例2 将十进制数458分别转化为四进制数和六进制数.‎ ‎458=13022(4)=2042(6)‎ 例3 将五进制数30241(5)转化为七进制数. ‎ ‎30241(5)=3×54+2×52+4×5+1=1946. ‎ ‎30241(5)=5450(7) ‎ 例4 已知10b1(2)=a02(3),求数字a，b的值.‎ ‎10b1(2)=1×23+b×2+1=2b+9.‎ a02(3)=a×32+2=‎9a+2.‎ 所以2b+9=9a+2，即9a-2b=7. ‎ 故a=1，b=1. ‎ 小结作业 ‎1.利用除k取余法，可以把任何一个十进制数化为k进制数，并且操作简单、实用.‎ ‎2.通过k进制数与十进制数的转化，我们也可以将一个k进制数转化为另一个不同基数的k进制数.‎ 作业：习案、学案 十