2020高中数学函数的表示法 4页

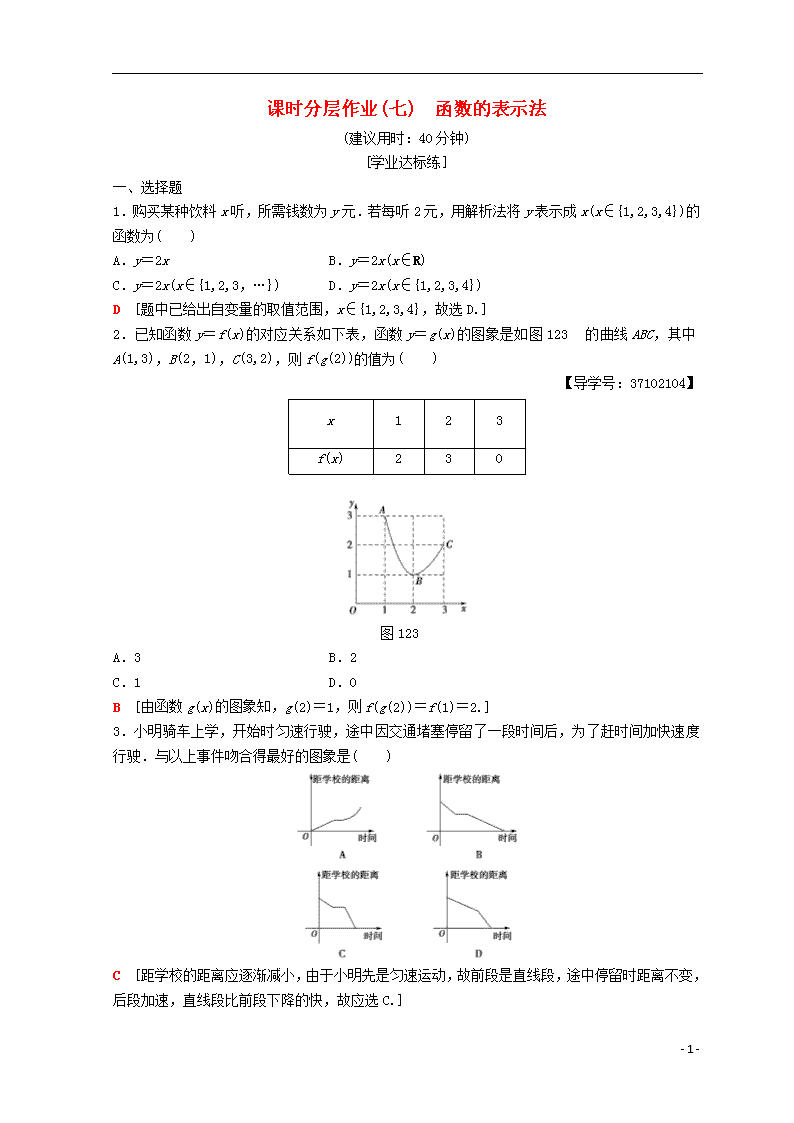
课时分层作业(七)　函数的表示法 ‎(建议用时：40分钟)‎ ‎[学业达标练]‎ 一、选择题 ‎1．购买某种饮料x听，所需钱数为y元．若每听2元，用解析法将y表示成x(x∈{1,2,3,4})的函数为(　　)‎ A．y＝2x　　　　　　　　 B．y＝2x(x∈R)‎ C．y＝2x(x∈{1,2,3，…}) D．y＝2x(x∈{1,2,3,4})‎ D　[题中已给出自变量的取值范围，x∈{1,2,3,4}，故选D.]‎ ‎2．已知函数y＝f(x)的对应关系如下表，函数y＝g(x)的图象是如图123的曲线ABC，其中A(1,3)，B(2，1)，C(3,2)，则f(g(2))的值为(　　) ‎ ‎【导学号：37102104】‎ x ‎1‎ ‎2‎ ‎3‎ f(x)‎ ‎2‎ ‎3‎ ‎0‎ 图123‎ A．3 B．2‎ C．1 D．0‎ B　[由函数g(x)的图象知，g(2)＝1，则f(g(2))＝f(1)＝2.]‎ ‎3．小明骑车上学，开始时匀速行驶，途中因交通堵塞停留了一段时间后，为了赶时间加快速度行驶．与以上事件吻合得最好的图象是(　　)‎ C　[距学校的距离应逐渐减小，由于小明先是匀速运动，故前段是直线段，途中停留时距离不变，后段加速，直线段比前段下降的快，故应选C.]‎ - 4 -‎ ‎4．如果f＝，则当x≠0,1时，f(x)等于(　　)‎ ‎【导学号：37102105】‎ A. B. C. D.－1‎ B　[令＝t，则x＝，代入f＝，则有f(t)＝＝，故选B.]‎ ‎5．若f(x)是一次函数，‎2f(2)－‎3f(1)＝5,‎2f(0)－f(－1)＝1，则f(x)＝(　　)‎ A．3x＋2 B．3x－2‎ C．2x＋3 D．2x－3‎ B　[设f(x)＝ax＋b，由题设有 解得所以选B.]‎ 二、填空题 ‎6．已知f(2x＋1)＝x2－2x，则f(3)＝________.‎ ‎－1　[由2x＋1＝3得x＝1，∴f(3)＝1－2＝－1.]‎ ‎7．如图124，函数f(x)的图象是折线段ABC，其中A，B，C的坐标分别为(0,4)，(2,0)，(6,4)，则f[f(0)]＝________. ‎ ‎【导学号：37102106】‎ 图124‎ ‎2　[由题意可知f(0)＝4，f(4)＝2，故f[f(0)]＝f(4)＝2.]‎ ‎8．某航空公司规定，乘客所携带行李的重量x(kg)与其运费y(元)由如图125的一次函数图象确定，那么乘客可免费携带行李的最大重量为________(kg)．‎ 图125‎ ‎19　[设一次函数解析式为y＝ax＋b(a≠0)，代入点(30,330)与点(40,630)得解得即y＝30x－570，若要免费，则y≤0，∴x≤19.]‎ 三、解答题 - 4 -‎ ‎9．画出二次函数f(x)＝－x2＋2x＋3的图象，并根据图象回答下列问题：‎ ‎(1)比较f(0)，f(1)，f(3)的大小．‎ ‎(2)求函数f(x)的值域. ‎ ‎【导学号：37102107】‎ ‎[解]　f(x)＝－(x－1)2＋4的图象如图所示：‎ ‎(1)f(0)＝3，f(1)＝4，f(3)＝0，‎ 所以f(1)>f(0)>f(3)．‎ ‎(2)由图象可知二次函数f(x)的最大值为f(1)＝4，‎ 则函数f(x)的值域为(－∞，4]．‎ ‎10．(1)已知f(x)是一次函数，且满足‎2f(x＋3)－f(x－2)＝2x＋21，求f(x)的解析式；‎ ‎(2)已知f(x)为二次函数，且满足f(0)＝1，f(x－1)－f(x)＝4x，求f(x)的解析式．‎ ‎(3)已知f＝x2＋＋1，求f(x)的解析式；‎ ‎[解]　(1)设f(x)＝ax＋b(a≠0)，‎ 则‎2f(x＋3)－f(x－2)＝2[a(x＋3)＋b]－[a(x－2)＋b]＝2ax＋‎6a＋2b－ax＋‎2a－b＝ax＋‎8a＋b＝2x＋21，‎ 所以a＝2，b＝5，所以f(x)＝2x＋5.‎ ‎(2)因为f(x)为二次函数，‎ 设f(x)＝ax2＋bx＋c(a≠0)．‎ 由f(0)＝1，得c＝1.‎ 又因为f(x－1)－f(x)＝4x，‎ 所以a(x－1)2＋b(x－1)＋c－(ax2＋bx＋c)＝4x，整理，得－2ax＋a－b＝4x，求得a＝－2，b＝－2，‎ 所以f(x)＝－2x2－2x＋1.‎ ‎(3)∵f＝2＋2＋1＝2＋3.∴f(x)＝x2＋3.‎ ‎[冲A挑战练]‎ ‎1．已知函数f(2x＋1)＝3x＋2，且f(a)＝2，则a的值为(　　) ‎ ‎【导学号：37102108】‎ A．－1 B．5‎ C．1 D．8‎ C　[由3x＋2＝2得x＝0，‎ 所以a＝2×0＋1＝1.故选C.]‎ - 4 -‎ ‎2．一等腰三角形的周长是20，底边长y是关于腰长x的函数，则它的解析式为(　　)‎ A．y＝20－2x B．y＝20－2x(0y，即2x>20－2x，即x>5，‎ 由y>0即20－2x>0得x<10，‎ 所以5