2020届高考文科数学二轮专题复习课件：专题5 解析几何2-5-高考小题 2 43页

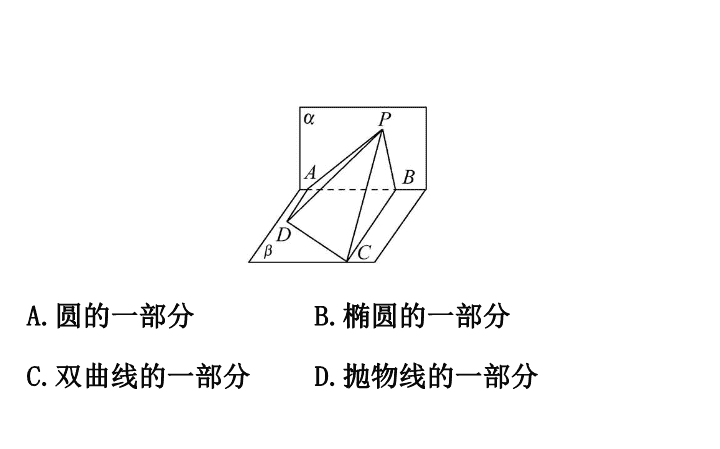
第 2 课时　 圆锥曲线的方程与性质 考向一　圆锥曲线的定义及标准方程 ( 保分题型考点 ) 【题组通关 】 1. 如图 ,△PAB 所在的平面 α 和四边形 ABCD 所在的平面 β 互相垂直 , 且 AD⊥α,BC⊥α,AD =4,BC=8,AB=6, 若 tan ∠ADP+2tan ∠BCP=10, 则点 P 在平面 α 内的轨迹 是 ( 　　 ) A. 圆的一部分 B. 椭圆的一部分 C. 双曲线的一部分 D. 抛物线的一部分 2. 已知 P 是抛物线 y 2 =4x 上的一个动点 ,Q 是圆 (x-3) 2 +(y-1) 2 =1 上的一个动点 ,N(1,0) 是一个定点 , 则 |PQ|+|PN| 的最小值为 ( 　　 ) A.3 B.4 C.5 D. +1 3.(2017 · 天津高考 ) 已知双曲线 =1(a>0,b>0) 的左焦点为 F, 离心率为 . 若经过 F 和 P(0,4) 两点的 直线平行于双曲线的一条渐近线 , 则双曲线的方程 为 ( 　　 ) 世纪金榜导学号 【解析 】 1. 选 B. 由题意可得 则 |PA|+|PB|=40>|AB|=6, 又因为 P,A,B 三点不共线 , 故点 P 的轨迹是以 A,B 为焦点的椭圆的一部分 . 2. 选 A. 由抛物线方程 y 2 =4x, 可得抛物线的焦点为 F(1,0), 又 N(1,0), 所以 N 与 F 重合 . 过圆 (x-3) 2 +(y-1) 2 =1 的圆心 M 作抛物线准线的垂线 MH, 交圆于 Q, 交抛物线于 P, 则 |PQ|+|PN| 的最小值等于 |MH|-1=3. 3. 选 B. 由题意得 a=b, =1⇒c=4,a=b=2 ⇒ 【拓展提升 】 1. 凡涉及抛物线上的点到焦点距离 , 一般运用定义转化为到准线的距离处理 . 如本例 (2) 充分运用抛物线定义实施转化 , 使解答简捷、明快 . 2. 求解圆锥曲线的标准方程的方法是“先定型 , 后计算” . 所谓“定型” , 就是指确定类型 , 所谓“计算” , 就是指利用待定系数法求出方程中的 a 2 ,b 2 ,p 的值 , 最后代入写出椭圆、双曲线、抛物线的标准方程 . 【变式训练 】 (1)(2016 · 天津高考 ) 已知双曲线 =1(a>0,b>0) 的焦距为 2 , 且双曲线的一条渐近线与直线 2x+y=0 垂直 , 则双曲线的方程为 ( 　　 ) A. -y 2 =1 B.x 2 - =1 C. =1 D. =1 (2)(2019 · 全国卷 Ⅲ) 设 F 1 ,F 2 为椭圆 C: =1 的两个焦点 ,M 为 C 上一点且在第一象限 . 若 △ MF 1 F 2 为等腰三角形 , 则 M 的坐标为 ________.  【解析 】 (1) 选 A. 由题意得 c= . 双曲线的渐近线为 y=± x, 因为渐近线与直线 2x+y=0 垂直 , 所以 (-2) · =-1, 所以 = . 又因为 c 2 =a 2 +b 2 , 解得 a=2,b=1, 所以双曲线的方程为 -y 2 =1. (2) 已知椭圆 C: =1 可知 ,a=6,c=4, 由 M 为 C 上 一点且在第一象限 , 故等腰 △ MF 1 F 2 中 , MF 1 =F 1 F 2 =8,MF 2 =2a-MF 1 =4,sin∠F 1 F 2 M= y M =MF 2 sin∠F 1 F 2 M= , 代入 C: =1 可得 x M =3. 故 M 的坐标为 (3, ). 答案 : (3, ) 考向二　圆锥曲线的几何性质 ( 保分题型考点 ) 【题组通关 】 1.(2019 · 全国卷 Ⅱ) 若抛物线 y 2 =2px(p>0) 的焦点是 椭圆 =1 的一个焦点 , 则 p= ( 　　 ) 　　　　　　 A.2 B.3 C.4 D.8 2.(2017 · 山东高考 ) 在平面直角坐标系 xOy 中 , 双曲线 =1(a>0,b>0) 的右支与焦点为 F 的抛物线 x 2 =2py(p>0) 交于 A,B 两点 , 若 |AF|+|BF|=4|OF|, 则该双 曲线的渐近线方程为 ________. 世纪金榜导学号   【解析 】 1. 选 D. 因为椭圆的焦点为 (± ,0), 抛物线 的焦点为 , 由已知可得 , 解得 p=8. 2. 设 A(x 1 ,y 1 ),B(x 2 ,y 2 ), 由抛物线的定义知 |AF|=y 1 + ,|BF|=y 2 + ,|OF|= , 所以 |AF|+|BF|=y 1 + +y 2 + =y 1 +y 2 +p=4|OF|=2p, 可得 y 1 +y 2 =p, 联立方程 得 +1=0, 由根与系数的 关系得 y 1 +y 2 = , 所以 =p, 则 , 所以双曲线的渐近线 方程为 y=± x. 答案 : y=± x 【拓展提升 】 1. 分析圆锥曲线中 a,b,c,e 各量之间的关系是求解圆锥曲线性质问题的关键 . 2. 确定椭圆和双曲线的离心率的值及范围 , 其关键就是确立一个关于 a,b,c 的方程 ( 组 ) 或不等式 ( 组 ), 再根据 a,b,c 的关系消掉 b 得到 a,c 的关系式 . 建立关于 a,b,c 的方程 ( 组 ) 或不等式 ( 组 ), 要充分利用椭圆和双曲线的几何性质、点的坐标的范围等 . 3. 求双曲线渐近线方程关键在于求 的值 , 也可将双曲线等号右边的“ 1” 变为“ 0”, 然后因式分解得到 . 【变式训练 】 (1) 已知 F 1 ,F 2 是双曲线 E: =1 的左、右焦点 , 点 M 在 E 上 ,MF 1 与 x 轴垂直 ,sin∠MF 2 F 1 = , 则 E 的 离心率为 ( 　　 ) (2)(2019 · 天津高考 ) 已知抛物线 y 2 =4x 的焦点为 F, 准 线为 l . 若 l 与双曲线 =1(a>0,b>0) 的两条渐近线 分别交于点 A 和点 B, 且 |AB|=4|OF|(O 为原点 ), 则双曲线 的离心率为 ( 　　 ) 【解析 】 (1) 选 A. 如图所示 , 设 M(-c,y ), 则 所以 y= , 在 Rt△MF 2 F 1 中 , sin∠MF 2 F 1 = 所以 a=b, 所以 e= (2) 选 D. l 的方程为 x=-1, 双曲线的渐近线方程为 y=± x, 可设 所以 |AB|= , 则 =4,b=2a, 所以 e= 考向三　圆锥曲线与其他知识的交汇问题 ( 压轴题型 考点 ) 【典例 】 （ 1 ）已知 M(x 0 ， y 0 ) 是双曲线 C ： 上的一点， F 1 ， F 2 是 C 的两个焦点．若 ① ， 则 y 0 的取值范围 ② 是（ ） （ 2 ）已知 l 是双曲线 C: =1 的一条渐近线， P 是 l 上的一点， F 1 ,F 2 是 C 的两个焦点，若 ③ ， 则 P 到 x 轴的距离 ④ 为世纪金榜导学号（ ） 【题眼直击 】 题目 题眼 思维导引 (1) ① 根据数量积公式建立不等关系 ② 解一元二次不等式 (2) ③ 根据数量积公式建立方程 ④ P 点纵坐标的大小即为所求 【解析 】 (1) 选 A. 由于点 M 在双曲线上 , 所以 即 =2 +2. 又因为 F 1 (- ,0),F 2 ( ,0), =(- -x 0 ,-y 0 ), =( -x 0 ,-y 0 ), 所以 · = + -3=3 -1<0, 解得 - b>0) 的左、右 顶点 , 不同两点 P,Q 在椭圆 C 上 , 且关于 x 轴对称 , 设直线 AP,BQ 的斜率分别为 m,n , 则当 +ln |m|+ ln |n| 取最小值时 , 椭圆 C 的离心率为 ( 　　 ) (2)(2019 · 全国卷 Ⅰ) 已知双曲线 C: =1 (a>0,b>0) 的左、右焦点分别为 F 1 ,F 2 , 过 F 1 的直线与 双曲线 C 的两条渐近线分别交于 A,B 两点 . 若 =0, 则 C 的离心率为 ________.  【解析 】 (1) 选 D. 设点 P(x 0 ,y 0 ), 则 所以 mn = 从而 +ln|m|+ln|n |= 设 =x, 令 f(x)= +ln x(0