2020版高中数学 第1章 解三角形章末分层突破学案 新人教B版必修5 10页

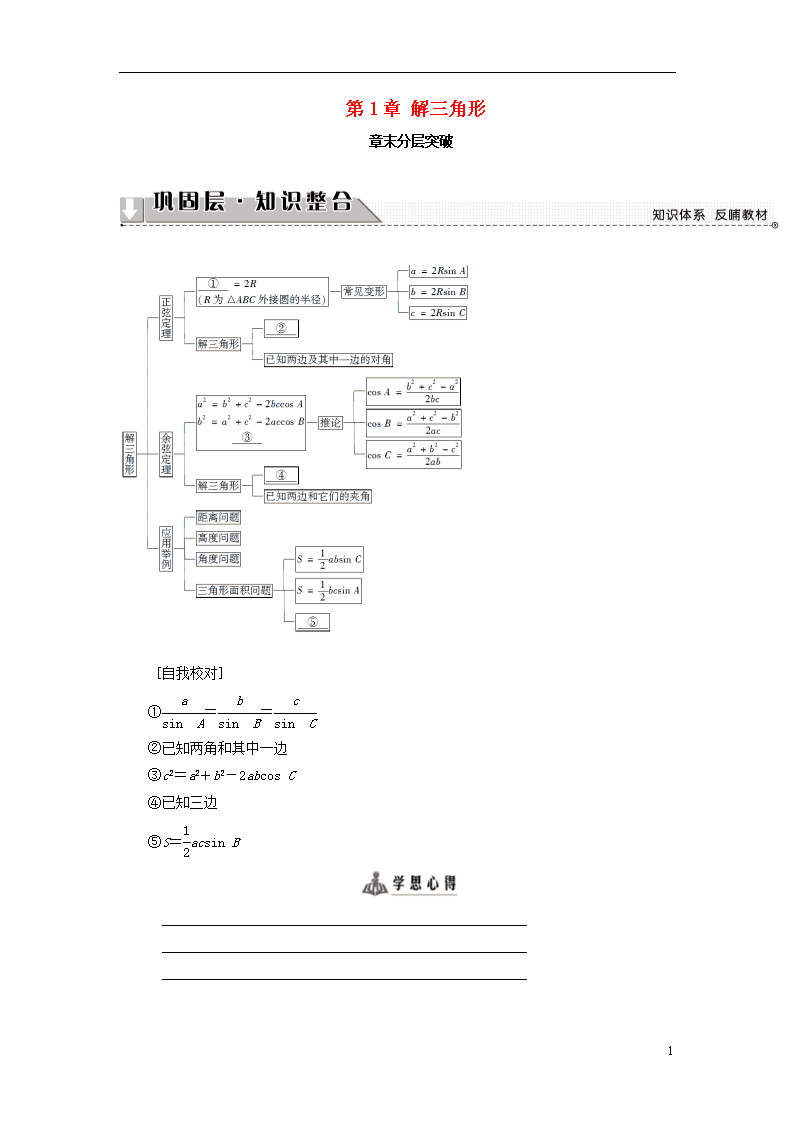
第1章 解三角形 章末分层突破 ‎ ‎ [自我校对]‎ ‎①＝＝ ‎②已知两角和其中一边 ‎③c2＝a2＋b2－2abcos C ‎④已知三边 ‎⑤S＝acsin B ‎　 ‎ ‎　 ‎ ‎　 ‎ 10‎ 利用正、余弦定理解三角形 解三角形就是已知三角形中的三个独立元素(至少一条边)求出其他元素的过程.三角形中的元素有基本元素(边和角)和非基本元素(中线、高、角平分线、外接圆半径和内切圆半径)，解三角形通常是指求未知的元素，有时也求三角形的面积.‎ 解斜三角形共包括四种类型：(1)已知三角形的两角和一边(一般先用内角和求角或用正弦定理求边)；(2)已知两边及夹角(一般先用余弦定理求第三边)；(3)已知三边(先用余弦定理求角)；(4)已知两边和一边的对角(先用正弦定理求另一边的对角或先用余弦定理求第三边，注意讨论解的个数).‎ ‎　△ABC的内角A，B，C的对边分别为a，b，c，asin A＋csin C－asin C＝bsin B.‎ ‎(1)求角B的大小；‎ ‎(2)若∠A＝75°，b＝2，求a，c.‎ ‎【精彩点拨】　(1)用正弦定理将已知关系式变形为边之间的关系，然后利用余弦定理求解.‎ ‎(2)先求角C，然后利用正弦定理求边a，c.‎ ‎【规范解答】　(1)由正弦定理得a2＋c2－ac＝b2.‎ 由余弦定理得b2＝a2＋c2－2accos B.‎ 故cos B＝，因此∠B＝45°.‎ ‎(2)sin A＝sin(30°＋45°)‎ ‎＝sin 30°cos 45°＋cos 30°sin 45°＝.‎ 故a＝b×＝1＋.‎ 由已知得，∠C＝180°－45°－75°＝60°，‎ c＝b×＝2×＝.‎ ‎[再练一题]‎ ‎1.在△ABC中，角A，B，C所对的边长分别为a，b，c，设a，b，c满足条件b2＋c2－bc＝a2和＝＋，求∠A和tan B的值. ‎ ‎【导学号：18082014】‎ 10‎ ‎【解】　由余弦定理cos A＝＝，因此∠A＝60°.在△ABC中，∠C＝180°－∠A－∠B＝120°－∠B.‎ 由已知条件，应用正弦定理 ＋＝＝＝ ‎＝ ‎＝＋，从而tan B＝.‎ 正、余弦定理的综合应用 正、余弦定理将三角形中的边和角关系进行了量化，为我们解三角形或求三角形的面积提供了依据，而三角形中的问题常与向量、函数、方程及平面几何相结合，通常可以利用正、余弦定理完成证明、求值等问题.‎ ‎(1)解三角形与向量的交汇问题，可以结合向量的平行、垂直、夹角、模等知识转化求解.‎ ‎(2)解三角形与其他知识的交汇问题，可以运用三角形的基础知识、正余弦定理、三角形面积公式与三角恒等变换，通过等价转化或构造方程及函数求解.‎ ‎　在△ABC中，角A，B，C的对边分别为a，b.c,4sin2－cos ‎2C＝，a＋b＝5，c＝.‎ ‎(1)求角C的大小；‎ ‎(2)求△ABC的面积.‎ ‎【精彩点拨】　(1)先降幂，转化成cos C的方程，求出cos C，进而求出角C；(2)由余弦定理列方程，得方程组，求出a，b，再求面积.‎ ‎【规范解答】　(1)由4sin2－cos ‎2C＝，‎ 得4cos2－cos ‎2C＝，‎ 所以4·－(2cos‎2C－1)＝.‎ 整理，得4cos‎2C－4cos C＋1＝0，‎ 解得cos C＝，‎ 所以∠C＝60°.‎ ‎(2)由余弦定理，得c2＝a2＋b2－2abcos C，‎ 即7＝a2＋b2－ab. ①‎ 10‎ 又因为a＋b＝5，所以a2＋b2＋2ab＝25. ②‎ ‎①②联立，解得ab＝6.‎ 所以S△ABC＝absin C＝×6×＝.‎ ‎[再练一题]‎ ‎2.△ABC的内角A，B，C的对边分别为a，b，c，已知2cos C(acos B＋bcos A)＝c.‎ ‎(1)求∠C；‎ ‎(2)若c＝，△ABC的面积为，求△ABC的周长.‎ ‎【解】　(1)由已知及正弦定理得 ‎2cos C(sin Acos B＋sin Bcos A)＝sin C，‎ 即2cos Csin(A＋B)＝sin C，‎ 故2sin Ccos C＝sin C.‎ 可得cos C＝，所以∠C＝.‎ ‎(2)由已知得absin C＝.‎ 又∠C＝，所以ab＝6.‎ 由已知及余弦定理得a2＋b2－2abcos C＝7，‎ 故a2＋b2＝13，从而(a＋b)2＝25.‎ 所以△ABC的周长为5＋.‎ 正、余弦定理的实际应用 正弦定理、余弦定理在实际生活中有着非常广泛的应用.常用的有测量距离问题，测量高度问题，测量角度问题等.解决的基本思路是画出正确的示意图，把已知量和未知量标在示意图中(目的是发现已知量与未知量之间的关系)，最后确定用哪个定理转化，用哪个定理求解，并进行作答，解题时还要注意近似计算的要求.‎ ‎　在某海滨城市附近海面有台风，据监测，当前台风中心位于城市O(如图11)的东偏南θ方向‎300 km的海面P处，并以‎20 km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域，当前半径为‎60 km，并以‎10 km/h的速度不断增大.问几小时后该城市开始受到台风的侵袭.‎ 10‎ 图11‎ ‎【精彩点拨】　设台风中心在t小时后由P到Q，所以在△OPQ中，OP＝300，∠OPQ＝θ－45°，PQ＝20t，可由余弦定理求出OQ.城市O受到台风的侵袭，需满足条件OQ≤10t＋60，然后通过解不等式求出城市O受到台风侵袭的时间.‎ ‎【规范解答】　设在时刻t(h)台风中心为Q，此时台风侵袭的圆形区域半径为(10t＋60)km，若在时刻t城市O受到台风的侵袭，则OQ≤10t＋60.‎ 由余弦定理，知 OQ2＝PQ2＋PO2－2PQ·POcos∠OPQ.‎ 因为PO＝‎300 km，PQ＝20t km，‎ cos∠OPQ＝cos(θ－45°)＝cos θcos 45°＋sin θsin 45°＝×＋×＝，‎ 所以OQ2＝(20t)2＋3002－2×20t×300× ‎＝202t2－9 600t＋3002.‎ 又因为OQ≤10t＋60，‎ 所以202t2－9 600t＋3002≤(10t＋60)2，‎ 即t2－36t＋288≤0，‎ 解得12≤t≤24.‎ 所以12个小时后该城市开始受到台风的侵袭.‎ ‎[再练一题]‎ ‎3.如图12，某住宅小区的平面图呈扇形AOC.小区的两个出入口设置在点A及点C处，小区里有两条笔直的小路AD，DC，且拐弯处的转角为120°.已知某人从C沿CD走到D用了10分钟，从D沿DA走到A用了6分钟.若此人步行的速度为每分钟‎50米，求该扇形的半径OA的长(精确到‎1米).‎ 图12‎ ‎【解】　法一：设该扇形的半径为r米，由题意，得CD＝‎500米，DA＝‎300米，∠CDO＝60°.‎ 在△CDO中，CD2＋OD2－2·CD·OD·cos 60°＝OC2，‎ 即5002＋(r－300)2－2×500×(r－300)×＝r2，‎ 10‎ 解得r＝≈445(米).‎ 法二：连接AC，作OH⊥AC，交AC于点H，‎ 由题意，得CD＝‎500米，AD＝‎300米，∠CDA＝120°.‎ 在△ACD中，AC2＝CD2＋AD2－2·CD·AD·cos 120°＝5002＋3002＋2×500×300×＝7002，‎ ‎∴AC＝700(米).‎ cos∠CAD＝＝.‎ 在Rt△HAO中，AH＝350(米)，cos∠HAO＝，‎ ‎∴OA＝＝≈445(米).‎ 三角形形状的判断 一般来说，判断三角形的形状问题常用的方法有两种：(1)通过边之间的关系判断形状；(2)通过角之间的关系判断形状.正弦定理、余弦定理在解题中起到将已知条件中的边、角互化，把条件化为边之间的关系或化为角之间的关系的作用.‎ ‎　在△ABC中，已知∠B＝60°，2b＝a＋c，试判断△ABC的形状.‎ ‎【精彩点拨】　通过正弦定理，把2b＝a＋c化边为角判断或通过余弦定理，利用cos B＝化角为边判断.‎ ‎【规范解答】　法一：由正弦定理，得2sin B＝sin A＋sin C.‎ 因为∠B＝60°，所以∠A＋‎ ‎∠C＝120°，‎ 所以∠A＝120°－∠C.‎ 代入上式，得2sin 60°＝sin(120°－C)＋sin C.‎ 整理，得sin C＋cos C＝1，‎ 即sin(C＋30°)＝1.‎ 所以∠C＋30°＝90°，∠C＝60°.‎ 所以∠A＝60°.‎ 所以△ABC为等边三角形.‎ 法二：由余弦定理，得b2＝a2＋c2－2accos B.‎ 代入b＝(a＋c)，得(a＋c)2＝a2＋c2－‎2ac·.‎ 化简，得a2＋c2－‎2ac＝0，‎ 即(a－c)2＝0，‎ 所以a＝c，△ABC为等腰三角形.‎ 10‎ 又因为∠B＝60°，‎ 所以△ABC为等边三角形.‎ ‎[再练一题]‎ ‎4.在△ABC中，若sin A＋cos A＝，则这个三角形是(　　)‎ A.钝角三角形 B.直角三角形 C.锐角三角形 D.等边三角形 ‎【解析】　法一：若∠A≤90°，则sin A＋cos A＝sin(A＋45°)≥1＞，∴∠A＞90°，故选A.‎ 法二：∵sin A＋cos A＝，‎ ‎∴(sin A＋cos A)2＝，‎ ‎∴1＋2sin A·cos A＝，‎ ‎∴sin A·cos A＝－＜0.‎ ‎∵0°＜∠A＜180°，sin A＞0，‎ ‎∴cos A＜0,90°＜∠A＜180°，故选A.‎ ‎【答案】　A 转化与化归思想 转化与化归思想用于研究、解决数学问题时思维受阻或寻求简单方法的情况下，把一种状况转化为另一种状况，也就是转化为另一种情境，使问题得到解决，这种转化是解决问题的有效策略，同时也是成功的思维方式.‎ 本章主要是综合运用正、余弦定理解决较为复杂的与解三角形有关的问题，在判断三角形的形状的问题中，利用边、角之间的转化与化归的方法是解决这类问题的基本思路.‎ ‎　在△ABC中，已知(a＋b＋c)(a＋b－c)＝3ab，且2cos Asin B＝sin C，试确定△ABC的形状.‎ ‎【精彩点拨】　充分运用正弦定理和余弦定理，可利用边的关系判断，也可转化为角的关系来判断.‎ ‎【规范解答】　法一：由正弦定理，得＝.‎ 又2cos Asin B＝sin C，所以cos A＝＝.‎ 由余弦定理，有cos A＝.‎ 10‎ 所以＝，即c2＝b2＋c2－a2.‎ 所以a＝b.‎ 又因为(a＋b＋c)(a＋b－c)＝3ab，‎ 所以(a＋b)2－c2＝3ab，所以4b2－c2＝3b2.‎ 所以b＝c，所以a＝b＝c.‎ 因此△ABC为等边三角形.‎ 法二：因为∠A＋∠B＋∠C＝180°，所以sin C＝sin(A＋B).‎ 又因为2cos Asin B＝sin C，‎ 所以2cos Asin B＝sin Acos B＋cos Asin B，‎ 所以sin(A－B)＝0.‎ 因为∠A、∠B均为三角形的内角，所以∠A＝∠B.‎ 又由(a＋b＋c)(a＋b－c)＝3ab.‎ 得(a＋b)2－c2＝3ab，即a2＋b2－c2＝ab.‎ 所以cos C＝＝＝.‎ 因为0°<∠C<180°，所以∠C＝60°.‎ 因此△ABC为等边三角形.‎ ‎[再练一题]‎ ‎5.已知△ABC中，＝c2，且acos B＝bcos A，试判断△ABC的形状.‎ ‎【解】　由＝c2，得a3＋b3－c3＝c2(a＋b)－c3，‎ ‎∴a2＋b2－ab＝c2，∴cos C＝，∴∠C＝60°.‎ 由acos B＝bcos A，得2Rsin Acos B＝2Rsin Bcos A(R为△ABC外接圆的半径)，‎ ‎∴sin(A－B)＝0，∴∠A－∠B＝0，‎ ‎∴∠A＝∠B＝∠C＝60°，∴△ABC为等边三角形.‎ ‎1.△ABC的内角A，B，C的对边分别为a，b，c，已知a＝，c＝2，cos A＝，则b＝(　　)‎ A.　　　　B.　　　　C.2　　　　D.3‎ 10‎ ‎【解析】　由余弦定理得5＝b2＋4－2×b×2×，‎ 解得b＝3或b＝－(舍去)，故选D.‎ ‎【答案】　D ‎2.△ABC中，角A，B，C的对边分别是a，b，c.已知b＝c，a2＝2b2(1－sin A)，则∠A＝(　　)‎ A. B. C. D. ‎【解析】　∵b＝c，∴∠B＝∠C.‎ 又由∠A＋∠B＋∠C＝π得∠B＝－.‎ 由正弦定理及a2＝2b2(1－sin A)得 sin‎2A＝2sin2B(1－sin A)，‎ 即sin‎2A＝2sin2(1－sin A)，‎ 即sin‎2A＝2cos2(1－sin A)，‎ 即4sin2cos2＝2cos2(1－sin A)，‎ 整理得cos2＝0，‎ 即cos2(cos A－sin A)＝0.‎ ‎∵0<∠A<π，∴0<<，∴cos ≠0，‎ ‎∴cos A＝sin A.‎ 又0<∠A<π，∴A＝.‎ ‎【答案】　C ‎3.在△ABC中，∠A＝，a＝c，则＝________.‎ ‎【解析】　在△ABC中，∠A＝，‎ ‎∴a2＝b2＋c2－2bccos，即a2＝b2＋c2＋bc.‎ ‎∵a＝c，∴‎3c2＝b2＋c2＋bc，∴b2＋bc－‎2c2＝0，‎ ‎∴(b＋‎2c)(b－c)＝0，∴b－c＝0，∴b＝c，∴＝1.‎ ‎【答案】　1‎ 10‎ ‎4.在△ABC中，内角A，B，C所对应的边分别为a，b，c.已知asin 2B＝bsin A.‎ ‎(1)求∠B；‎ ‎(2)若cos A＝，求sin C的值.‎ ‎【解】　(1)在△ABC中，由＝，‎ 可得asin B＝bsin A.‎ 又由asin 2B＝bsin A，得 ‎2asin Bcos B＝bsin A＝asin B，‎ 所以cos B＝，所以∠B＝.‎ ‎(2)由cos A＝，可得sin A＝，则 sin C＝sin[π－(A＋B)]＝sin(A＋B)＝sin ‎＝sin A＋cos A＝.‎ ‎5.在△ABC中，内角A，B，C所对的边分别为a，b，c.已知b＋c＝2acos B.‎ ‎(1)证明：∠A＝2∠B；‎ ‎(2)若cos B＝，求cos C的值.‎ ‎【解】　(1)证明：由正弦定理得sin B＋sin C＝2sin Acos B，‎ 故2sin Acos B＝sin B＋sin(A＋B)＝sin B＋sin Acos B＋cos Asin B，于是sin B＝sin(A－B).‎ 又∠A，∠B∈(0，π)，故0<∠A－∠B<π，所以∠B＝π－(∠A－∠B)或∠B＝∠A－∠B，因此，∠A＝π(舍去)或∠A＝2∠B，所以∠A＝2∠B.‎ ‎(2)由cos B＝得sin B＝，cos 2B＝2cos2B－1＝－，故cos A＝－，sin A＝，‎ cos C＝－cos(A＋B)＝－cos Acos B＋sin Asin B＝.‎ 10‎