2015年数学理高考课件1-2 命题及其关系、充分条件与必要条件 31页

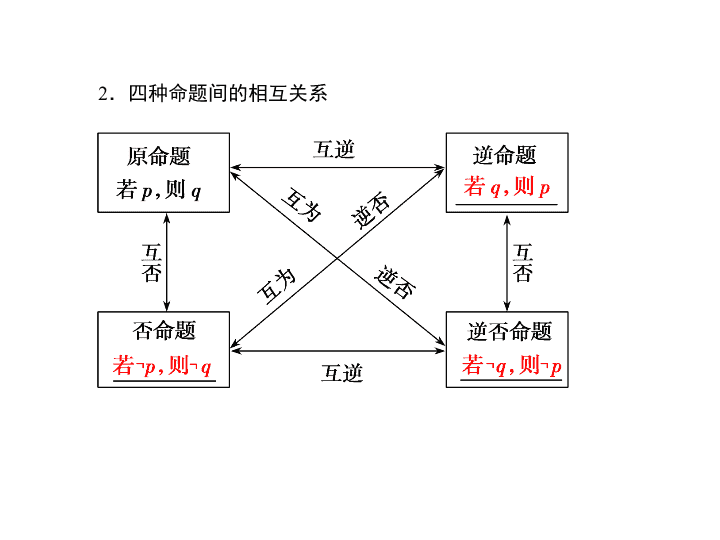
[ 最新考纲展示 ] 　 1 ． 理解命题的概念．　 2. 了解 “ 若 p ，则 q ” 形式的命题及其逆命题、否命题与逆否命题，会分析四种命题的相互关系． 3 ．理解必要条件、充分条件与充要条件的意义 . 第二节　命题及其关系、充分条件与必要条件 四种命题及其关系 1 ．命题的概念 在数学中用语言、符号或式子表达的，可以 的陈述句叫做命题．其中 的语句叫做真命题， 的语句叫做假命题． 判断真假 判断为真 判断为假 2 ．四种命题间的相互关系 3 ．四种命题的真假关系 原命题 逆命题 否命题 逆否命题 真 真 真 真 真 假 假 真 假 真 真 假 假 假 假 假 由上表可知： (1) 两个命题互为逆否命题，它们有 的真假性； (2) 两个命题互为逆命题或互为否命题，它们的真假性 ． 相同 没有关系 ____________________[ 通关方略 ]____________________ 1 ．区别 “ 否命题 ” 与命题的否定：否命题是既否定命题的条件，又否定命题的结论，而命题的否定是只否定命题的结论，要注意区别． 2 ．由于互为逆否命题的两个命题具有相同的真假性，因而当判断一个命题的真假比较困难时，可转化为判断它的逆否命题的真假． 1 ．已知 a ， b ， c ∈ R ，命题 “ 若 a ＋ b ＋ c ＝ 3 ，则 a 2 ＋ b 2 ＋ c 2 ≥3 ” 的否命题是 ( 　　 ) A ．若 a ＋ b ＋ c ≠3 ，则 a 2 ＋ b 2 ＋ c 2 <3 B ．若 a ＋ b ＋ c ＝ 3 ，则 a 2 ＋ b 2 ＋ c 2 <3 C ．若 a ＋ b ＋ c ≠3 ，则 a 2 ＋ b 2 ＋ c 2 ≥3 D ．若 a 2 ＋ b 2 ＋ c 2 ≥3 ，则 a ＋ b ＋ c ＝ 3 解析： a ＋ b ＋ c ＝ 3 的否定是 a ＋ b ＋ c ≠3 ， a 2 ＋ b 2 ＋ c 2 ≥ 3 的否定是 a 2 ＋ b 2 ＋ c 2 <3. 答案： A 2 ．下列命题中为真命题的是 ( 　　 ) A ．命题 “ 若 x > y ，则 x >| y | ” 的逆命题 B ．命题 “ x >1 ，则 x 2 >1 ” 的否命题 C ．命题 “ 若 x ＝ 1 ，则 x 2 ＋ x － 2 ＝ 0 ” 的否命题 D ．命题 “ 若 x 2 >0 ，则 x >1 ” 的逆否命题 解析： 对于 A ，其逆命题是：若 x >| y | ，则 x > y ，是真命题，这是因为 x >| y | ≥ y ，必有 x > y ；对于 B ，否命题是：若 x ≤ 1 ，则 x 2 ≤ 1 ，是假命题．如 x ＝－ 5 ， x 2 ＝ 25>1 ；对于 C ，其否命题是：若 x ≠1 ，则 x 2 ＋ x － 2≠0 ，由于 x ＝－ 2 时， x 2 ＋ x － 2 ＝ 0 ，所以是假命题；对于 D ，若 x 2 >0 ，则 x >0 或 x <0 ，不一定有 x >1 ，因此原命题的逆否命题是假命题． 答案： A 充分条件与必要条件 1 ．如果 p ⇒ q ，则 p 是 q 的 ， q 是 p 的 ． 2 ．如果 p ⇒ q ， q ⇒ p ，则 p 是 q 的 ． 充分条件 必要条件 充要条件 ____________________[ 通关方略 ]____________________ 如何判断 p 是 q 的什么条件？ 1 ．对命题 “ 若 p ，则 q ” ，首先应分清条件是什么 ( p ) ，结论是什么 ( q ) ． 2 ．尝试用条件推结论，再尝试用结论推条件，推理方法可以用直接证明法或间接证明法． 3 ．确定条件是结论的什么条件，抓住 “ 以小推大 ” 的技巧，即小范围推得大范围． 4 ．判断的结论需分四种情况：充分不必要条件、必要不充分条件、充要条件、既不充分也不必要条件． 3 ．若 a ∈ R ，则 “ a ＝ 1 ” 是 “ | a | ＝ 1 ” 的 ( 　　 ) A ．充分而不必要条件　　 B ．必要而不充分条件 C ．充要条件 D ．既不充分也不必要条件 解析： 若 a ＝ 1 ，则有 | a | ＝ 1 是真命题，即 a ＝ 1 ⇒ | a | ＝ 1 ，由 | a | ＝ 1 可得 a ＝ ±1 ，所以若 | a | ＝ 1 ，则有 a ＝ 1 是假命题，即 | a | ＝ 1 ⇒ a ＝ 1 不成立，所以 a ＝ 1 是 | a | ＝ 1 的充分而不必要条件． 答案： A 4 ．设集合 A ＝ { x ∈ R | x － 2>0} ， B ＝ { x ∈ R | x <0} ， C ＝ { x ∈ R | x ( x － 2)>0} ，则 “ x ∈ A ∪ B ” 是 “ x ∈ C ” 的 ( 　　 ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件 解析： 由题意得 A ∪ B ＝ { x ∈ R | x <0 或 x >2} ， C ＝ { x ∈ R | x <0 或 x >2} ，故 A ∪ B ＝ C ，则 “ x ∈ A ∪ B ” 是 “ x ∈ C ” 的充要条件． 答案： C 四种命题及其真假判断 【 例 1】 　 (2014 年南京模拟 ) 有下列几个命题： ① “ 若 a > b ，则 a 2 > b 2 ” 的否命题； ② “ 若 x ＋ y ＝ 0 ，则 x ， y 互为相反数 ” 的逆命题； ③ “ 若 x 2 <4 ，则－ 2< x <2 ” 的逆否命题． 其中真命题的序号是 ________ ． [ 解析 ] 　 ① 原命题的否命题为 “ 若 a ≤ b 则 a 2 ≤ b 2 ” 错误． ② 原命题的逆命题为： “ 若 x ， y 互为相反数，则 x ＋ y ＝ 0 ” 正确． ③ 原命题的逆否命题为 “ 若 x ≥ 2 或 x ≤ － 2 ，则 x 2 ≥ 4 ” 正确． [ 答案 ] 　 ②③ 反思总结 1 ． 要注意四种命题关系的相对性，一旦一个命题定为原命题，也就相应地确定了它的 “ 逆命题 ” 、 “ 否命题 ” 、 “ 逆否命题 ” ． 2 ．判断命题真假时，可直接依据定义、定理、性质直接判断，也可使用特值进行排除． 答案： D 充分条件和必要条件的判定 【 例 2】 　 (2013 年高考湖南卷 )“1< x <2” 是“ x <2” 成立的 ( 　　 ) A ．充分不必要条件　　　 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 [ 解析 ] 　 当 1< x <2 时， x <2 成立；当 x <2 时， 1< x <2 不一定成立，所以 “ 1< x <2 ” 是 “ x <2 ” 成立的充分不必要条件． [ 答案 ] 　 A 反思总结 判断充分条件与必要条件的策略 (1) 寻求 q 的必要条件 p ，即以 q 为条件推出结论 p ； (2) 寻求 q 的充分条件 p ，即求使 q 成立的条件 p ； (3) 寻求 q 的充要条件 p ，从上述两方面入手，若得到的结论都正确，则 p 为 q 的充要条件． 变式训练 2 ． “ a ＋ c > b ＋ d ” 是 “ a > b 且 c > d ” 的 ( 　　 ) A ．充分不必要条件　　　　 B ．既不充分也不必要条件 C ．充分必要条件 D ．必要不充分条件 解析： 由 “ a ＋ c > b ＋ d ” 不能得知 “ a > b 且 c > d ” ，反过来，由 “ a > b 且 c > d ” 可得知 “ a ＋ c > b ＋ d ” ，因此 “ a ＋ c > b ＋ d ” 是 “ a > b 且 c > d ” 的必要不充分条件，选 D. 答案： D 充要条件的应用 【 例 3 】 　 已知 P ＝ { x | x 2 － 8 x － 20≤0} ， S ＝ { x |1 － m ≤ x ≤1 ＋ m } ． (1) 是否存在实数 m ，使 x ∈ P 是 x ∈ S 的充要条件，若存在，求出 m 的范围； (2) 是否存在实数 m ，使 x ∈ P 是 x ∈ S 的必要条件，若存在，求出 m 的范围． 反思总结 解决与充要条件有关的参数问题的方法：解决此类问题一般是把充分条件、必要条件或充要条件转化为集合之间的关系，然后根据集合之间的关系列出关于参数的不等式求解． 答案： D —— 与充要条件有关的交汇问题 充分条件、必要条件和充要条件的判断是高考的热点内容、多与函数、不等式、向量、立体几何、解析几何等知识交汇命题． 与函数不等式有关的交汇命题 【 典例 1 】 　 (2013 年高考安徽卷 ) “ a ≤0 ” 是 “ 函数 f ( x ) ＝ |( ax － 1) x | 在区间 (0 ，＋∞ ) 内单调递增 ” 的 ( 　　 ) A ．充分不必要条件　　　 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 [ 答案 ] 　 C 由题悟道 该题处理的关键是将函数 f ( x ) 在 (0 ，＋∞ ) 内递增等价转化为方程 f ( x ) ＝ 0 在 (0 ，＋∞ ) 内无实根，通常与函数、不等式相关的充要性判断问题多是先求解命题的充要条件，再进行判断． 与三角、向量有关的交汇命题 【 典例 2 】 　 (2013 年高考陕西卷 ) 设 a ， b 为向量，则 “ | a · b | ＝ | a || b | ” 是 “ a ∥ b ” 的 ( 　　 ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 [ 解析 ] 　 从数量积入手，设 α 为向量 a ， b 的夹角，则 | a · b | ＝ | a || b | · |cos α | ＝ | a || b | ⇔ |cos α | ＝ 1 ⇔ cos α ＝ ±1 ⇔ 向量 a ， b 共线． [ 答案 ] 　 C 由题悟道 解决三角与向量的相关的充要性问题，多是抓住相关的概念、性质、结论去直接判断． 与立体几何、解析几何有关的交汇命题 【 典例 3 】 　 (2014 年西安模拟 ) 若设平面 α 、平面 β 相交于直线 m ，直线 a 在平面 α 内，直线 b 在平面 β 内，且 b ⊥ m ，则 “ α ⊥ β ” 是 “ a ⊥ b ” 的 ( 　　 ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件 [ 解析 ] 　 由 α ⊥ β 和 b ⊥ m ，知 b ⊥ α ，又 a ⊂ α ， ∴ a ⊥ b ， “ α ⊥ β ” 可以推出 “ a ⊥ b ” ，反过来，不一定能推出，即 “ α ⊥ β ” 是 “ a ⊥ b ” 的充分不必要条件． [ 答案 ] 　 A 由题悟道 抓住立体几何中的判定定理与性质定理成立的条件去判断分析是解此类题的关键，要注意结合图形． 答案： A 2 ． “ m ＝－ 1 ” 是 “ 直线 mx ＋ (2 m － 1) y ＋ 2 ＝ 0 与直线 3 x ＋ my ＋ 3 ＝ 0 垂直 ” 的 ( 　　 ) A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．即不充分也不必要条件 解析： 由 m × 3 ＋ (2 m － 1) × m ＝ 0 ∴ 3 m ＋ 2 m 2 － m ＝ 0 ∴ m ＝ 0 或－ 1 故 m ＝－ 1 是两线垂直的充分不必要条件． 答案： A 本小节结束 请按 ESC 键返回