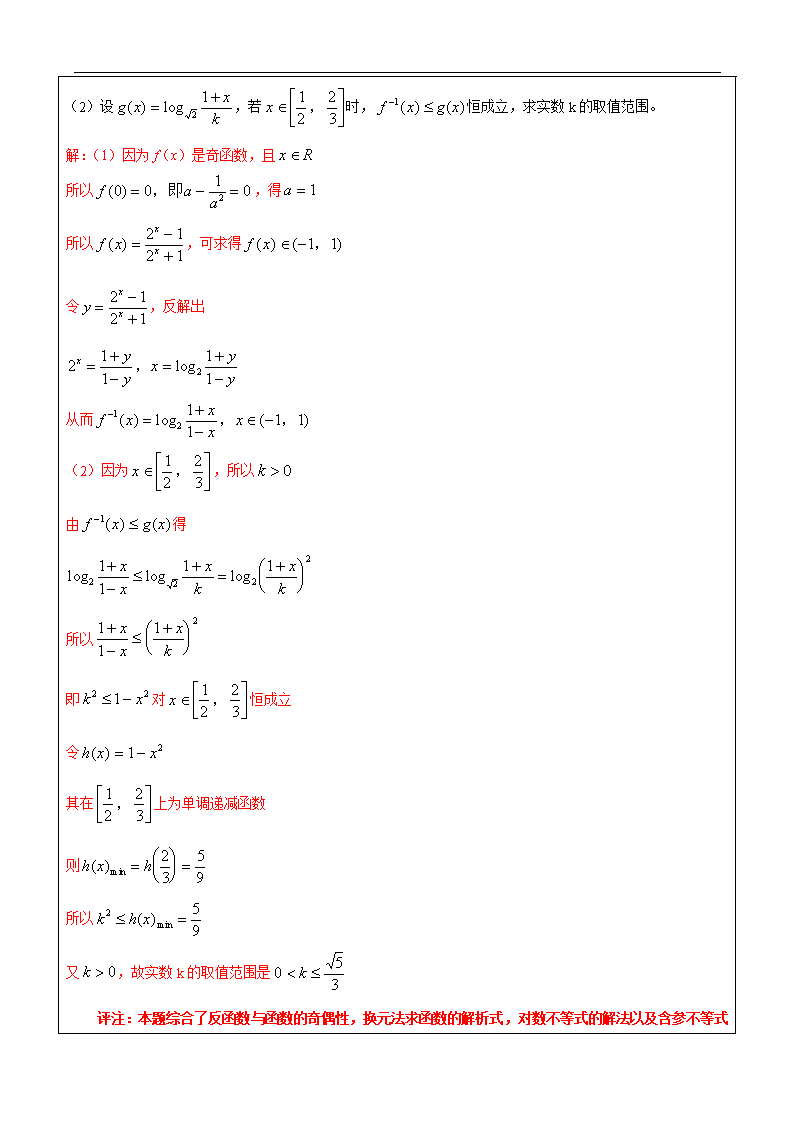高一数学教案：第2讲 对数函数综合 7页

辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目： ‎ 授课日期 ‎××年××月××日 ‎ 时 间 A / B / C / D / E / F段 主 题 对数函数综合 教学内容 ‎1. 熟练掌握对数函数的性质；‎ ‎2. 会应用对数函数的图像与性质解决综合问题。‎ ‎（以提问的形式回顾）‎ ‎1. 解决与对数函数有关的问题,有哪些需要注意的地方？‎ 解决与对数函数有关的问题，要特别重视定义域，同时注意底数与1的大小关系 ‎2. 底数互为倒数的两个对数函数的图像有什么特点？‎ 底数互为倒数的两个对数函数的图像关于轴对称 ‎3. 已知在上是的减函数，则的取值范围是什么？‎ 由于 在上时 有意义，又是减函数，∴时，取最小值是，∴综上可知所求的取值范围是。‎ 此部分让学生回答，如出现学生不会的问题，可相互讨论，结合教师引导，5到10分钟完成。‎ ‎（采用教师引导，学生轮流回答的形式）‎ 例1.在函数中，若函数在内为增函数，则实数的取值范围是 .‎ 答案：. 注意隐含条件函数在内都都大于0.‎ 试一试：若函数在区间上是增函数，则的取值范围是 。‎ 答案：‎ 例2. 若函数的定义域为，则的取值范围是 .‎ 解：当时，满足题意；当时，有，解得，‎ 所以的取值范围是．‎ 试一试：若函数的值域为，则的取值范围是 .‎ 由 得，所以的取值范围是 例3. 设不等式时，求的最大值和最小值．‎ 解： ‎ 即 ‎∴即 又 ‎∵∴ ‎ ‎∴当即时；当，即时，。‎ ‎【利用换元的整体思想，将视为一个整体。】‎ 例4. 设，f（x）是奇函数，且。‎ ‎（1）试求f（x）的反函数f－1（x）的解析式及f－1（x）的定义域；‎ ‎（2）设，若时，恒成立，求实数k的取值范围。‎ 解：（1）因为f（x）是奇函数，且 所以，得 所以，可求得 令，反解出 从而 ‎（2）因为，所以 由得 所以 即对恒成立 令 其在上为单调递减函数 则 所以 又，故实数k的取值范围是 评注：本题综合了反函数与函数的奇偶性，换元法求函数的解析式，对数不等式的解法以及含参不等式在定区间上恒成立等知识，是一道综合性较强的好题。‎ ‎（学生统一完成，互相批改，教师针对重难点详细讲解）‎ ‎1. 已知是上的增函数，那么的取值范围是( ) D ‎(A) ； (B) ； (C) ； (D) ．‎ ‎2. 已知函数，若，且，则的取值范围是________．‎ ‎3. 已知 ‎(1) 求函数的定义域和值域； (2) 判断函数在定义域上的单调性．‎ 分析：解指数不等式可得定义域，再求值域；先利用特值判断单调性再利用定义证明即可．‎ 解：（1）由且，解得，故的定义域为；‎ 又，，即，‎ 的值域为．‎ ‎（2）在上是单调减函数，证明如下：设，则：‎ ‎，‎ ‎，则，即，，‎ 故函数在上是减函数．‎ 利用定义来证明函数的单调性，注意步骤要完整；解不等式时要注意原函数的定义域的限制．‎ ‎4. 已知函数.‎ ‎（1）当m=7时，求函数f（x）的定义域；‎ ‎（2）若关于x的不等式f（x）≥2的解集是R，求m的取值范围．‎ 解：（1）由题设知：当m=5时：|x+1|+|x﹣2|＞7，‎ 不等式的解集是以下三个不等式组解集的并集：‎ ‎， 或， 或，‎ 解得函数f（x）的定义域为（﹣∞，﹣3）∪（4，+∞）；‎ ‎（2）不等式f（x）≥2即|x+1|+|x﹣2|≥m+4， ∵x∈R时，恒有|x+1|+|x﹣2|≥|（x+1）﹣（x﹣2）|=3，‎ ‎∴不等式|x+1|+|x﹣2|≥m+4解集是R，等价于m+4≤3， ∴m的取值范围是（﹣∞，﹣1]．‎ ‎ ‎ 本节课主要知识：复合函数单调区间的确定与应用，应用换元发求解函数的最大值，最小值 ‎【巩固练习】‎ 1． 已知函数当时，函数的零点 . ‎ ‎2. 已知函数的定义域为R，值域为[0，2]，求m,n的值 由，得，即.‎ ‎ ∵，即。由0，得 ‎，由根与系数的关系得，解得m=n=5。‎ ‎3. 设 ‎（1）当m=1时，求函数f（x）的定义域；‎ ‎（2）若当恒成立，求实数m的取值范围．‎ 解：（1）由题设知：， ‎ ‎∴ ①，或 ②，或 ③．‎ 解①可得 ，解②可得，解③可得 x＜0．‎ 不等式的解集是以下三个不等式组解集的并集，求得函数的定义域为 （﹣∞，0）∪（5，+∞）．‎ ‎（2）不等式 即，即.‎ ‎∵，∴，即 ．‎ 由于函数 在[1，]上是增函数，故当x=1时，y 取得最小值为4；‎ 当时，y 取得最大值为13， 由题意可得，m大于或等于y的最大值13，故m的取值范围是[13，+∞）．‎ ‎【预习思考】‎ 类型 指数方程的解法 对数方程的解法 最简型 关于x 的方程的解为 .‎ 关于x 的方程的解为 .‎ 同底型 与 ‎ 方程是同解方程 与 ‎ 方程是同解方程 换元型 关于x 的方程，设 ，解方程 =0，再解方程 关于x 的方程，设 ，解方程 =0，再解方程