2020高中数学 课时分层作业6 曲线与方程 新人教A版选修2-1 5页

课时分层作业(六) 曲线与方程 ‎(建议用时：40分钟)‎ ‎[基础达标练]‎ 一、选择题 ‎1．“曲线C上的点的坐标都是方程f(x，y)＝0的解”是“曲线C的方程是f(x，y)＝‎0”‎的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 B　[“曲线C的方程是f(x，y)＝‎0”‎包括“曲线C上的点的坐标都是方程f(x，y)＝0的解”和“以方程f(x，y)＝0的解为坐标的点都在曲线C上”两个方面，所以“曲线C上的点的坐标都是方程f(x，y)＝0的解”是“曲线C的方程是f(x，y)＝‎0”‎的必要不充分条件，故选B.]‎ ‎2．方程y＝－表示的曲线是(　　)‎ A．一个圆　　　　 B．一条射线 C．半个圆 D．一条直线 C　[方程y＝－可化为x2＋y2＝3(y≤0)，故选C.]‎ ‎3．在平面直角坐标系xOy中，点B与点A(－1,1)关于原点O对称，P是动点，且直线AP与BP的斜率之积等于－，则动点P的轨迹方程为(　　)‎ A．x2－3y2＝4‎ B．x2＋3y2＝4‎ C．x2－3y2＝4(x≠±1)‎ D．x2＋3y2＝4(x≠±1)‎ D　[由点B与点A(－1,1)关于原点对称，得点B的坐标为(1，－1)．设点P的坐标为(x，y)，由题意得kAP·kBP＝·＝－(x≠±1)，化简得x2＋3y2＝4，且x≠±1.故动点P的轨迹方程为x2＋3y2＝4(x≠±1)．]‎ ‎4．已知点P是直线x－2y＋3＝0上的一个动点，定点M(－1，2)，Q是线段PM延长线上的一点，且|PM|＝|MQ|，则点Q的轨迹方程是(　　) ‎ ‎【导学号：46342056】‎ A．x＋2y＋3＝0　 B．x－2y－5＝0‎ C．x－2y－7＝0 D．x－2y＋7＝0‎ 5‎ D　[设P(x0，y0)，则x0－2y0＋3＝0　(*)．又设Q(x，y)，由|PM|＝|MQ|，知点M是线段PQ的中点，则，即(**)．将(**)代入(*)，得(－2－x)－2(4－y)＋3＝0，即x－2y＋7＝0.故选D.]‎ ‎5．设点A为圆(x－1)2＋y2＝1上的动点，PA是圆的切线，且|PA|＝1，则P点的轨迹方程为(　　)‎ A．y2＝2x B．(x－1)2＋y2＝4‎ C．y2＝－2x D．(x－1)2＋y2＝2‎ D　[如图，设P(x，y)，圆心为M(1,0)．连接MA，则MA⊥PA，且|MA|＝1，‎ 又∵|PA|＝1，‎ ‎∴|PM|＝ ‎＝.‎ 即|PM|2＝2，‎ ‎∴(x－1)2＋y2＝2.]‎ 二、填空题 ‎6．方程(x－1)2＋＝0表示的是________．‎ 点(1,2)　[由题意知，，即 所以方程(x－1)2＋＝0表示点(1,2)．]‎ ‎7．设命题甲：点P的坐标适合方程f(x，y)＝0，命题乙：点P在曲线C上，命题丙：点Q坐标不适合f(x，y)＝0，命题丁：点Q不在曲线C上，已知甲是乙的必要条件，但不是充分条件，那么丙是丁的________条件．‎ 充分不必要条件　[由甲是乙的必要不充分条件知，曲线C是方程f(x，y)＝0的曲线的一部分，则丙⇒丁，但丁D⇒/丙，因此丙是丁的充分不必要条件．]‎ ‎8．已知定点F(1,0)，动点P在y轴上运动，点M在x轴上，且·＝0，延长MP到点N，使得||＝||，则点N的轨迹方程是________. 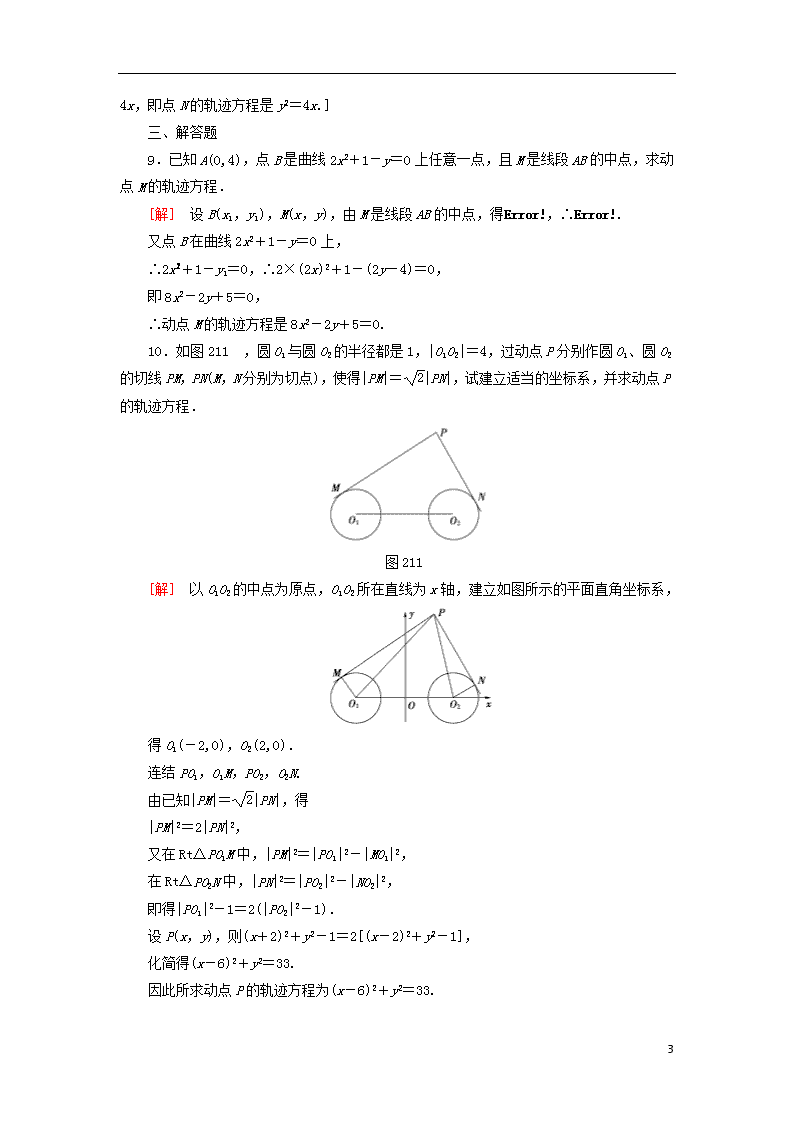‎ ‎【导学号：46342057】‎ y2＝4x　[由于||＝||，则P为MN的中点．设N(x，y)，则M(－x,0)，P，由·＝0，得·＝0，所以(－x)·1＋·＝0，则y2＝4x，即点N 5‎ 的轨迹方程是y2＝4x.]‎ 三、解答题 ‎9．已知A(0,4)，点B是曲线2x2＋1－y＝0上任意一点，且M是线段AB的中点，求动点M的轨迹方程．‎ ‎[解]　设B(x1，y1)，M(x，y)，由M是线段AB的中点，得，∴.‎ 又点B在曲线2x2＋1－y＝0上，‎ ‎∴2x＋1－y1＝0，∴2×(2x)2＋1－(2y－4)＝0，‎ 即8x2－2y＋5＝0，‎ ‎∴动点M的轨迹方程是8x2－2y＋5＝0.‎ ‎10．如图211，圆O1与圆O2的半径都是1，|O1O2|＝4，过动点P分别作圆O1、圆O2的切线PM，PN(M，N分别为切点)，使得|PM|＝|PN|，试建立适当的坐标系，并求动点P的轨迹方程．‎ 图211‎ ‎[解]　以O1O2的中点为原点，O1O2所在直线为x轴，建立如图所示的平面直角坐标系，‎ 得O1(－2,0)，O2(2,0)．‎ 连结PO1，O‎1M，PO2，O2N.‎ 由已知|PM|＝|PN|，得 ‎|PM|2＝2|PN|2，‎ 又在Rt△PO‎1M中，|PM|2＝|PO1|2－|MO1|2，‎ 在Rt△PO2N中，|PN|2＝|PO2|2－|NO2|2，‎ 即得|PO1|2－1＝2(|PO2|2－1)．‎ 设P(x，y)，则(x＋2)2＋y2－1＝2[(x－2)2＋y2－1]，‎ 化简得(x－6)2＋y2＝33.‎ 因此所求动点P的轨迹方程为(x－6)2＋y2＝33.‎ 5‎ ‎[能力提升练]‎ ‎1．方程x(x2＋y2－1)＝0和x2＋(x2＋y2－1)2＝0所表示的图形是(　　)‎ A．前后两者都是一条直线和一个圆 B．前后两者都是两个点 C．前者是一条直线和一个圆，后者是两个点 D．前者是两点，后者是一条直线和一个圆 C　[x(x2＋y2－1)＝0⇔x＝0或x2＋y2＝1，表示直线x＝0和圆x2＋y2＝1.x2＋(x2＋y2－1)2＝0⇔⇔表示点(0,1)，(0，－1)．]‎ ‎2．设过点P(x，y)的直线分别与x轴的正半轴和y轴的正半轴交于A，B两点，点Q与点P关于y轴对称，O为坐标原点．若＝2，且·＝1，则点P的轨迹方程是(　　) ‎ ‎【导学号：46342058】‎ A．x2＋3y2＝1(x>0，y>0)‎ B．x2－3y2＝1(x>0，y>0)‎ C．3x2－y2＝1(x>0，y>0)‎ D．3x2＋y2＝1(x>0，y>0)‎ A　[设A(a,0)，B(0，b)，a>0，b>0.由＝2，得(x，y－b)＝2(a－x，－y)，即a＝x>0，b＝3y>0.点Q(－x，y)，故由·＝1，得(－x，y)·(－a，b)＝1，即ax＋by＝1.将a，b代入ax＋by＝1，得所求的轨迹方程为x2＋3y2＝1(x>0，y>0)．]‎ ‎3．已知定长为6的线段，其端点A、B分别在x轴、y轴上移动，线段AB的中点为M，则点M的轨迹方程为________．‎ x2＋y2＝9　[作出图象如图所示，根据直角三角形的性质可知 ‎|OM|＝|AB|＝3.‎ 所以M的轨迹是以原点O为圆心，以3为半径的圆，‎ 故点M的轨迹方程为x2＋y2＝9.]‎ ‎4．已知两定点A(－2,0)，B(1,0)，如果动点P满足|PA|＝2|PB|，则点P的轨迹所包围的图形的面积等于________．‎ ‎4π　[设动点P(x，y)，‎ 依题意|PA|＝2|PB|，‎ 5‎ ‎∴＝2，‎ 化简得(x－2)2＋y2＝4，‎ 方程表示半径为2的圆，‎ 因此图形的面积S＝π·22＝4π.]‎ ‎5．过点P(2,4)作两条互相垂直的直线l1、l2，若l1交x轴于A点，l2交y轴于B点，求线段AB的中点M的轨迹方程. ‎ ‎【导学号：46342059】‎ ‎[解]　法一：如图，设点M的坐标为(x，y)，‎ ‎∵M为线段AB的中点，‎ ‎∴A点的坐标为(2x,0)，B点的坐标为(0,2y)．‎ ‎∵l1⊥l2，且l1，l2过点P(2,4)，‎ ‎∴PA⊥PB，即kPA·kPB＝－1，‎ 而kPA＝＝(x≠1)，‎ kPB＝＝，‎ ‎∴·＝－1(x≠1)，‎ 整理得x＋2y－5＝0(x≠1)．‎ ‎∵当x＝1时，A，B的坐标分别为(2,0)，(0,4)，‎ ‎∴线段AB的中点坐标是(1,2)，它满足方程x＋2y－5＝0.‎ 综上所述，点M的轨迹方程是x＋2y－5＝0.‎ 法二：设点M的坐标为(x，y)，则A，B两点的坐标分别是(2x,0)，(0,2y)，连接PM(如图)．‎ ‎∵l1⊥l2，∴2|PM|＝|AB|.‎ 而|PM|＝，‎ ‎|AB|＝，‎ ‎∴2＝，‎ 化简得x＋2y－5＝0，即为所求的点M的轨迹方程．‎ 5‎