江苏省南京市、盐城市2020届高三第一次模拟考试（1月） 数学（理） 13页

南京市、盐城市2020届高三年级第一次模拟考试 数 学 理 试 题 ‎ (总分160分，考试时间120分钟)‎ 注意事项：‎ ‎　　1．本试卷考试时间为120分钟，试卷满分160分，考试形式闭卷．‎ ‎　　2．本试卷中所有试题必须作答在答题卡上规定的位置，否则不给分．‎ ‎　　3．答题前，务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上．‎ 参考公式：‎ 柱体体积公式：，锥体体积公式：，其中为底面积，为高.‎ 样本数据的方差，其中.‎ 一、填空题（本大题共14小题，每小题5分，计70分. 不需写出解答过程，请把答案写在答题纸的指定位置上）‎ ‎1．已知集合，全集，则ðUA= ▲ ．‎ ‎(第5题图)‎ ‎2．设复数，其中为虚数单位，则 ▲ ．‎ ‎3．学校准备从甲、乙、丙三位学生中随机选两位学生参加问卷调查，则甲被选中的概率为 ▲ ．‎ ‎4．命题“，”的否定是 ▲ 命题.(填“真”或“假”)‎ ‎5．运行如图所示的伪代码，则输出的的值为 ▲ ．‎ ‎6．已知样本的平均数是，且，则此样本的方差是 ▲ ．‎ ‎7．在平面直角坐标系中，若抛物线上的点到其焦点的距离为，则点到点的距离为 ▲ ．‎ ‎8．若数列是公差不为0的等差数列，、、成等差数列，则的值为 ▲ ．‎ ‎9．在三棱柱中，点是棱上一点，记三棱柱与四棱锥 ‎·13·‎ 的体积分别为与，则 ▲ ．‎ ‎10．设函数（）的图象与轴交点的纵坐标为， 轴右侧第一个最低点的横坐标为，则的值为 ▲ ．‎ ‎11．已知是△的垂心（三角形三条高所在直线的交点），， 则的值为 ▲ .‎ ‎12．若无穷数列是等差数列，则其前10项的和为 ▲ ．‎ ‎13．已知集合，集合， 若，则的最小值为 ▲ ．‎ ‎14．若对任意实数，都有成立，则实数的值为 ▲ .‎ 二、解答题（本大题共6小题，计90分.解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内）‎ ‎15．(本小题满分14分)‎ ‎ 已知满足．‎ ‎（1）若，，求；‎ ‎（2）若，且，求．‎ ‎16．(本小题满分14分)‎ 如图，长方体中，已知底面是正方形，点是侧棱上的一点．‎ ‎（1）若//平面，求的值；‎ ‎（2）求证：．‎ ‎(第16题图) ‎ ‎·13·‎ ‎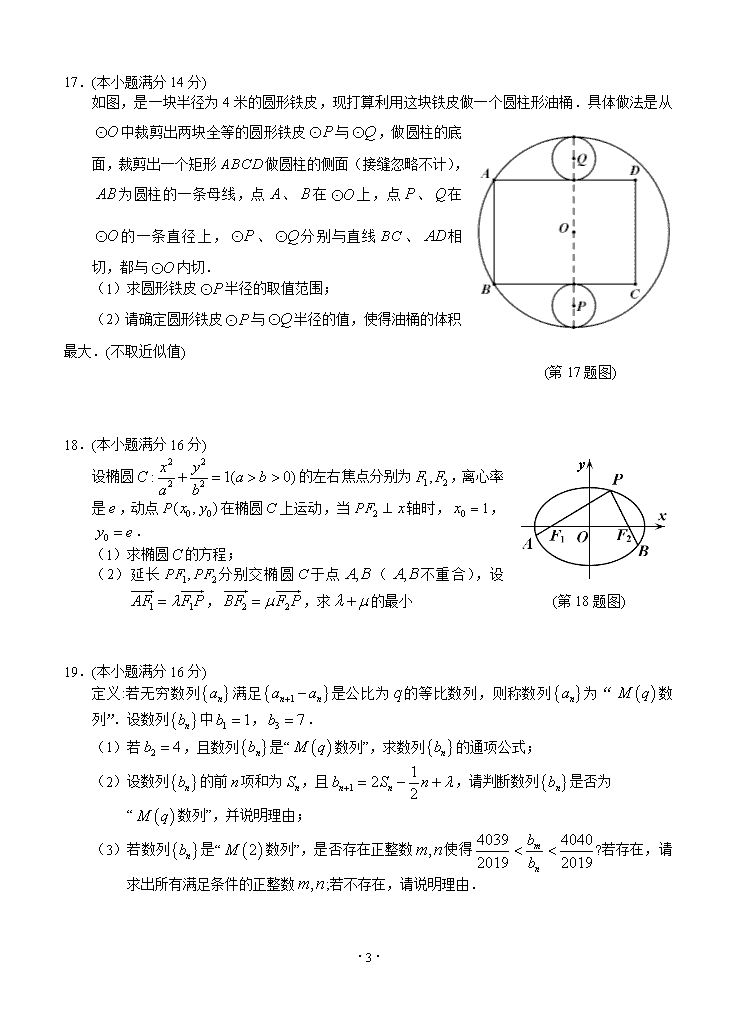17．(本小题满分14分)‎ 如图，是一块半径为4米的圆形铁皮，现打算利用这块铁皮做一个圆柱形油桶．具体做法是从中裁剪出两块全等的圆形铁皮与，做圆柱的底面，裁剪出一个矩形做圆柱的侧面（接缝忽略不计），为圆柱的一条母线，点、在上，点、在的一条直径上，、分别与直线、相切，都与内切．‎ ‎（1）求圆形铁皮半径的取值范围；‎ （2） 请确定圆形铁皮与半径的值，使得油桶的体积最大．(不取近似值)‎ ‎(第17题图) ‎ y ‎18．(本小题满分16分)‎ 设椭圆的左右焦点分别为，离心率是，动点在椭圆上运动，当轴时，，．‎ ‎（1）求椭圆的方程；‎ ‎（2）延长分别交椭圆于点（不重合），设，，求的最小 (第18题图)‎ ‎19．(本小题满分16分)‎ 定义:若无穷数列满足是公比为的等比数列，则称数列为“数列”．设数列中，．‎ ‎（1）若，且数列是“数列”，求数列的通项公式；‎ ‎（2）设数列的前项和为，且，请判断数列是否为 “数列”，并说明理由；‎ ‎（3）若数列是“数列”，是否存在正整数使得?若存在，请求出所有满足条件的正整数;若不存在，请说明理由．‎ ‎·13·‎ ‎20．(本小题满分16分)‎ 若函数为奇函数，且时有极小值．‎ ‎（1）求实数的值；‎ ‎（2）求实数的取值范围；‎ ‎（3）若恒成立，求实数的取值范围．‎ 南京市、盐城市2020届高三年级第一次模拟考试 数学附加题部分 ‎（本部分满分40分，考试时间30分钟）‎ ‎21．[选做题]（在A、B、C三个小题中只能选做2题，每小题10分，计20分．请把答案写在答题纸的指定区域内）‎ A.（选修4-2：矩阵与变换）‎ 已知圆经矩阵变换后得到圆，求实数的值.‎ B．（选修4-4：坐标系与参数方程）‎ 在极坐标系中，直线被曲线截得的弦为，当是最长弦时，求实数的值.‎ C．(选修4-5：不等式选讲）‎ 已知正实数满足，求的最小值.‎ ‎ ‎ ‎·13·‎ ‎[必做题]（第22、23题，每小题10分，计20分．请把答案写在答题纸的指定区域内）‎ ‎22．（本小题满分10分）‎ 如图，、是圆柱的两条母线， 、分别经过上下底面圆的圆心、，是下底面与垂直的直径，.‎ ‎（1）若，求异面直线与所成角的余弦值；‎ ‎（2）若二面角的大小为，求母线的长.‎ ‎23．（本小题满分10分）‎ 设()，记.‎ ‎（1）求；‎ ‎（2）记，求证：恒成立.‎ ‎·13·‎ 南京市、盐城市2020届高三年级第一次模拟考试 数学参考答案 一、填空题：本大题共14小题，每小题5分，计70分.‎ ‎1． 2． 3． 4．真 5． 6． 7．‎ ‎8． 9． 10． 11． 12．10 13． 14． 二、解答题：本大题共6小题，计90分.解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内.‎ ‎15．解：（1）由可知，‎ 移项可得，又，故， ………………………………………2分 又由，可知， ………………………4分 故在中，由正弦定理可得 ，所以. …………7分 ‎（2）由（1）知，所以时，，‎ 由即可得 ， ……………10分 ‎∴.…14分 ‎16．（1）证明：连结交于点，连结， ‎ 又因为平面，平面 平面平面，所以 ……………3分 因为四边形是正方形，对角线交于点 ，‎ 所以点是的中点，所以，‎ 所以在中，. ……………6分 ‎（2）证明：连结.‎ 因为为直四棱柱，所以侧棱垂直于底面，‎ 又平面，所以．…………………………………………………………8分 因为底面是正方形，所以． ……………………………………………10分 ‎·13·‎ 又，面， 面，‎ 所以面. ……………………………………………………………………………12分 又因为,所以，又因为，‎ 所以A1PÌ面ACC1A1,所以． ………………………………………14分 ‎17．解：（1）设半径为，则，‎ 所以的周长， ………………………………………4分 解得 ，故半径的取值范围为. …………………………………6分 ‎（2）在（1）的条件下，油桶的体积， ……………………………8分 设函数，‎ 所以，由于 ，‎ 所以在定义域上恒成立，‎ 故在定义域上单调递增，‎ 即当时，体积取到最大值. ………………………………………13分 答：半径的取值范围为，当时，体积取到最大值. ………………14分 ‎18.解：（1）由当轴时，可知， …………………………………………2分 将，代入椭圆方程得（※），‎ 而，，代入（※）式得，‎ 解得，故，∴椭圆的方程为.…………………………………………4分 ‎（2）方法一：设，由得，故，‎ 代入椭圆的方程得（＃）， ………………………………………8分 又由得，代入（＃）式得，‎ 化简得，即，显然，‎ ‎∴，故.……………………………………………………………12分 ‎·13·‎ 同理可得，故，‎ 当且仅当时取等号，故的最小值为. ………………………………………16分 方法二：由点，不重合可知直线与轴不重合，故可设直线的方程为，‎ 联立，消去得（☆），‎ 设，则与为方程（☆）的两个实根，‎ 由求根公式可得，故，则，……………8分 将点代入椭圆的方程得，‎ 代入直线的方程得，∴，‎ 由得，故 ‎.…………………………………………12分 同理可得，故，‎ 当且仅当时取等号，故的最小值为. ………………………………………16分 注：（1）也可设得，其余同理.‎ ‎（2）也可由运用基本不等式求解的最小值. ‎ ‎19．解：（1）∵，且数列是“数列”，‎ ‎∴，∴，∴，………………………2分 故数列是等差数列，公差为，‎ 故通项公式为，即. ………………………………………4分 ‎（2）由得，，故.‎ ‎·13·‎ 方法一：由得，‎ 两式作差得，即，‎ 又，∴，∴对恒成立，……………………6分 则，而，∴，∴，‎ ‎∴是等比数列， ………………………………………………………………………………8分 ‎∴，∴，∴，‎ ‎∴是公比为的等比数列，故数列是“数列”.………………………………10分 方法二：同方法一得对恒成立，‎ 则，两式作差得，而，‎ ‎∴，∴，以下同方法一. ……………………………10分 ‎（3）由数列是“数列”得，‎ 又，∴，∴，∴，∴，‎ ‎∴当时，‎ ‎，‎ 当时上式也成立，故， ……………………………12分 假设存在正整数使得，则，‎ 由可知，∴，又为正整数，∴，‎ 又，‎ ‎·13·‎ ‎∴，∴，∴，∴，‎ ‎∴，∴，∴，‎ 故存在满足条件的正整数，，. …………………………16分 ‎20．解：（1）由函数为奇函数，得在定义域上恒成立，‎ 所以 ，‎ 化简可得 ，所以. ……………………………………3分 ‎（2）法一：由（1）可得，‎ 所以，‎ 其中当时，由于恒成立，‎ 即恒成立，故不存在极小值. ………………………………………5分 当时，方程有两个不等的正根，‎ 故可知函数在上单调递增，‎ 在上单调递减，即在处取到极小值，‎ 所以，的取值范围是. ………………………………………9分 法二：由（1）可得，‎ 令，‎ 则，‎ 故当时，；当时，， …………………………………5分 故在上递减，在上递增，‎ ‎∴，‎ 若，则恒成立，单调递增，无极值点；‎ 所以，解得，‎ 取，则，‎ 又函数的图象在区间上连续不间断，故由函数零点存在性定理知在区间上，存在为函数的零点，为极小值.‎ 所以，的取值范围是. ………………………………………9分 ‎（3）由满足，‎ 代入， ‎ 消去m可得， ……………………………11分 构造函数，‎ 所以，当时， ，‎ ‎·13·‎ 所以当时，恒成立，故h(x)在[0，+)上为单调减函数，其中， 13分 则可转化为，‎ 故，由，设，‎ 可得当时，，在上递增，故，‎ 综上，的取值范围是 . ………………………………………16分 附加题答案 ‎21.（A）解：设圆上一点，经矩阵变换后得到圆上一点，‎ 所以，所以，………………………………………………5分 又圆，所以圆的方程为，‎ 化简得，‎ 所以，解得. ………………………………………………10分 ‎21.（B）解：以极点为原点，极轴为x轴的正半轴（单位长度相同）建立平面直角坐标系，‎ 由直线，可得直角坐标方程为，‎ 又曲线，所以，其直角坐标方程为， ………………5分 所以曲线是以为圆心，为半径的圆，‎ 为使直线被曲线（圆）截得的弦最长，所以直线过圆心，‎ 于是，解得. ……………………………………………………10分 ‎21.（C）解：因，所以，‎ 由柯西不等式得，‎ 即， …………………………………………………………………………………5分 当且仅当，即时取等号，解得，‎ ‎·13·‎ 所以当且仅当时，取最小值36. ……………………………………10分 ‎22．解：（1）以，，所在直线建立如图所示空间直角坐标系，‎ 由，，所以，，，，，，从而，，‎ 所以，‎ 所以异面直线与所成角的余弦值为. …………………………………4分 ‎（2）设，则，，‎ 所以，，，‎ 设平面的一个法向量，‎ 所以，‎ 所以，令，则，‎ 所以平面的一个法向量，‎ 同理可得平面的一个法向量，‎ 因为二面角的大小为，所以，‎ 解得或，‎ 由图形可知当二面角的大小为时, . …………………………10分 注：用传统方法也可，请参照评分.‎ ‎23．解：（1）令得，‎ 令得，‎ ‎·13·‎ 两式相加得，∴.…………………………3分 ‎（2）‎ ‎…………………………………………………………………………7分 要证，即证，只需证明，即证，‎ 当时，显然成立；‎ 当时，，即，‎ ‎∴对恒成立.‎ 综上，恒成立.……………………………………………………………………………10分 注：用数学归纳法或数列的单调性也可证明恒成立，请参照评分.‎ ‎·13·‎