2020版高中数学 第一章 解三角形第2课时 角度问题 5页

第2课时　角度问题 课后篇巩固探究 ‎　　　　　　　　　　　　　　　　　‎ ‎1.在静水中划船的速度是‎40 m/min,水流的速度是‎20 m/min,如果船从岸边A处出发,沿着与水流垂直的航线到达对岸,那么船的前进方向应指向河流的上游,且与河岸垂直方向所成的角为(　　)‎ A.15° B.30° C.45° D.60°‎ 解析如图所示,‎ ‎∵sin∠CAB=,∴∠CAB=30°.‎ 答案B ‎2.(2017·江西南昌二中月考)如图所示,在坡度一定的山坡A处测得山顶上一建筑物CD的顶端C相对于山坡的斜度为15°,向山顶前进‎100 m到达B处,又测得C相对于山坡的斜度为45°,若CD=‎50 m,山坡的坡角为θ,则cos θ=(　　)‎ A. 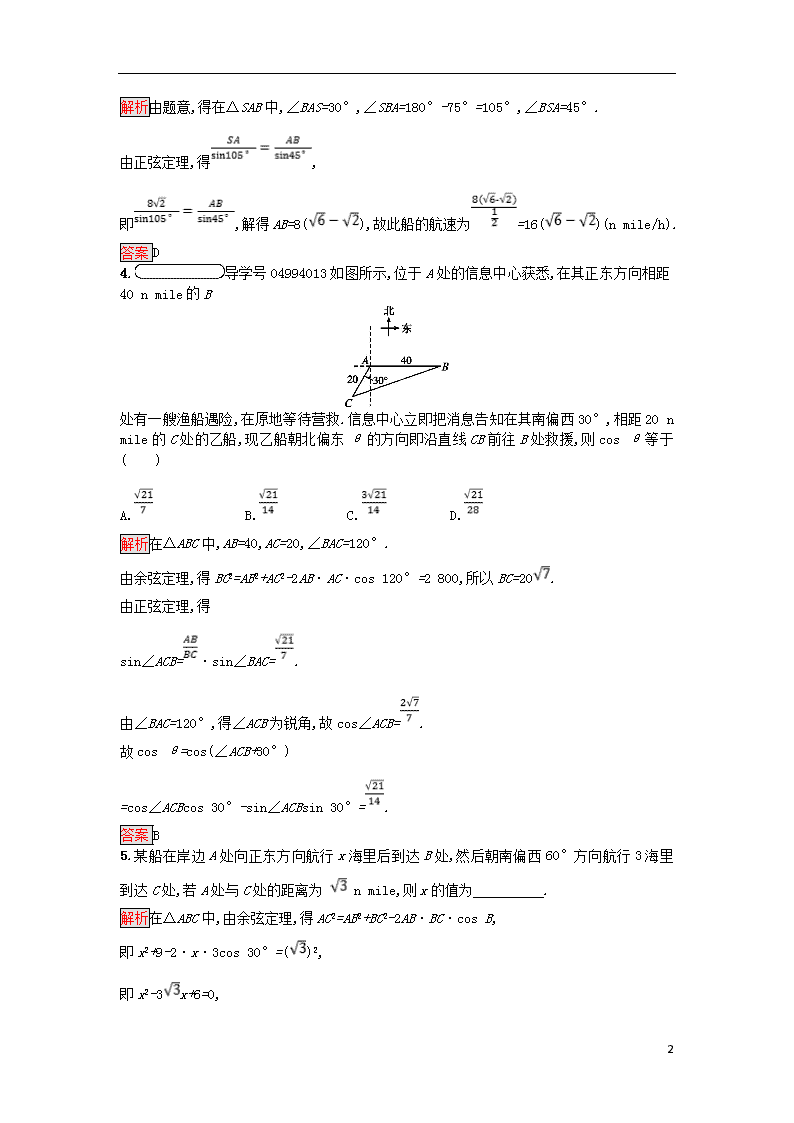B.‎-1 ‎C.2- D.‎ 解析在△ABC中,由正弦定理,得 BC==50()(m).在△BCD中,由正弦定理,得sin∠BDC=-1.由题图知cos θ=sin∠ADE=sin∠BDC=-1,故选B.‎ 答案B ‎3.一艘船上午9:30在A处,测得灯塔S在它的北偏东30°的方向,且与它相距8 n mile, 之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°的方向,则此船的航速是(　　)‎ A.8()n mile/h B.8()n mile/h C.16()n mile/h D.16()n mile/h 5‎ 解析由题意,得在△SAB中,∠BAS=30°,∠SBA=180°-75°=105°,∠BSA=45°.‎ 由正弦定理,得,‎ 即,解得AB=8(),故此船的航速为=16()(n mile/h).‎ 答案D ‎4.导学号04994013如图所示,位于A处的信息中心获悉,在其正东方向相距40 n mile的B 处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°,相距20 n mile的C处的乙船,现乙船朝北偏东θ的方向即沿直线CB前往B处救援,则cos θ等于(　　)‎ A. B. C. D.‎ 解析在△ABC中,AB=40,AC=20,∠BAC=120°.‎ 由余弦定理,得BC2=AB2+AC2-2AB·AC·cos 120°=2 800,所以BC=20.‎ 由正弦定理,得 sin∠ACB=·sin∠BAC=.‎ 由∠BAC=120°,得∠ACB为锐角,故cos∠ACB=.‎ 故cos θ=cos(∠ACB+30°)‎ ‎=cos∠ACBcos 30°-sin∠ACBsin 30°=.‎ 答案B ‎5.某船在岸边A处向正东方向航行x海里后到达B处,然后朝南偏西60°方向航行3海里到达C处,若A处与C处的距离为 n mile,则x的值为　　　　　. ‎ 解析在△ABC中,由余弦定理,得AC2=AB2+BC2-2AB·BC·cos B,‎ 即x2+9-2·x·3cos 30°=()2,‎ 即x2-3x+6=0,‎ 5‎ 解得x=2或x=.‎ 答案或2‎ ‎6.已知甲船在岛B的正南方A处,AB=10 n mile,甲船以4 n mile/h的速度向正北方向的岛B航行,同时乙船自岛B出发以6 n mile/h的速度向北偏东60°的方向航行,当甲、乙两船距离最近时,它们所航行的时间是　　　h. ‎ 解析如图,设甲、乙两船距离最近时航行时间为t h,距离为s n mile,此时甲船到达C处,则甲船距离B岛(10-4t)n mile,乙船距离B岛6t n mile,所以由余弦定理,得cos 120°==-,化简,得s2=28t2-20t+100,所以当t=时,s2取最小值,即当甲、乙两船距离最近时,它们所航行的时间是 h.‎ 答案 ‎7.某人见一建筑物A在正北方向,另一建筑物B在北偏西30°方向.此人沿北偏西70°方向行走了‎3 km后到达C,则见A在其北偏东56°方向上,B在其北偏东74°方向上,试求这两个建筑物间的距离.‎ 解如图,在△BCO中,∠BOC=70°-30°=40°,∠BCO=(180°-70°)-74°=36°,‎ ‎∴∠CBO=180°-40°-36°=104°.‎ ‎∵OC=3,由正弦定理,得,‎ 则BO=.在△ACO中,∠AOC=70°,∠CAO=56°,则∠ACO=54°.由正弦定理,得,则AO=.在△ABO中,由余弦定理,得AB=‎ 5‎ ‎≈1.630(km)=1 630(m).‎ 故这两个建筑物间的距离约为1 ‎630 m.‎ ‎8.平面内三个力F1,F2,F3作用于同一点,且处于平衡状态.已知F1,F2的大小分别为1 N, N,F1与F2的夹角为45°,求F3的大小及F3与F1的夹角的大小.‎ 解 如图,设F1与F2的合力为F,则F3=-F.‎ ‎∵∠BOC=45°,‎ ‎∴∠ABO=135°.‎ 在△OBA中,由余弦定理,得|F|2=|F1|2+|F2|2-2|F1|·|F2|cos 135°=12+-2×1×cos 135°=4+2.‎ ‎∴|F|=1+,‎ 即|F3|=+1.‎ 又由正弦定理,得 sin∠BOA=.‎ ‎∴∠BOA=30°.‎ ‎∴∠BOD=150°.‎ 故F3的大小为(+1)N,F1与F3的夹角为150°.‎ ‎9.导学号04994014某海上养殖基地A,接到气象部门预报,位于基地南偏东60°方向相距20(+1)n mile的海面上有一台风中心,影响半径为20 n mile,正以10 n mile/h的速度沿某一方向匀速直线前进,预计台风中心将从基地东北方向刮过且(+1)h后开始影响基地持续2 h.求台风移动的方向.‎ 解如图,设预报时台风中心为B,开始影响基地时台风中心为C 5‎ ‎,基地刚好不受影响时台风中心为D,则B,C,D在一条直线上,且AD=20 n mile,AC=20 n mile.‎ 由题意,得AB=20(+1)n mile,DC=20 n mile,BC=10+1)n mile.‎ 在△ADC中,‎ ‎∵DC2=AD2+AC2,‎ ‎∴∠DAC=90°,∠ADC=45°.‎ 在△ABC中,‎ 由余弦定理,得 cos∠BAC=.‎ ‎∴∠BAC=30°.‎ ‎∵B位于A的南偏东60°方向,且60°+30°+90°=180°,∴D位于A的正北方向.‎ 又∠ADC=45°,∴台风移动的方向为向量的方向,即北偏西45°方向.‎ 5‎