高考数学专题复习练习：单元质检十一 6页

单元质检十一　概率 ‎(时间:45分钟　满分:100分)‎ ‎　单元质检卷第25页　 ‎ 一、选择题(本大题共6小题,每小题7分,共42分)‎ ‎1.口袋中有100个大小相同的红球、白球、黑球,其中红球45个,从口袋中摸出一个球,摸出白球的概率为0.23,则摸出黑球的概率为(　　)‎ ‎　　　　　　　　　　　　　　　　　　　‎ A.0.45 B.0.67 C.0.64 D.0.32‎ 答案D 解析摸出红球的概率为0.45,摸出白球的概率为0.23,故摸出黑球的概率为1-0.45-0.23=0.32.‎ ‎2.(2016山西运城期末)若m∈(4,7),则直线y=kx+k与圆x2+y2+mx+4=0至少有一个交点的概率是(　　)‎ A.‎1‎‎5‎ B.‎2‎‎3‎ C.‎3‎‎5‎ D.‎1‎‎3‎〚导学号74920408〛‎ 答案B 解析∵y=kx+k,∴y=k(x+1),‎ ‎∴直线y=kx+k恒过定点M(-1,0).‎ ‎∵直线y=kx+k与圆x2+y2+mx+4=0至少有一个交点,∴点M在圆内或圆上,‎ ‎∴(-1)2+0-m+4≤0,解得m≥5.①‎ ‎∵x2+y2+mx+4=0表示圆,∴m2+0-16>0,解得m>4或m<-4.②‎ 综合①②得m≥5,又m∈(4,7),可知m∈[5,7),故由几何概型可知所求概率为‎7-5‎‎7-4‎‎=‎‎2‎‎3‎.‎ ‎3.有三个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为(　　)‎ A.‎1‎‎3‎ B.‎1‎‎2‎ C.‎2‎‎3‎ D.‎‎3‎‎4‎ 答案A 解析记三个兴趣小组分别为1,2,3,甲参加兴趣小组1,2,3分别记为“甲1”“甲2”“甲3”,乙参加兴趣小组1,2,3分别记为“乙1”“乙2”“乙3”,则基本事件为“(甲1,乙1),(甲1,乙2),(甲1,乙3),(甲2,乙1),(甲2,乙2),(甲2,乙3),(甲3,乙1),(甲3,乙2),(甲3,乙3)”,共9个,记事件A为“甲、乙两位同学参加同一个兴趣小组”,其中事件A有“(甲1,乙1),(甲2,乙2),(甲3,乙3)”,共3个.因此P(A)=‎3‎‎9‎‎=‎‎1‎‎3‎.‎ ‎4.已知m∈{-2,-1,0,1,2,3},n∈{-3,-2,-1,0,1,2},且方程x‎2‎m‎+‎y‎2‎n=1有意义,则方程x‎2‎m‎+‎y‎2‎n=1可表示双曲线的概率为(　　)‎ A.‎36‎‎25‎ B.1 C.‎9‎‎25‎ D.‎13‎‎25‎〚导学号74920409〛‎ 答案D 解析由题设知m>0,‎n<0,‎或m<0,‎n>0,‎ 当m>0,‎n<0‎时,有不同取法3×3=9种.‎ 当m<0,‎n>0‎时,有不同取法2×2=4种.‎ 所以,所求概率为‎9+4‎‎5×5‎‎=‎‎13‎‎25‎.‎ ‎5.(2016福建福州质检)在2015年全国青运会火炬传递活动中,有编号分别为1,2,3,4,5的5名火炬手,若从中任选2名,则选出的火炬手的编号相邻的概率为(　　)‎ A.‎3‎‎10‎ B.‎5‎‎8‎ C.‎7‎‎10‎ D.‎2‎‎5‎〚导学号74920410〛‎ 答案D 解析基本事件总数为10,分别是{1,2},{1,3},{1,4},{1,5},{2,3},{2,4},{2,5},{3,4},{3,5},{4,5},其中选出的火炬手的编号相邻的有{1,2},{2,3},{3,4},{4,5},共4种,故选出的火炬手的编号相邻的概率为‎4‎‎10‎‎=‎‎2‎‎5‎.‎ ‎6.已知P是△ABC所在平面内一点,4PB+5PC+3PA=0,现将一粒红豆随机撒在△ABC内,则红豆落在△PBC内的概率是(　　)‎ A.‎1‎‎4‎ B.‎‎1‎‎3‎ C.‎5‎‎12‎ D.‎1‎‎2‎〚导学号74920411〛‎ 答案A 解析依题意,易知点P位于△ABC内,作PB‎1‎=4PB‎,‎PC‎1‎=5PC‎,‎PA‎1‎=3PA,则有PB‎1‎‎+PC‎1‎+‎PA‎1‎=0,点P是△A1B1C1的重心.S‎△PB‎1‎C‎1‎‎=S‎△PC‎1‎A‎1‎=‎S‎△PA‎1‎B‎1‎,而S△PBC=‎1‎‎4‎‎×‎‎1‎‎5‎S‎△PB‎1‎C‎1‎,S△PCA=‎1‎‎3‎‎×‎‎1‎‎5‎‎·‎S‎△PC‎1‎A‎1‎,S△PAB=‎1‎‎3‎‎×‎‎1‎‎4‎S‎△PA‎1‎B‎1‎,因此S△PBC∶S△PCA∶S△PAB=3∶4∶5,‎ 即S‎△PBCS‎△PBC‎+S‎△PCA+‎S‎△PAB‎=‎3‎‎3+4+5‎=‎‎1‎‎4‎,即红豆落在△PBC内的概率等于‎1‎‎4‎,故选A.‎ 二、填空题(本大题共2小题,每小题7分,共14分)‎ ‎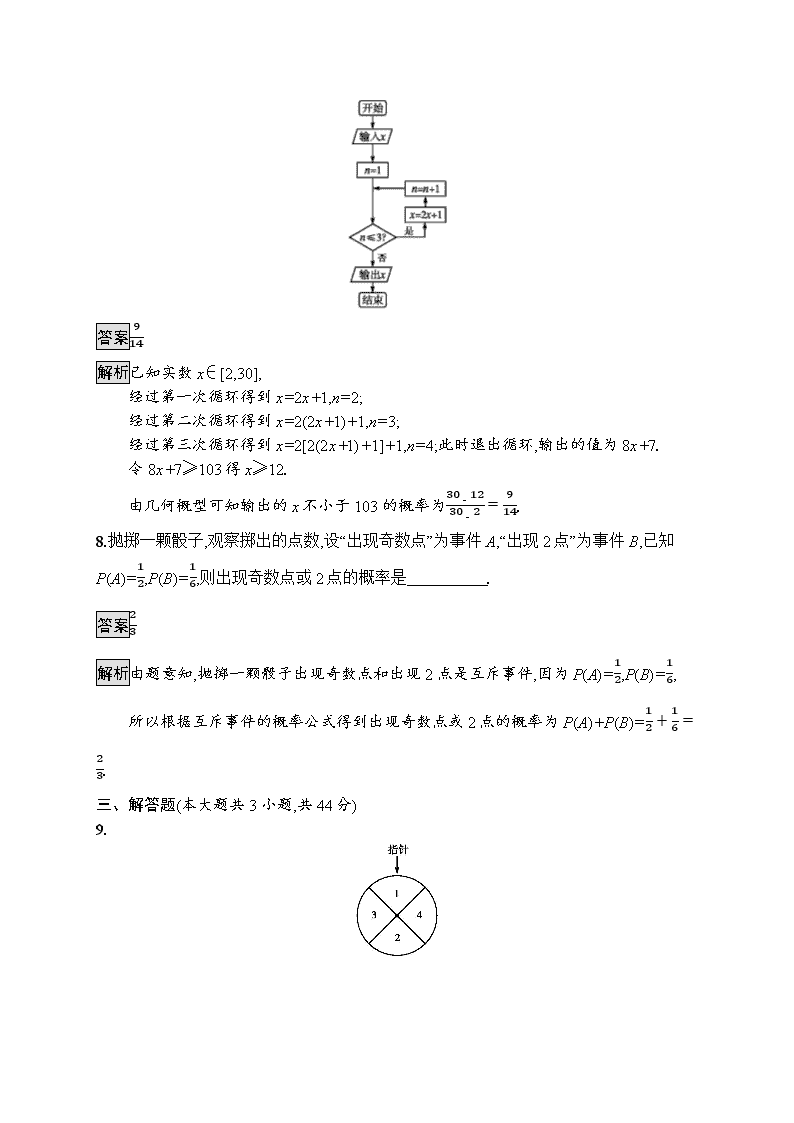7.(2016山东潍坊模拟)已知实数x∈[2,30],执行如图所示的程序框图,则输出的x不小于103的概率是　　　　　. ‎ 答案‎9‎‎14‎ 解析已知实数x∈[2,30],‎ 经过第一次循环得到x=2x+1,n=2;‎ 经过第二次循环得到x=2(2x+1)+1,n=3;‎ 经过第三次循环得到x=2[2(2x+1)+1]+1,n=4;此时退出循环,输出的值为8x+7.‎ 令8x+7≥103得x≥12.‎ 由几何概型可知输出的x不小于103的概率为‎30-12‎‎30-2‎‎=‎‎9‎‎14‎.‎ ‎8.抛掷一颗骰子,观察掷出的点数,设“出现奇数点”为事件A,“出现2点”为事件B,已知P(A)=‎1‎‎2‎,P(B)=‎1‎‎6‎,则出现奇数点或2点的概率是　　　　　. ‎ 答案‎2‎‎3‎ 解析由题意知,抛掷一颗骰子出现奇数点和出现2点是互斥事件,因为P(A)=‎1‎‎2‎,P(B)=‎1‎‎6‎,‎ 所以根据互斥事件的概率公式得到出现奇数点或2点的概率为P(A)+P(B)=‎1‎‎2‎‎+‎1‎‎6‎=‎‎2‎‎3‎.‎ 三、解答题(本大题共3小题,共44分)‎ ‎9.‎ ‎(14分)(2016山东,文16)某儿童乐园在“六一”儿童节推出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:‎ ‎①若xy≤3,则奖励玩具一个;‎ ‎②若xy≥8,则奖励水杯一个;‎ ‎③其余情况奖励饮料一瓶.‎ 假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.‎ ‎(1)求小亮获得玩具的概率;‎ ‎(2)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.‎ 解用数对(x,y)表示儿童参加活动先后记录的数,则基本事件空间Ω与点集S={(x,y)|x∈N,y∈N,1≤x≤4,1≤y≤4}一一对应.‎ 因为S中元素的个数是4×4=16,‎ 所以基本事件总数n=16.‎ ‎(1)记“xy≤3”为事件A,则事件A包含的基本事件数共5个,即(1,1),(1,2),(1,3),(2,1),(3,1).‎ 所以P(A)=‎5‎‎16‎,即小亮获得玩具的概率为‎5‎‎16‎.‎ ‎(2)记“xy≥8”为事件B,“3‎‎5‎‎16‎,‎ 所以小亮获得水杯的概率大于获得饮料的概率.〚导学号74920412〛‎ ‎10.(15分)某保险公司利用简单随机抽样的方法,对投保车辆进行抽样,样本车辆中每辆车的赔付结果统计如下:‎ 赔付金额(元)‎ ‎0‎ ‎1 000‎ ‎2 000‎ ‎3 000‎ ‎4 000‎ 车辆数(辆)‎ ‎500‎ ‎130‎ ‎100‎ ‎150‎ ‎120‎ ‎(1)若每辆车的投保金额均为2 800元,估计赔付金额大于投保金额的概率;‎ ‎(2)在样本车辆中,车主是新司机的占10%,在赔付金额为4 000元的样本车辆中,车主是新司机的占20%,估计在已投保车辆中,新司机获赔金额为4 000元的概率.‎ 解(1)设A表示事件“赔付金额为3 000元”,B表示事件“赔付金额为4 000元”,以频率估计概率得P(A)=‎150‎‎1 000‎=0.15,P(B)=‎120‎‎1 000‎=0.12.‎ 由于投保金额为2 800元,赔付金额大于投保金额对应的情形是3 000元和4 000元,所以其概率为P(A)+P(B)=0.15+0.12=0.27.‎ ‎(2)设C表示事件“投保车辆中新司机获赔4 000元”,由已知,样本车辆中车主为新司机的有0.1×1 000=100辆,而赔付金额为4 000元的车辆中,车主为新司机的有0.2×120=24辆.‎ 所以样本车辆中新司机车主获赔金额为4 000元的频率为‎24‎‎100‎=0.24,由频率估计概率得P(C)=0.24.〚导学号74920413〛‎ ‎11.(15分)(2016山东潍坊二模)济南天下第一泉风景区为了做好宣传工作,准备在A和B两所大学分别招募8名和12名志愿者,将这20名志愿者的身高编成的茎叶图(单位:cm)(叶中的数字都是按从小到大排列)如图所示.若身高在175 cm以上(包括175 cm)定义为“高精灵”,身高在175 cm以下(不包括175 cm)定义为“帅精灵”.已知A大学志愿者的身高的平均数为176 cm,B大学志愿者的身高的中位数为168 cm.‎ ‎(1)求x,y的值;‎ ‎(2)如果用分层抽样的方法从“高精灵”和“帅精灵”中抽取5人,再从这5人中选2人,求至少有一人为“高精灵”的概率.‎ 解(1)由题意可知,‎ ‎159+168+170+170+x+176+182+187+191‎‎8‎ ‎=176,‎ ‎160+y+169‎‎2‎‎=168,‎ 解得x=5,y=7.‎ ‎(2)由题意可得,“高精灵”有8人,“帅精灵”有12人,若从“高精灵”和“帅精灵”中抽取5人,则“高精灵”和“帅精灵”的人数分别为8×‎5‎‎20‎=2,12×‎5‎‎20‎=3.‎ 记抽取的“高精灵”分别为b1,b2,“帅精灵”为c1,c2,c3.‎ 从已经抽取的5人中任选2人的所有可能为(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3),(c1,c2),(c1,c3),(c2,c3)共10种结果;‎ 记“从这5人中选2人,至少有一人为‘高精灵’”为事件A,则事件A有(b1,b2),(b1,c1),(b1,c2),(b1,c3),(b2,c1),(b2,c2),(b2,c3)共7种结果,故P(A)=‎7‎‎10‎.〚导学号74920414〛‎