高考数学专题复习练习：单元质检十 7页

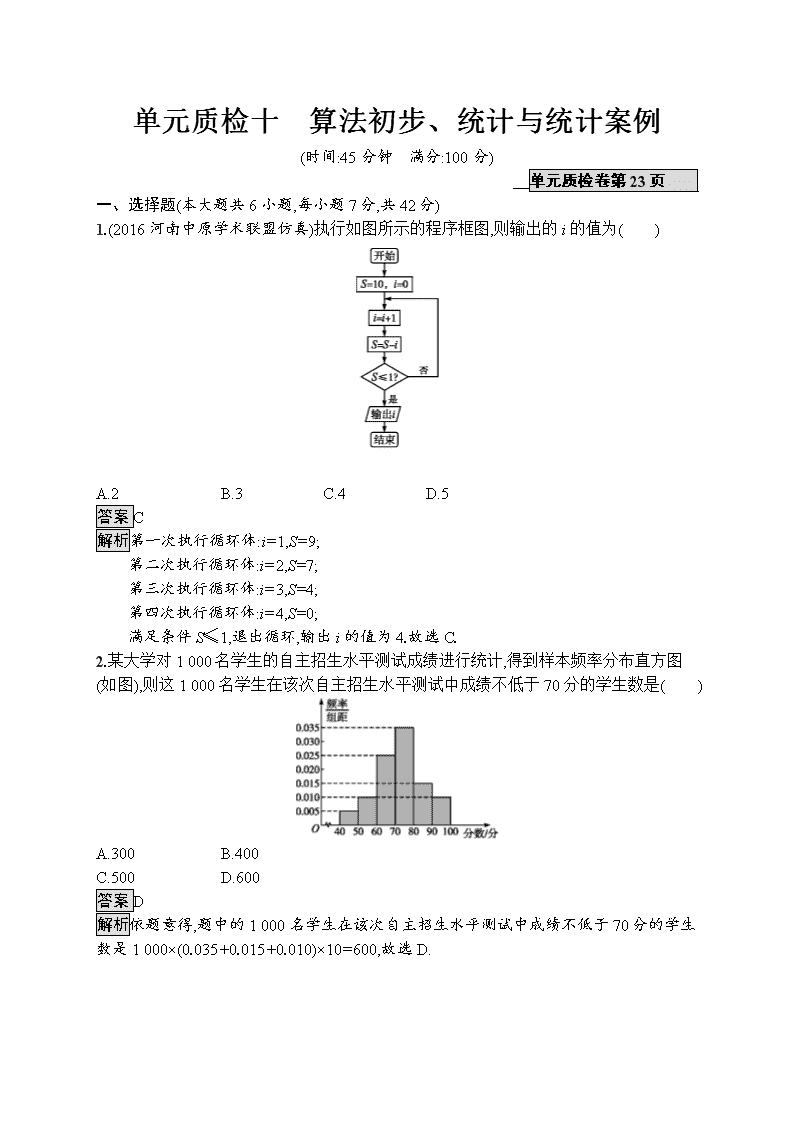
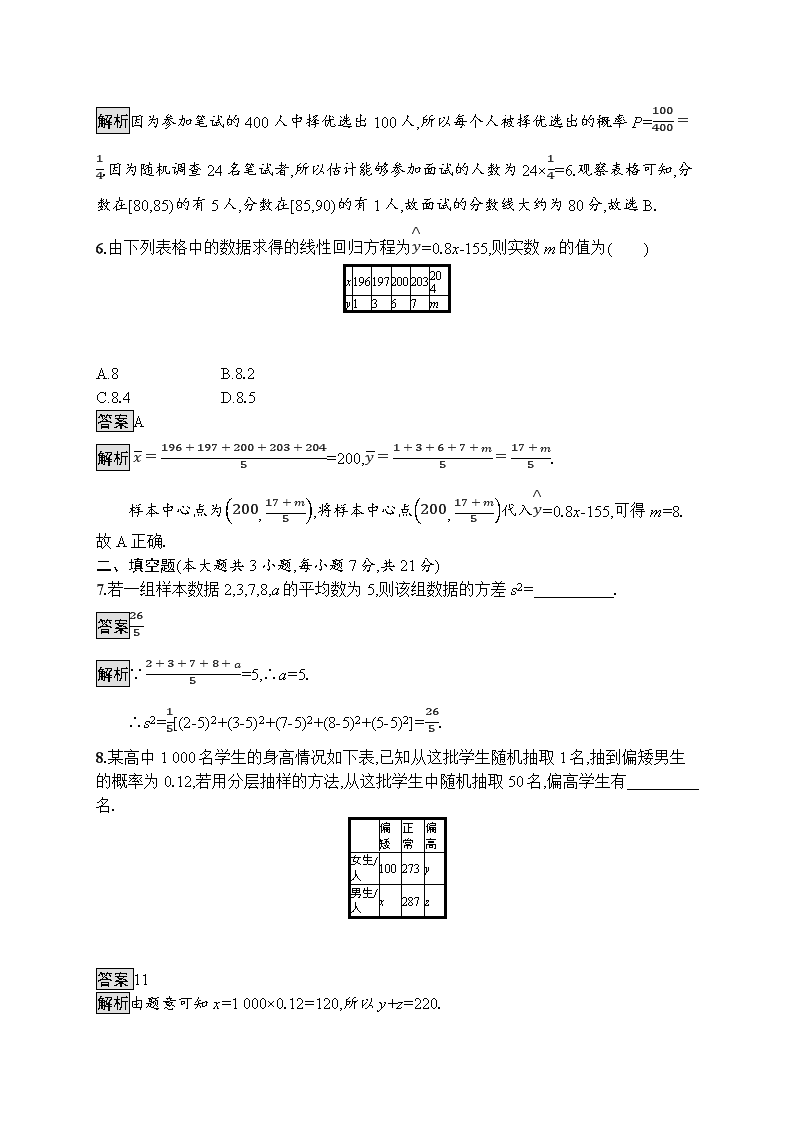
单元质检十　算法初步、统计与统计案例 ‎(时间:45分钟　满分:100分)‎ ‎　单元质检卷第23页　 ‎ 一、选择题(本大题共6小题,每小题7分,共42分)‎ ‎1.(2016河南中原学术联盟仿真)执行如图所示的程序框图,则输出的i的值为(　　)‎ ‎　　　　　　　　　　　　　　　　　　　‎ A.2 B.3 C.4 D.5‎ 答案C 解析第一次执行循环体:i=1,S=9;‎ 第二次执行循环体:i=2,S=7;‎ 第三次执行循环体:i=3,S=4;‎ 第四次执行循环体:i=4,S=0;‎ 满足条件S≤1,退出循环,输出i的值为4.故选C.‎ ‎2.某大学对1 000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这1 000名学生在该次自主招生水平测试中成绩不低于70分的学生数是(　　)‎ A.300 B.400‎ C.500 D.600‎ 答案D 解析依题意得,题中的1 000名学生在该次自主招生水平测试中成绩不低于70分的学生数是1 000×(0.035+0.015+0.010)×10=600,故选D.‎ ‎3.(2016安徽江淮十校5月模拟)某校共有2 000名学生,各年级男、女生人数如表所示.已知在全校学生中随机抽取1名,抽到二年级女生的概率是0.18.现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为(　　)‎ 一年级 二年级 三年级 女生 ‎363‎ x y 男生 ‎387‎ ‎390‎ z A.12 B.16 C.18 D.24‎ 答案B 解析由题意可得二年级的女生的人数为2 000×0.18=360,则一、二年级学生总数363+387+360+390=1 500,故三年级学生总数是2 000-1 500=500.‎ 因此,用分层抽样法在三年级抽取的学生数为64×‎500‎‎2 000‎=16.故选B.‎ ‎4.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.某地某日早7点到晚8点甲、乙两个PM2.5监测点统计的数据(单位:毫克/立方米)列出的茎叶图如图所示,则甲、乙两地PM2.5的方差较小的是(　　)‎ A.甲 B.乙 C.甲、乙相等 D.无法确定 答案A 解析从茎叶图上可以观察到:甲监测点的样本数据比乙监测点的样本数据更加集中,因此甲地PM2.5的方差较小.‎ ‎5.某高校进行自主招生,先从报名者中筛选出400人参加笔试,再按笔试成绩择优选出100人参加面试.现随机调查了24名笔试者的成绩,如下表所示:‎ 分数段 ‎[60,65)‎ ‎[65,70)‎ ‎[70,75)‎ ‎[75,80)‎ ‎[80,85)‎ ‎[85,90]‎ 人数 ‎2‎ ‎3‎ ‎4‎ ‎9‎ ‎5‎ ‎1‎ 据此估计允许参加面试的分数线是(　　)‎ A.75 B.80 C.85 D.90〚导学号74920406〛‎ 答案B 解析因为参加笔试的400人中择优选出100人,所以每个人被择优选出的概率P=‎100‎‎400‎‎=‎‎1‎‎4‎.因为随机调查24名笔试者,所以估计能够参加面试的人数为24×‎1‎‎4‎=6.观察表格可知,分数在[80,85)的有5人,分数在[85,90)的有1人,故面试的分数线大约为80分,故选B.‎ ‎6.由下列表格中的数据求得的线性回归方程为y‎^‎=0.8x-155,则实数m的值为(　　)‎ x ‎196‎ ‎197‎ ‎200‎ ‎203‎ ‎204‎ y ‎1‎ ‎3‎ ‎6‎ ‎7‎ m A.8 B.8.2‎ C.8.4 D.8.5‎ 答案A 解析 x‎=‎‎196+197+200+203+204‎‎5‎=200,y‎=‎1+3+6+7+m‎5‎=‎‎17+m‎5‎.‎ 样本中心点为‎200,‎‎17+m‎5‎,将样本中心点‎200,‎‎17+m‎5‎代入y‎^‎=0.8x-155,可得m=8.故A正确.‎ 二、填空题(本大题共3小题,每小题7分,共21分)‎ ‎7.若一组样本数据2,3,7,8,a的平均数为5,则该组数据的方差s2=　　　　　. ‎ 答案‎26‎‎5‎ 解析∵‎2+3+7+8+a‎5‎=5,∴a=5.‎ ‎∴s2=‎1‎‎5‎[(2-5)2+(3-5)2+(7-5)2+(8-5)2+(5-5)2]=‎26‎‎5‎.‎ ‎8.某高中1 000名学生的身高情况如下表,已知从这批学生随机抽取1名,抽到偏矮男生的概率为0.12,若用分层抽样的方法,从这批学生中随机抽取50名,偏高学生有　　　　　名. ‎ 偏矮 正常 偏高 女生/人 ‎100‎ ‎273‎ y 男生/人 x ‎287‎ z 答案11‎ 解析由题意可知x=1 000×0.12=120,所以y+z=220.‎ 所以偏高学生占学生总数的比例为‎220‎‎1 000‎‎=‎‎11‎‎50‎,所以随机抽取50名学生中偏高学生有50×‎11‎‎50‎=11(名).‎ ‎9.(2016河北唐山一模改编)执行如图所示的程序框图,输出S的值为　　　　　. ‎ 答案ln 4‎ 解析根据题意,模拟程序框图的运行过程,可得i=1,S=0;‎ 满足条件i<4,S=ln 2,i=2;‎ 满足条件i<4,S=ln 2+ln 3-ln 2=ln 3,i=3;‎ 满足条件i<4,S=ln 3+ln 4-ln 3=ln 4,i=4;‎ 不满足条件i<4,退出循环,输出S的值为ln 4.‎ 三、解答题(本大题共3小题,共37分)‎ ‎10.(12分)(2016内蒙古赤峰模拟)从某校随机抽取200名学生,获得了他们的一周课外阅读时间(单位:小时)的数据,整理得到数据的频数分布表和频数分布直方图(如图).‎ 编　号 分　组 频　数 ‎1‎ ‎[0,2)‎ ‎12‎ ‎2‎ ‎[2,4)‎ ‎16‎ ‎3‎ ‎[4,6)‎ ‎34‎ ‎4‎ ‎[6,8)‎ ‎44‎ ‎5‎ ‎[8,10)‎ ‎50‎ ‎6‎ ‎[10,12)‎ ‎24‎ ‎7‎ ‎[12,14)‎ ‎12‎ ‎8‎ ‎[14,16)‎ ‎4‎ ‎9‎ ‎[16,18)‎ ‎4‎ 合　　计 ‎200‎ ‎(1)从该校随机选取一名学生,试估计这名学生该周课外阅读时间少于12小时的概率;‎ ‎(2)求频率分布直方图中的a,b的值;‎ ‎(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的200名学生该周课外阅读时间的平均数在第几组.‎ 解(1)由频率分布表可知该周课外阅读时间不少于12小时的频数为12+4+4=20,故可估计该周课外阅读时间少于12小时的概率为1-‎20‎‎200‎=0.9.‎ ‎(2)由频率分布表可知数据在[4,6)的频数为34,故这一组的频率为0.17,即a=0.085,数据在[8,10)的频数为50,故这一组的频率为0.25,即b=0.125.‎ ‎(3)数据的平均数为‎1‎‎200‎(12×1+3×16+5×34+7×44+9×50+11×24+13×12+15×4+17×4)=7.68(小时),故样本中的200名学生该周课外阅读时间的平均数在第四组.〚导学号74920407〛‎ ‎11.(12分)随着我国经济的发展,居民的储蓄存款逐年增长.设某地区城乡居民人民币储蓄存款(年底余额)如下表:‎ 年　　份 ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ 时间代号t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 储蓄存款y/千亿元 ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎10‎ ‎(1)求y关于t的线性回归方程y‎^‎‎=‎b‎^‎t+a‎^‎;‎ ‎(2)用所求回归方程预测该地区2017年(t=6)的人民币储蓄存款.‎ 附:回归方程y‎^‎‎=‎b‎^‎t+a‎^‎中,b‎^‎‎=‎∑‎i=1‎ntiyi‎-nt ‎y‎∑‎i=1‎nti‎2‎‎-nt‎2‎,a‎^‎=y-‎b‎^‎t.‎ 解(1)列表计算如下:‎ i ti yi ti‎2‎ tiyi ‎1‎ ‎1‎ ‎5‎ ‎1‎ ‎5‎ ‎2‎ ‎2‎ ‎6‎ ‎4‎ ‎12‎ ‎3‎ ‎3‎ ‎7‎ ‎9‎ ‎21‎ ‎4‎ ‎4‎ ‎8‎ ‎16‎ ‎32‎ ‎5‎ ‎5‎ ‎10‎ ‎25‎ ‎50‎ ‎∑‎ ‎15‎ ‎36‎ ‎55‎ ‎120‎ 这里n=5,t‎=‎‎1‎n‎∑‎i=1‎nti=‎15‎‎5‎=3,y‎=‎‎1‎n‎∑‎i=1‎nyi=‎36‎‎5‎=7.2.‎ 又‎∑‎i=1‎nti‎2‎-nt‎2‎=55-5×32=10,‎∑‎i=1‎ntiyi-nt‎ ‎y=120-5×3×7.2=12,从而b‎^‎‎=‎∑‎i=1‎ntiyi‎-nt　‎y‎∑‎i=1‎nti‎2‎‎-nt‎2‎=‎‎12‎‎10‎=1.2,a‎^‎‎=y-‎b‎^‎t=7.2-1.2×3=3.6,故所求回归方程为y‎^‎=1.2t+3.6.‎ ‎(2)将t=6代入回归方程可预测该地区2017年的人民币储蓄存款为y‎^‎=1.2×6+3.6=10.8(千亿元).‎ ‎12.(13分)(2016山东泰安二模)某中学为研究学生的身体素质与课外体育锻炼时间的关系,对该校200名学生的课外体育锻炼平均每天运动的时间(单位:分钟)进行调查,将收集到的数据分成[0,10),[10,20),[20,30),[30,40),[40,50),[50,60]六组,并作出频率分布直方图(如图).将日均课外体育锻炼时间不低于40分钟的学生评价为“课外体育达标”.‎ ‎(1)请根据频率分布直方图中的数据填写下面的2×2列联表,并通过计算判断是否能在犯错误的概率不超过0.01的前提下认为“课外体育达标”与性别有关?‎ 课外体育不达标 课外体育达标 合计 男 ‎60‎ ‎　　　 ‎ ‎　 ‎ 女 ‎　　　 ‎ ‎　　　 ‎ ‎110‎ 合计 ‎　　　 ‎ ‎　　　 ‎ ‎　 ‎ ‎(2)现从“课外体育达标”学生中按分层抽样抽取5人,再从这5名学生中随机抽取2人参加体育知识问卷调查,求抽取的这2人课外体育锻炼时间都在[40,50)内的概率.‎ 附参考公式与数据:K2=‎n(ad-bc‎)‎‎2‎‎(a+b)(c+d)(a+c)(b+d)‎ P(K2≥k0)‎ ‎0.10‎ ‎0.05‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k0‎ ‎2.706‎ ‎3.841‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 解(1)根据频率分布直方图,得“课外体育达标”的学生数为200×(0.020+0.005)×10=50.‎ 又由2×2列联表可知“课外体育达标”的男生人数为30,女生人数为20.‎ 补全2×2列联表如下:‎ 课外体育不达标 课外体育达标 合计 男 ‎60‎ ‎30‎ ‎90‎ 女 ‎90‎ ‎20‎ ‎110‎ 合计 ‎150‎ ‎50‎ ‎200‎ 计算K2=n(ad-bc‎)‎‎2‎‎(a+b)(c+d)(a+c)(b+d)‎‎=‎‎200×(60×20-90×30‎‎)‎‎2‎‎90×110×150×50‎≈6.061<6.635,故在犯错误的概率不超过0.01的前提下不能认为“课外体育达标”与性别有关;‎ ‎(2)从“课外体育达标”学生中按分层抽样抽取5人,其中课外锻炼时间在[40,50)内有5×‎0.020‎‎0.020+0.005‎=4人,分别记为a,b,c,d;‎ 在[50,60]上有1人,记为E.‎ 从这5人中抽取2人,总的基本事件有ab,ac,ad,aE,bc,bd,bE,cd,cE,dE共10种,其中2人都在[40,50)内的基本事件有ab,ac,ad,bc,bd,cd共6种,故所求的概率为‎6‎‎10‎=0.6.‎