新课标高一数学同步测试4(必修2-14套) 6页

新课标高一数学同步测试（4）—1.2 点、线、面之间的位置关系 YCY 本试卷分第Ⅰ卷和第Ⅱ卷两部分.共 150 分. 第Ⅰ卷（选择题，共 50 分） 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的，请把正确答案的代 号填在题后的括号内（每小题 5 分，共 50 分）. 1．以下命题正确的是 （ ） A．两个平面可以只有一个交点 B．一条直线与一个平面最多有一个公共点 C．两个平面有一个公共点，它们可能相交 D．两个平面有三个公共点，它们一定重合 2．下面四个说法中，正确的个数为 （ ） （1）如果两个平面有三个公共点，那么这两个平面重合 （2）两条直线可以确定一个平面 （3）若 M∈α ，M∈β ，α ∩β ＝l，则 M∈l （4）空间中，相交于同一点的三直线在同一平面内 A．1 B．2 C．3 D．4 3．ABCD－A1B1C1D1 是正方体，O 是 B1D1 的中点，直线 A1C 交平面 AB1D1 于点 M，则下 列结论中错误的是 （ ） A．A、M、O 三点共线 B．M、O、A1、A 四点共面 C．A、O、C、M 四点共面 D．B、B1、O、M 四点共面 4．已知平面α 内有无数条直线都与平面β 平行，那么 （ ） A．α ∥β B．α 与β 相交 C．α 与β 重合 D．α ∥β 或α 与β 相交 5．两等角的一组对应边平行，则 （ ） A．另一组对应边平行 B．另一组对应边不平行 C．另一组对应边也不可能垂直 D．以上都不对 6．如图所示，点 S 在平面 ABC 外，SB⊥AC，SB＝AC＝2， E、F 分别是 SC 和 AB 的中点，则 EF 的长是（ ） A．1 B． 2 C． 2 2 D． 2 1 7．平面α ∥平面β ，AB、CD 是夹在α 和β 间的两条线段，E、F 分别为 AB、CD 的中点， 则 EF 与α 的关系是 （ ） A．平行 B．相交 C．垂直 D．不能确定 8．经过平面外两点与这个平面平行的平面 （ ） A．只有一个 B．至少有一个 C．可能没有 D．有无数个 9．已知 ABCD 是空间四边形形，E、F、G、H 分别是 AB、BC、CD、DA 的中点，如果对 角线 AC＝4，BD＝2，那么 EG2＋HF2 的值等于 （ ） A．10 B．15 C．20 D．25 10．若三个平面把空间分成 6 个部分，那么这三个平面的位置关系是 （ ） A．三个平面共线； B．有两个平面平行且都与第三个平面相交； C．三个平面共线，或两个平面平行且都与第三个平面相交； D．三个平面两两相交。 第Ⅱ卷（非选择题，共 100 分） 二、填空题：请把答案填在题中横线上（每小题 6 分，共 24 分）． 11．如图所示，平面 M、N 互相垂直，棱 l 上有两点 A、B， ACM，BD  N，且 AC⊥l，AB＝8cm，AC＝6 cm， BD＝24 cm，则 CD＝_________． 12．如图所示，A 是△BCD 所在平面外一点，M、N 分别是 △ABC 和△ACD 的重心，若 BD＝6，则 MN＝___________． 13．已知平面α ∥平面β ，P 是α 、β 外一点，过 P 点的两条直 线 PAC、PBD 分别交α 于 A、B，交β 于 C、D，且 PA=6， AC=9，AB=8，则 CD 的长为___________． 14．在棱长为 a 的正方体 ABCD－A1B1C1D1 中，D1 到 B1C 的 距离为_________， A 到 A1C 的距离为_______． 三、解答题：解答应写出文字说明、证明过程或演算步骤(共 76 分). 15．（ 12 分）设 P 是△ABC 所在平面外一点，P 和 A、B、C 的距离相等，∠BAC 为直角. 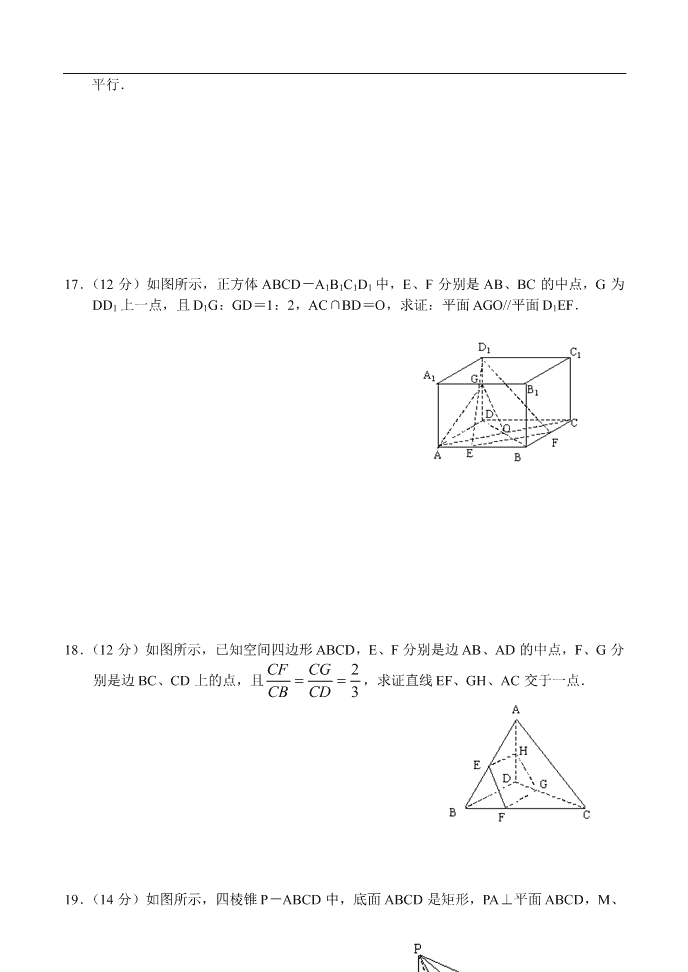求证：平面 PCB⊥平面 ABC． 16．（ 12 分）如图所示，三个平面两两相交，有三条交线，求证这三条交线交于一点或互相 平行． 17．（ 12 分）如图所示，正方体 ABCD－A1B1C1D1 中，E、F 分别是 AB、BC 的中点，G 为 DD1 上一点，且 D1G：GD＝1：2，AC∩BD＝O，求证：平面 AGO//平面 D1EF． 18．（ 12 分）如图所示，已知空间四边形 ABCD，E、F 分别是边 AB、AD 的中点，F、G 分 别是边 BC、CD 上的点，且 3 2 CD CG CB CF ，求证直线 EF、GH、AC 交于一点． 19．（ 14 分）如图所示，四棱锥 P－ABCD 中，底面 ABCD 是矩形，PA⊥平面 ABCD，M、 N 分别是 AB、PC 的中点，PA＝AD＝a． （1）求证：MN∥平面 PAD； （2）求证：平面 PMC⊥平面 PCD． 20．（ 14 分）如图 2－72，棱长为 a 的正方体 ABCD－A1B1C1D1 中，E、F 分别是 B1C1、C1D1 的中点， （1）求证：E、F、B、D 四点共面； （2）求四边形 EFDB 的面积． 参考答案（四） 一、CADDD BACAC 二、11．26 cm；12．2；13．20 或 4；14． 2 6 a ， 3 6 a； 三、15．证明：如答图所示，取 BC 的中点 D，连结 PD、AD， ∵D 是直角三角形 ABC 的斜边 BC 的中点 ∴BD=CD=AD，又 PA=PB=PC，PD 是公共边 ∴∠PDA=∠PDB=∠POC=90° ∴PD⊥BC，PD⊥DA，PD⊥平面 ABC ∴又 PD  平面 PCB ∴平面 PCB⊥平面 ABC. 16．证明：如答图所示，设已知平面α 、β 、γ ， P B D C A P l1 l2 l3 γ α β l3 l2 l1 α γ β (a) (b) α ∩β ＝l1，β ∩γ ＝l2，α ∩γ ＝l3，如果 l1、 l2、 l3 中有任意两条交于一点 P，设 l1∩ l2＝P，即 P∈l1， P∈l2，那么 P∈α ，P∈γ ，则点 P 在平面α 、γ 的 交线 l3 上，即 l1、 l2、 l3 交于一点如（a）图；如果 l1、 l2、 l3 中任何两条都不相交，那么，因为任意两条都共 面，所以 l1∥ l2∥ l3 如（b）图. 17．如答图所示，设 EF∩BD＝H，在△DD1H 中， 13 2 DD DG DH DO  ， ∴GO//D1H，又 GO  平面 D1EF，D1H  平面 D1EF， ∴GO//平面 D1EF， 在△BAO 中，BE＝EF，BH＝HO，∴EH//AO AO 平面 D1EF，EH 平面 D1EF，∴AO//平面 D1EF， AO∩GO＝O，∴平面 AGO//平面 D1EF. 18．如答图所示，∵AE＝EB，AH＝HD，∴EH//BD，且 EH＝ 2 1 BD， ∵ 3 2 CD CG CB CF ，∴FG//BD，且 FG＝ 3 2 BD， ∴EH//FG，且 EH≠FG， 故四边形 EFGH 为梯形，则 EF 与 GH 必相交， 设交点为 P，P∈平面 ABC，又 P∈平面 DAC， 又平面 BAC∩平面 DAC＝AC，故 P∈AC， 即 EF、GH、AC 交于一点. 19．证明：如答图所示，⑴设 PD 的中点为 E，连结 AE、NE， 由 N 为 PD 的中点知 EN // DC， 又 ABCD 是矩形，∴DC // AB，∴EN // 2 1 AB 又 M 是 AB 的中点，∴EN // AN， ∴AMNE 是平行四边形 ∴MN∥AE，而 AE  平面 PAD，NM  平面 PAD ∴MN∥平面 PAD 证明：⑵∵PA＝AD，∴AE⊥PD， 又∵PA⊥平面 ABCD，CD  平面 ABCD， ∴CD⊥PA，而 CD⊥AD，∴CD⊥平面 PAD ∴CD⊥AE， ∵PD∩CD＝D，∴AE⊥平面 PCD， ∵MN∥AE，∴MN⊥平面 PCD， 又 MN 平面 PMC， ∴平面 PMC⊥平面 PCD. B F C G H A E D P N C B M A D E 20． ⑴证明：如答图所示，连结 B1D1，在△C1B1D1 中，C1E＝EB1，C1F＝FD1 ，∴ EF//B1D1，且 EF＝ 2 1 B1D1， 又 A1A // B1B，A1A // D1D，∴B1B // D1D，∴四边形 BB1D1D 是平行四边形. ∴B1D//BD，EF//BD， ∴E、F、D、B 四点共面 ⑵由 AB＝a，知 BD＝B1D1＝ 2 a，EF＝ 2 2 a， DF＝BE＝ 2 1 2 1 EBBB  ＝ aaa 2 5 2 2 2      ， 过 F 作 FH⊥DB 于 H，则 DH＝ aEFDB 4 2 2  ∴FH＝ aaaaDHDF 4 23 16 18 16 2 4 5 22222  四边形的面积为 aaaFHBDEFSEFBD 4 23)22 2(2 1)(2 1  ＝ 22 8 9 4 23 2 23 2 1 aa  A B C D A1 D1 C1 B1 F E H G