- 210.50 KB
- 2021-06-24 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
专题层级快练(十八)
(第一次作业)
1.函数f(x)=ex(sinx+cosx)在区间[0,]上的值域为( )
A.[,e] B.(,e)
C.[1,e] D.(1,e)
答案 A
解析 f′(x)=ex(sinx+cosx)+ex(cosx-sinx)=excosx,当0≤x≤时,f′(x)≥0.
∴f(x)是[0,]上的增函数.∴f(x)的最大值为f()=e,f(x)的最小值为f(0)=.
2.函数f(x)的图像如图所示,下列数值排序正确的是( )
A.00;
当-20,则xf′(x)<0;当x>0时,xf′(x)>0.
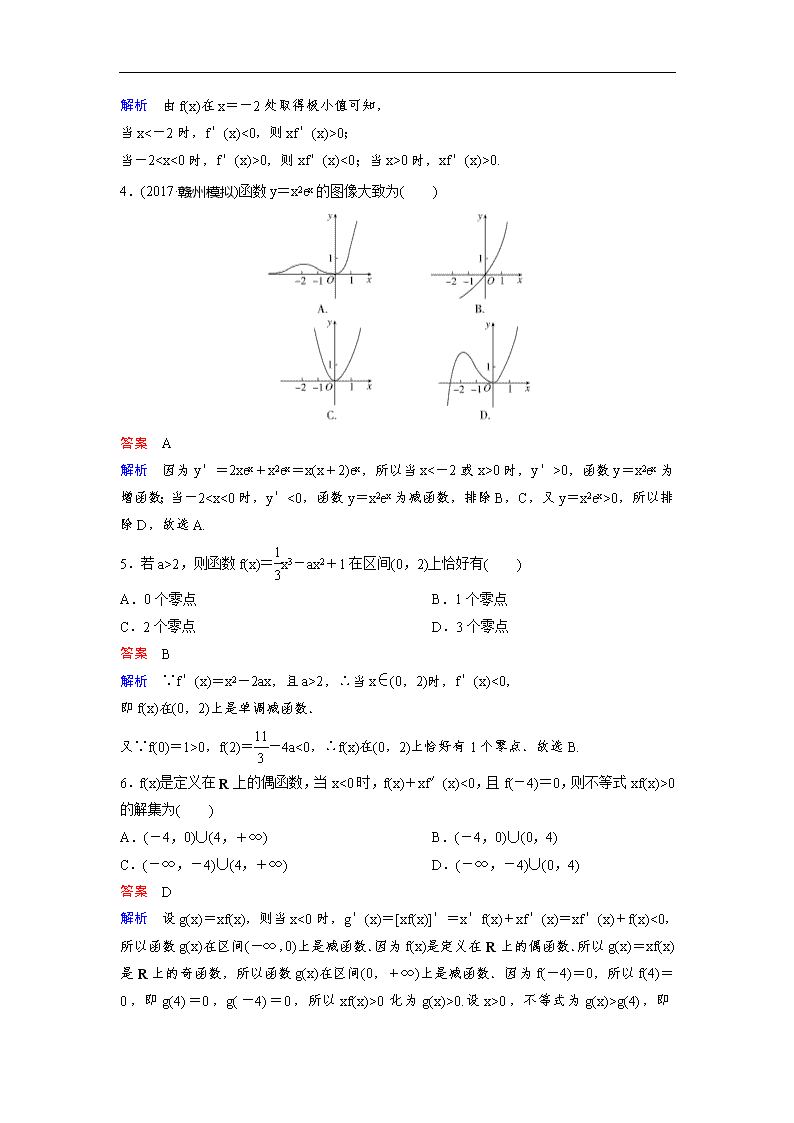
4.(2017·赣州模拟)函数y=x2ex的图像大致为( )
答案 A
解析 因为y′=2xex+x2ex=x(x+2)ex,所以当x<-2或x>0时,y′>0,函数y=x2ex为增函数;当-20,所以排除D,故选A.
5.若a>2,则函数f(x)=x3-ax2+1在区间(0,2)上恰好有( )
A.0个零点 B.1个零点
C.2个零点 D.3个零点
答案 B
解析 ∵f′(x)=x2-2ax,且a>2,∴当x∈(0,2)时,f′(x)<0,
即f(x)在(0,2)上是单调减函数.
又∵f(0)=1>0,f(2)=-4a<0,∴f(x)在(0,2)上恰好有1个零点.故选B.
6.f(x)是定义在R上的偶函数,当x<0时,f(x)+xf′(x)<0,且f(-4)=0,则不等式xf(x)>0的解集为( )
A.(-4,0)∪(4,+∞) B.(-4,0)∪(0,4)
C.(-∞,-4)∪(4,+∞) D.(-∞,-4)∪(0,4)
答案 D
解析 设g(x)=xf(x),则当x<0时,g′(x)=[xf(x)]′=x′f(x)+xf′(x)=xf′(x)+f(x)<0,所以函数g(x)在区间(-∞,0)上是减函数.因为f(x)是定义在R上的偶函数.所以g(x)=xf(x)是R上的奇函数,所以函数g(x)在区间(0,+∞)上是减函数.因为f(-4)=0,所以f(4)=0,即g(4)=0,g(-4)=0,所以xf(x)>0化为g(x)>0.设x>0,不等式为g(x)>g(4),即0g(-4),即x<-4,所求的解集为(-∞,-4)∪(0,4).故选D.
7.已知函数f(x)的定义域为R,f(-1)=2,且对任意的x∈R,f′(x)>2,则f(x)>2x+4的解集为( )
A.(-1,1) B.(-1,+∞)
C.(-∞,-1) D.(-∞,+∞)
答案 B
解析 设g(x)=f(x)-(2x+4),[f(x)-(2x+4)]′=f′(x)-2>0,所以g(x)单调递增.又g(-1)=0,所以f(x)>2x+4的解集是(-1,+∞).故选B.
8.(2017·山东师大附中检测)已知函数f(x)=xex,g(x)=-(x+1)2+a,若∃x1,x2∈R,使得f(x2)≤g(x1)成立,则实数a的取值范围是( )
A.(-,+∞) B.[-1,+∞)
C.[-e,+∞) D.[-,+∞)
答案 D
解析 f′(x)=ex+xex=(1+x)ex,当x>-1时,f′(x)>0,函数单调递增;当x<-1时,f′(x)<0,函数单调递减.所以当x=-1时,f(x)取得极小值即最小值,f(-1)=-.函数g(x)的最大值为a.若∃x1,x2∈R,使得f(x2)≤g(x1)成立,则有g(x)的最大值大于或等于f(x)的最小值,即a≥-.故选D.
9.已知函数y=f(x)对任意的x∈(-,)满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是( )
A.f(-)2f() D.f(0)>f()
答案 A
解析 由f′(x)cosx+f(x)sinx>0知()′>0,所以g(x)=在(-,)上是增函数,所以g(-)g(),即>,得f()>f(),所以B不正确;由g()>g(0),即>
eq f(f(0),cos0),得f(0)<2f(),所以C不正确;由g()>g(0),即>,得f(0)0时,f(x)=xe-x,f′(x)=-(x-1)e-x,若00,f(x)是增函数;若x>1,则f′(x)<0,f(x)是减函数.因此,要使关于x的方程f2(x)-mf(x)+m-1=0恰好有4个不相等的实数根,只要求直线y=1,直线y=m-1与函数y=f(x)的图像共有四个不同的交点.注意到直线y=1与函数y=f(x)的图像有唯一公共点,因此要求直线y=m-1与函数y=f(x)的图像共有三个不同的交点,结合图像可知,00,所以当x>2时,f′(x)>0;当00时原方程有唯一解,所以函数y=h(x)与y=m的图像在y轴右侧有唯一的交点.
又h′(x)=4x--14=,且x>0,
所以当x>4时,h′(x)>0;当00时原方程有唯一解的充要条件是m=h(4)=-16ln2-24.
14.(2017·衡水中学调研卷)已知函数f(x)=x2+alnx.
(1)若a=-1,求函数f(x)的极值,并指出是极大值还是极小值;
(2)若a=1,求函数f(x)在[1,e]上的最大值和最小值;
(3)若a=1,求证:在区间[1,+∞)上函数f(x)的图像在函数g(x)=x3的图像的下方.
答案 (1)极小值为 (2)f(x)min=,f(x)max=e2+1 (3)略
解析 (1)由于函数f(x)的定义域为(0,+∞),
当a=-1时,f′(x)=x-=,
令f′(x)=0,得x=1或x=-1(舍去).
当x∈(0,1)时,函数f(x)单调递减,
当x∈(1,+∞)时,函数f(x)单调递增,
所以f(x)在x=1处取得极小值,极小值为.
(2)当a=1时,易知函数f(x)在[1,e]上为增函数,
所以f(x)min=f(1)=,f(x)max=f(e)=e2+1.
(3)证明:设F(x)=f(x)-g(x)=x2+lnx-x3,
则F′(x)=x+-2x2=,
当x>1时,F′(x)<0,故F(x)在区间(1,+∞)上是减函数.又因为F(1)=-<0,所以在区间[1,+∞)上F(x)<0恒成立,即f(x)0时,对∀x>0,不等式f(x)-g(x)≥1恒成立,求实数a的取值范围.
答案 (1)x0=1 (2)[1,+∞)
解析 (1)f′(x)=a+,g′(x)=.
由题意知x0>0,f′(x0)=g′(x0),即a+=.
所以ax02-x0+1-a=0,所以a(x02-1)+(1-x0)=0.
因为上式对任意实数a恒成立,所以所以x0=1.
(2)f(x)-g(x)≥1,即ax+-lnx≥1.
记h(x)=ax+-lnx,则在(0,+∞)上h(x)≥1,
当a>0时,h′(x)=a+-==(x>0).
①若00,h(x)单调递增,h(x)0,h(x)单调递增,而h(1)=2a-1<1,
这与在(0,+∞)上h(x)≥1矛盾;
③若a≥1,-1+≤0,所以x∈(0,1)时,h′(x)<0,h(x)单调递减;x∈(1,+∞)时,h′(x)>0,h(x)单调递增,所以h(x)min=h(1)=2a-1≥1,即h(x)≥1恒成立.
综上所述,实数a的取值范围是[1,+∞).
2.已知函数f(x)=lnx-.
(1)求函数f(x)的单调递增区间;
(2)证明:当x>1时,f(x)1,当x∈(1,x0)时,恒有f(x)>k(x-1).
答案 (1)增区间(0,) (2)略 (3)(-∞,1)
解析 (1)f′(x)=-x+1=,x∈(0,+∞).
由f′(x)>0得解得01时,F(x)1时,f(x)1满足题意.
当k>1时,对于x>1,有f(x)1满足题意.
当k<1时,令G(x)=f(x)-k(x-1),x∈(0,+∞),
则有G′(x)=-x+1-k=.
由G′(x)=0得-x2+(1-k)x+1=0.
解得x1=<0,
x2=>1.
当x∈(1,x2),G′(x)>0,故G(x)在[1,x2)上单调递增.
从而当x∈(1,x2)时,G(x)>G(1)=0,即f(x)>k(x-1).
综上所述,k的取值范围是(-∞,1).
3.已知函数f(x)=ex-ax(a为常数)的图像与y轴交于点A,曲线y=f(x)在点A处的切线斜率为-1.
(1)求a的值及函数f(x)的极值;
(2)证明:当x>0时,x2<ex.
答案 (1)a=2,极小值为f(ln2)=2-ln4 (2)略
解析 (1)由f(x)=ex-ax,得f′(x)=ex-a.
又f′(0)=1-a=-1,得a=2.
所以f(x)=ex-2x,f′(x)=ex-2.
令f′(x)=0,得x=ln2.
当x<ln2时,f′(x)<0,f(x)单调递减;当x>ln2时,f′(x)>0,f(x)单调递增.
所以当x=ln2时,f(x)取得极小值,且极小值为f(ln2)=eln2-2ln2=2-ln4,
f(x)无极大值.
(2)令g(x)=ex-x2,则g′(x)=ex-2x,由(1)得g′(x)=f(x)≥f(ln2)>0,
故g(x)在R上单调递增.又g(0)=1>0,因此,当x>0时,g(x)>g(0)>0,即x2<ex.
4.(2017·沧州七校联考)设f(x)=ex-a(x+1).
(1)若∀x∈R,f(x)≥0恒成立,求正实数a的取值范围;
(2)设g(x)=f(x)+,且A(x1,y1),B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的a≤-1,直线AB的斜率恒大于常数m,求m的取值范围.
答案 (1)(0,1] (2)(-∞,3]
解析 (1)因为f(x)=ex-a(x+1),所以f′(x)=ex-a.
由题意,知a>0,故由f′(x)=ex-a=0,解得x=lna.
故当x∈(-∞,lna)时,f′(x)<0,函数f(x)单调递减;当x∈(lna,+∞)时,f′(x)>0,函数f(x)单调递增.
所以函数f(x)的最小值为f(lna)=elna-a(lna+1)=-alna.
由题意,若∀x∈R,f(x)≥0恒成立,即f(x)=ex-a(x+1)≥0恒成立,故有-alna≥0,
又a>0,所以lna≤0,解得0m,即>m.
因为x2-x1>0,所以g(x2)-g(x1)>m(x2-x1),即g(x2)-mx2>g(x1)-mx1,
因为x12;④a=0,b=2;⑤a=1,b=2.
答案 ①③④⑤
解析 令f(x)=x3+ax+b,则f′(x)=3x2+a.
对于①,由a=b=-3,得f(x)=x3-3x-3,f′(x)=3(x+1)(x-1),f(x)极大值=f(-1)=-1<0,f(x)极小值=f(1)=-5<0,函数f(x)的图像与x轴只有一个交点,故x3+ax+b=0仅有一个实根;
对于②,由a=-3,b=2,得f(x)=x3-3x+2,f′(x)=3(x+1)(x-1),f(x)极大值=f(-1)=4>0,f(x)极小值=f(1)=0,函数f(x)的图像与x轴有两个交点,故x3+ax+b=0有两个实根;
对于③,由a=-3,b>2,得f(x)=x3-3x+b,f′(x)=3(x+1)(x-1),f(x)极大值=f(-1)=2+b>0,f(x)极小值=f(1)=b-2>0,函数f(x)的图像与x轴只有一个交点,故x3+ax+b=0仅有一个实根;
对于④,由a=0,b=2,得f(x)=x3+2,f′(x)=3x2≥0,f(x)在R上单调递增,函数f(x)的图像与x轴只有一个交点,故x3+ax+b=0仅有一个实根;对于⑤,由a=1,b=2,得f(x)=x3+x+2,f′(x)=3x2+1>0,f(x)在R上单调递增,函数f(x)的图像与x轴只有一个交点,故x3+ax+b=0仅有一个实根.
2.(2017·西城区期末)已知函数f(x)=(x+a)ex,其中e是自然对数的底数,a∈R.
(1)求函数f(x)的单调区间;
(2)当a<1时,试确定函数g(x)=f(x-a)-x2的零点个数,并说明理由.
答案 (1)单调递减区间为(-∞,-a-1),单调递增区间为(-a-1,+∞)
(2)仅有一个零点
解析 (1)因为f(x)=(x+a)ex,x∈R,所以f′(x)=(x+a+1)ex.
令f′(x)=0,得x=-a-1.
当x变化时,f(x)和f′(x)的变化情况如下:
x
(-∞,-a-1)
-a-1
(-a-1,+∞)
f′(x)
-
0
+
f(x)
故f(x)的单调递减区间为(-∞,-a-1),单调递增区间为(-a-1,+∞).
(2)结论:函数g(x)有且仅有一个零点.
理由如下:
由g(x)=f(x-a)-x2=0,得方程xex-a=x2,
显然x=0为此方程的一个实数解,
所以x=0是函数g(x)的一个零点.
当x≠0时,方程可化简为ex-a=x.
设函数F(x)=ex-a-x,则F′(x)=ex-a-1,
令F′(x)=0,得x=a.
当x变化时,F(x)与F′(x)的变化情况如下:
x
(-∞,a)
a
(a,+∞)
F′(x)
-
0
+
F(x)
即F(x)的单调递增区间为(a,+∞),单调递减区间为(-∞,a).
所以F(x)的最小值F(x)min=F(a)=1-a.
因为a<1,所以F(x)min=F(a)=1-a>0,
所以对于任意x∈R,F(x)>0,
因此方程ex-a=x无实数解.
所以当x≠0时,函数g(x)不存在零点.
综上,函数g(x)有且仅有一个零点.
3.设函数f(x)=-x3+x2+(a2-1)x,其中a>0.
(1)若函数y=f(x)在x=-1处取得极值,求a的值;
(2)已知函数f(x)有3个不同的零点,分别为0,x1,x2,且x1f(1)恒成立,求a的取值范围.
答案 (1)a=2 (2)(,)
解析 (1)f′(x)=-x2+2x+(a2-1),
因为y=f(x)在x=-1处取得极值,所以f′(-1)=0.
即-(-1)2+2(-1)+(a2-1)=0.
解得a=±2.经检验得a=2.
(2)由题意得f(x)=x(-x2+x+a2-1)=-x(x-x1)(x-x2).
所以方程-x2+x+a2-1=0有两个相异的实根x1,x2.
故Δ=1+(a2-1)>0,解得a<-(舍去)或a>,且x1+x2=3.
又因为x1x1+x2=3,故x2>>1.
①若x1≤1f(1)恒成立的充要条件为f(1)=a2-<0,解得-0时,f(x)≥2a+aln.
答案 (1)当a≤0时,f′(x)没有零点,当a>0时,f′(x)有唯一零点. (2)略
解析 (1)f(x)的定义域为(0,+∞),f′(x)=2e2x-(x>0).
当a≤0时,f′(x)>0,f′(x)没有零点;
当a>0时,因为y=e2x单调递增,y=-单调递增,所以f′(x)在(0,+∞)上单调递增,又f′(a)>0,当b满足00时,f′(x)存在唯一零点.
(2)由(1),可设f′(x)在(0,+∞)上的唯一零点为x0,当x∈(0,x0)时,f′(x)<0,当x∈(x0,+∞)时,f′(x)>0.
故f(x)在(0,x0)上单调递减,在(x0,+∞)上单调递增,所以当x=x0时,f(x)取得最小值,最小值为f(x0).
由于2e2x0-=0,所以f(x0)=+2ax0+aln≥2a+aln.
故当a>0时,f(x)≥2a+aln.
5.已知函数f(x)=x-ln(x+a)在x=1处取得极值.
(1)求实数a的值;
(2)若关于x的方程f(x)+2x=x2+b在[,2]上恰有两个不相等的实数根,求实数b的取值范围.
答案 (1)0 (2)+ln2≤b<2
解析 (1)对f(x)求导,得f′(x)=1-.
由题意,得f′(1)=0,即1-=0,∴a=0.
(2)由(1)得f(x)=x-lnx.∴f(x)+2x=x2+b,即x2-3x+lnx+b=0.
设g(x)=x2-3x+lnx+b(x>0),则
g′(x)=2x-3+==.
令g′(x)=0,得x1=,x2=1.
当x变化时,g′(x),g(x)的变化情况如下表:
x
(0,)
(,1)
1
(1,2)
2
g′(x)
+
0
-
0
+
+
g(x)
极大值
极小值
b-2+ln2
∴当x=1时,g(x)的极小值为g(1)=b-2.
又g()=b--ln2,g(2)=b-2+ln2,
∵方程f(x)+2x=x2+b在[,2]上恰有两个不相等的实数根,
∴即解得+ln2≤b<2.
6.(2017·皖南十校联考)设函数f(x)=lnx+ax2+x-a-1(a∈R).
(1)当a=-时,求函数f(x)的单调区间;
(2)证明:当a≥0时,不等式f(x)≥x-1在[1,+∞)上恒成立.
答案 (1)增区间为(0,],减区间为[,+∞)
(2)略
解析 (1)当a=-时,f(x)=lnx-x2+x-,且定义域为(0,+∞),
因为f′(x)=-x+1=-,
当x∈(0,)时,f′(x)>0;当x∈(,+∞)时,f′(x)<0,
所以f(x)在(0,]上是增函数;在[,+∞)上是减函数.
(2)令g(x)=f(x)-x+1=lnx+ax2-a,则g′(x)=+2ax=,
所以当a≥0时,g′(x)>0在[1,+∞)上恒成立,
所以g(x)在[1,+∞)上是增函数,且g(1)=0,
所以g(x)≥0在[1,+∞)上恒成立,
即当a≥0时,不等式f(x)≥x-1在[1,+∞)上恒成立.