高考数学专题复习练习第3讲 直线与圆、圆与圆的位置关系 8页

第3讲 直线与圆、圆与圆的位置关系 一、选择题 ‎1．已知集合A＝{(x，y)|x，y为实数，且x2＋y2＝1}，B＝{(x，y)|x，y为实数，且x＋y＝1}，则A∩B的元素个数为(　　)．‎ A．4 B．‎3 C．2 D．1‎ 解析　法一　(直接法)集合A表示圆，集合B表 示一条直线，又圆心(0,0)到直线x＋y＝1的距离 d＝＝＜1＝r，所以直线与圆相交，故选C.‎ 法二　(数形结合法)画图可得，故选C.‎ 答案　C ‎2．若直线x－y＋1＝0与圆(x－a)2＋y2＝2有公共点，则实数a的取值范围是 (　　)．‎ A．[－3，－1] B．[－1,3]‎ C．[－3,1] D．(－∞，－3]∪[1，＋∞)‎ 解析　由题意可得，圆的圆心为(a,0)，半径为，‎ ‎∴≤，即|a＋1|≤2，解得－3≤a≤1.‎ 答案　C ‎3．若圆(x－a)2＋(y－b)2＝b2＋1始终平分圆(x＋1)2＋(y＋1)2＝4的周长，则a，b满足的关系是(　　)‎ A．a2＋‎2a＋2b－3＝0‎ B．a2＋b2＋‎2a＋2b＋5＝0‎ C．a2＋‎2a＋2b＋5＝0‎ D．a2－‎2a－2b＋5＝0‎ 解析 即两圆的公共弦必过(x＋1)2＋(y＋1)2＝4的圆心，‎ 两圆相减得相交弦的方程为－2(a＋1)x－2(b＋1)y＋a2＋1＝0，‎ 将圆心坐标(－1，－1)代入可得a2＋‎2a＋2b＋5＝0.‎ 答案　C ‎4．若圆C1：x2＋y2＋2ax＋a2－4＝0(a∈R)与圆C2：x2＋y2－2by－1＋b2＝0(b∈R)恰有三条切线，则a＋b的最大值为 (　　)．‎ A．－3 B．－‎3 ‎ C．3 D．3 解析　易知圆C1的圆心为C1(－a,0)，半径为r1＝2；‎ 圆C2的圆心为C2(0，b)，半径为r2＝1.‎ ‎∵两圆恰有三条切线，∴两圆外切，‎ ‎∴|C‎1C2|＝r1＋r2，即a2＋b2＝9.∵2≤，‎ ‎∴a＋b≤3(当且仅当a＝b＝时取“＝”)，‎ ‎∴a＋b的最大值为3.‎ 答案　D ‎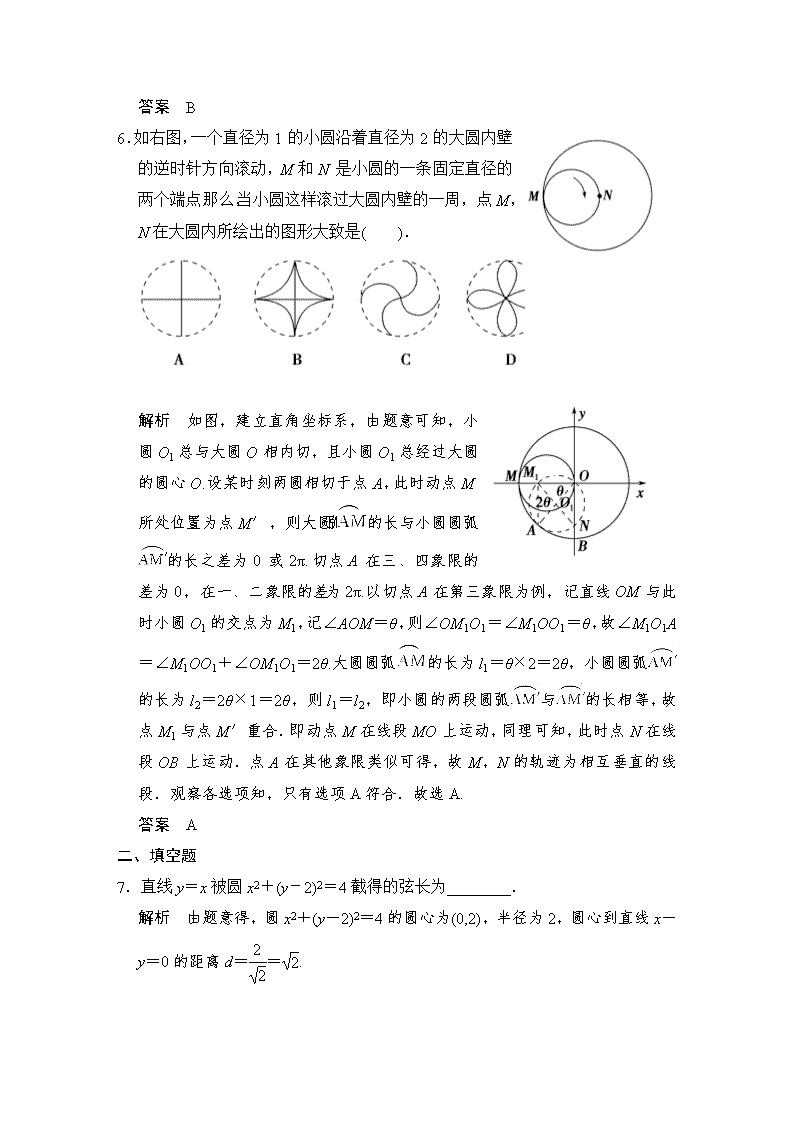5．若曲线C1：x2＋y2－2x＝0与曲线C2：y(y－mx－m)＝0有四个不同的交点，则实数m的取值范围是 (　　)． ‎ A. B.∪ C. D.∪ 解析　C1：(x－1)2＋y2＝1，C2：y＝0或y＝mx＋m＝m(x＋1)．‎ 当m＝0时，C2：y＝0，此时C1与C2显然只有两个交点；‎ 当m≠0时，要满足题意，需圆(x－1)2＋y2＝1与直线y＝m(x＋1)有两交点，当圆与直线相切时，m＝±，即直线处于两切线之间时满足题意，‎ 则－2，b>2)．‎ ‎(1)求证：(a－2)(b－2)＝2；‎ ‎(2)求线段AB中点的轨迹方程；‎ ‎(3)求△AOB面积的最小值．‎ 解 (1)证明：圆的标准方程是(x－1)2＋(y－1)2＝1，设直线方程为＋＝1，即bx＋ay－ab＝0，圆心到该直线的距离d＝＝1，‎ 即a2＋b2＋a2b2＋2ab－‎2a2b－2ab2＝a2＋b2，即a2b2＋2ab－‎2a2b－2ab2＝0，‎ 即ab＋2－‎2a－2b＝0，即(a－2)(b－2)＝2.‎ ‎(2)设AB中点M(x，y)，则a＝2x，b＝2y，代入(a－2)(b－2)＝2，‎ 得(x－1)(y－1)＝(x>1，y>1)．‎ ‎(3)由(a－2)(b－2)＝2得ab＋2＝2(a＋b)≥4，‎ 解得≥2＋(舍去≤2－)，‎ 当且仅当a＝b时，ab取最小值6＋4，‎ 所以△AOB面积的最小值是3＋2.‎ ‎13．设直线l的方程为y＝kx＋b(其中k的值与b无关)，圆M的方程为x2＋y2－2x－4＝0.‎ ‎(1)如果不论k取何值，直线l与圆M总有两个不同的交点，求b的取值范围；‎ ‎(2)b＝1时，l与圆交于A，B两点，求|AB|的最大值和最小值．‎ 解　圆M的标准方程为(x－1)2＋y2＝5，‎ ‎∴圆心M的坐标为(1,0)，半径为r＝.‎ ‎(1)∵不论k取何值，直线l总过点P(0，b)，‎ ‎∴欲使l与圆M总有两个不同的交点，必须且只需点P在圆M的内部，即|MP|<，即1＋b2<5，‎ ‎∴－2