高考数学一轮复习练案24第三章三角函数解三角形第五讲函数y＝Asinωx＋φ的图象及应用含解析 10页

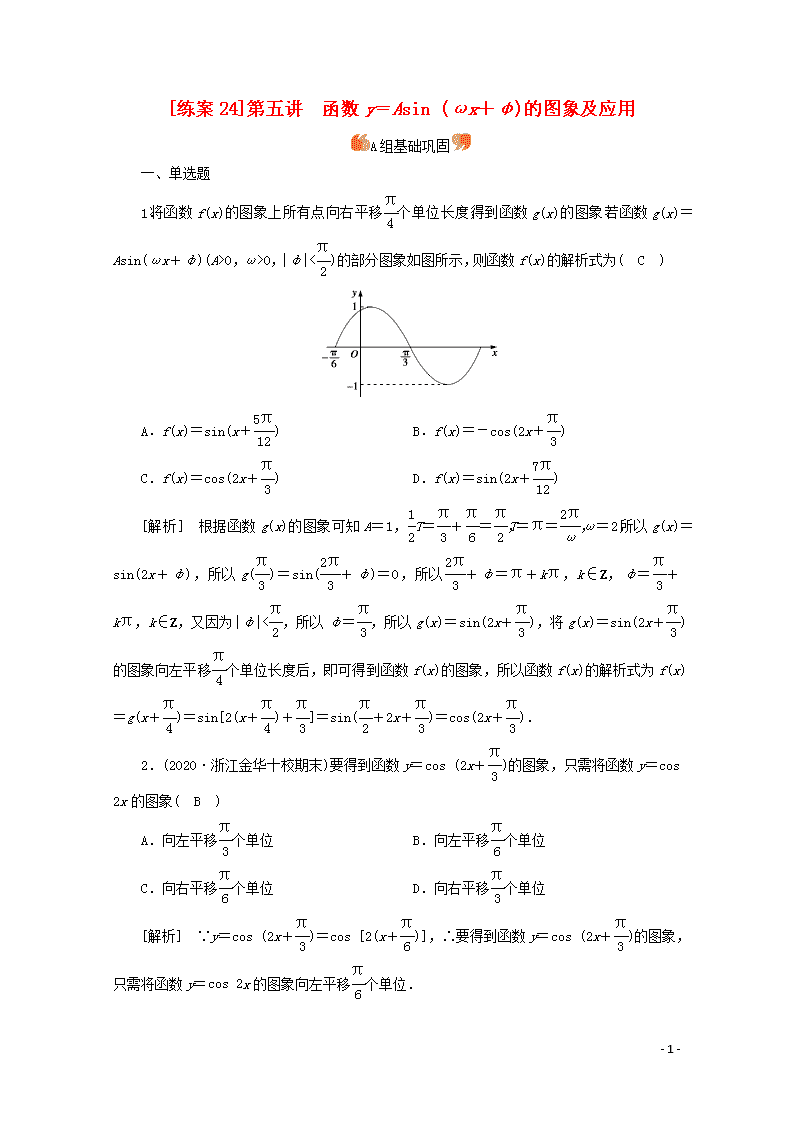
‎ [练案24]第五讲　函数y＝Asin (ωx＋φ)的图象及应用 A组基础巩固 一、单选题 ‎1．将函数f(x)的图象上所有点向右平移个单位长度，得到函数g(x)的图象．若函数g(x)＝Asin(ωx＋φ)(A>0，ω>0，|φ|<)的部分图象如图所示，则函数f(x)的解析式为(　C　)‎ A．f(x)＝sin(x＋)　　 B．f(x)＝－cos(2x＋)‎ C．f(x)＝cos(2x＋)　　 D．f(x)＝sin(2x＋)‎ ‎[解析]　根据函数g(x)的图象可知A＝1，T＝＋＝，T＝π＝，ω＝2，所以g(x)＝sin(2x＋φ)，所以g()＝sin(＋φ)＝0，所以＋φ＝π＋kπ，k∈Z，φ＝＋kπ，k∈Z，又因为|φ|<，所以φ＝，所以g(x)＝sin(2x＋)，将g(x)＝sin(2x＋)的图象向左平移个单位长度后，即可得到函数f(x)的图象，所以函数f(x)的解析式为f(x)＝g(x＋)＝sin[2(x＋)＋]＝sin(＋2x＋)＝cos(2x＋)．‎ ‎2．(2020·浙江金华十校期末)要得到函数y＝cos (2x＋)的图象，只需将函数y＝cos 2x的图象(　B　)‎ A．向左平移个单位　　 B．向左平移个单位 C．向右平移个单位　　 D．向右平移个单位 ‎[解析]　∵y＝cos (2x＋)＝cos [2(x＋)]，∴要得到函数y＝cos (2x＋)的图象，只需将函数y＝cos 2x的图象向左平移个单位．‎ ‎3．(2020·河南豫南九校联考)将函数y＝sin (x－ - 10 -‎ ‎)的图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，再向右平移个单位，则所得函数图象的解析式为(　B　)‎ A．y＝sin (－)　　 B．y＝sin (－)‎ C．y＝sin (－)　　 D．y＝sin (2x－)‎ ‎[解析]　函数y＝sin (x－)经伸长变换得y＝sin (－)，再作平移变换得y＝sin [(x－)－]＝sin (－)．‎ ‎4．(2020·安徽省宿州市高三上学期检测)已知函数f(x)＝Asin (ωx＋φ)(A>0，ω>0,0<φ<)的部分图象如图所示，若将函数f(x)的图象上点的纵坐标不变，横坐标缩短到原来的，再向右平移个单位，所得到的函数g(x)的解析式为(　D　)‎ A．g(x)＝2sin x　　 B．g(x)＝2sin 2x C．g(x)＝2sin (x－)　　 D．g(x)＝2sin (2x－)‎ ‎[解析]　由图象可得A＝2，＝π，故T＝4π，ω＝，‎ ‎∴f(x)＝2sin (x＋φ)，∵点(0,1)在函数的图象上，‎ ‎∴f(0)＝2sin φ＝1，∴sin φ＝，又0<φ<，‎ ‎∴φ＝，∴f(x)＝2sin (x＋)，‎ 将函数f(x)的图象上点的纵坐标不变，横坐标缩短到原来的所得图象对应的解析式为y＝2sin (×4x＋)＝2sin (2x＋)，然后再向右平移个单位，所得图象对应的解析式为y＝2sin [2(x－)＋]＝2sin (2x－)，即g(x)＝2sin (2x－)，选D.‎ ‎5．设函数f(x)＝sin (ωx＋φ)＋cos (ωx＋φ)(ω>0，|φ|<)的最小正周期为π，且f(－x)＝f(x)，则(　A　)‎ A．f(x)在(0，)上单调递减 - 10 -‎ B．f(x)在(0，)上单调递增 C．f(x)在(，)上单调递增 D．f(x)在(，π)上单调递减 ‎[解析]　f(x)＝sin (ωx＋φ)＋cos (ωx＋φ)＝sin (ωx＋φ＋)．‎ 由函数f(x)的最小正周期T＝＝π，得ω＝2.‎ 由f(－x)＝f(x)，得φ＋＝＋kπ(k∈Z)，‎ 即φ＝＋kπ(k∈Z)．‎ 又∵|φ|<，∴φ＝.‎ ‎∴f(x)＝sin (2x＋)＝cos 2x.‎ 若2x∈(0，π)，则x∈(0，)，‎ ‎∴f(x)在(0，)上单调递减．故选A.‎ ‎6．已知曲线C：y＝sin (2x＋φ)(|φ|<)的一条对称轴方程为x＝，曲线C向左平移θ(θ>0)个单位长度，得到的曲线E的一个对称中心为(，0)，则|φ－θ|的最小值是(　A　)‎ A．　 B．　‎ C．　 D． ‎[解析]　因为曲线C：y＝sin (2x＋φ)(|φ|<)的一条对称方程为x＝，所以sin (＋φ)＝±1，则＋φ＝＋kπ，k∈Z.因为|φ|<，所以φ＝.可得曲线C：y＝sin (2x＋)，向左平移θ个单位长度，得曲线E：y＝sin (2x＋2θ＋)．由曲线E的对称中心为(，0)，得2×＋2θ＋＝kπ，k∈Z，所以θ＝kπ－，k∈Z，则|φ－θ|＝(k∈Z)的最小值为：.故选A.‎ 二、多选题 ‎7．(2020·辽宁省实验中学期中改编)已知函数y＝Asin (ωx＋φ)＋B(A>0，ω>0，|φ|<‎ - 10 -‎ )的部分图象如图，则下面不正确的是(　ABC　)‎ A．A＝4　　 B．ω＝1‎ C．B＝4　　 D．φ＝ ‎[解析]　根据函数y＝Asin (ωx＋φ)＋B的图象知，A＝2，B＝2，∴A，C错误；设函数的最小正周期为T，则T＝π－＝，∴T＝＝π，解得ω＝2，B错误；当x＝时，ωx＋φ＝2×＋φ＝2kπ＋(k∈Z)，且|φ|<，∴φ＝，∴D正确．故选A、B、C. ‎ ‎8．已知函数f(x)＝sin ωx＋cos ωx(ω>0)的图象相邻两条对称轴之间的距离是，则该函数的一个单调递增区间为(　AD　)‎ A．[－，]　　 B．[－，]‎ C．[－，]　　 D．[，]‎ ‎[解析]　根据已知得f(x)＝sin ωx＋cos ωx＝2(sin ωx＋cos ωx)＝2sin (ωx＋)．根据相邻两条对称轴之间的距离是，得T＝π，所以＝π，即ω＝2，所以函数f(x)＝2sin (2x＋)．再根据正弦函数的单调性可得该函数的单调递增区间是2kπ－≤2x＋≤2kπ＋(k∈Z)，解得kπ－≤x≤kπ＋(k∈Z)．令k＝0,1即可求得其一个单调递增区间是[－，]、[，]．故选A、D.‎ 三、填空题 ‎9．(1)为了得到函数y＝sin (x＋1)的图象，只需把函数y＝sin x的图象上所有的点向__左__平移__1__个单位长度．‎ ‎(2)为了得到函数y＝sin (2x＋1)的图象，只需把函数y＝sin 2x的图象上所有的点向__左__平移　　个单位长度．‎ - 10 -‎ ‎10．已知函数f(x)＝2sin (x＋φ)(|φ|<)的图象经过点(0,1)，则该函数的振幅为__2，周期T为__6，频率为　　，初相φ为　　.‎ ‎[解析]　振幅A＝2，T＝＝6，f＝，因为图象过点(0,1)，所以1＝2sin φ，所以sin φ＝，又|φ|<，所以φ＝.‎ ‎11．(2020·南昌模拟)将函数f(x)＝sin (ωx＋φ)(ω>0，－<φ<)图象上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移个单位长度得到y＝sin x的图象，则f()＝　　.‎ ‎[解析]　将y＝sin x的图象向左平移个单位长度，再把横坐标伸长到原来的2倍，纵坐标不变，得f(x)＝sin (x＋)，所以f()＝sin (·＋)＝sin ＝.‎ ‎12．(2020·重庆模拟)已知函数y＝Asin (ωx＋φ)(A>0，ω>0，|φ|<)的图象上有一个最高点的坐标为(2，)，由这个最高点到其右侧相邻最低点间的图象与x轴交于点(6,0)，则此解析式为　y＝sin (x＋)　.‎ ‎[解析]　由题意得：A＝，＝6－2，T＝16，ω＝＝，又sin (×2＋φ)＝1，＋φ＝＋2kπ(k∈Z)，‎ 又|φ|<，所以φ＝，‎ 所以函数解析式为y＝sin (x＋)．‎ 四、解答题 ‎13．(2020·江西南昌实验中学月考)已知函数f(x)＝2sin (x＋)．‎ ‎(1)用“五点法”在如图所示的虚线方框内作出函数f(x)在一个周期内的简图(要点：列表与描点，建立直角坐标系)；‎ - 10 -‎ ‎(2)函数f(x)的图象可以通过函数g(x)＝2cos x的图象经过“先伸缩后平移”的规则变换而得到，请写出一个这样的变换．‎ ‎[解析]　(1)列表如下：‎ x ‎－ x＋ ‎0‎ π ‎2π f(x)‎ ‎0‎ ‎2‎ ‎0‎ ‎－2‎ ‎0‎ 图象如图所示：‎ ‎(2)g(x)＝2cos x＝2sin (x＋)，先将横坐标伸长为原来的2倍，得到y＝2sin (＋)，再向右平移个单位，得到f(x)＝2sin (x＋)．(答案不唯一)‎ ‎14．(2020·河北沧州模拟)已知函数f(x)＝Asin (ωx＋φ)(A>0，ω>0，|φ|<)的部分图象如图所示．‎ ‎(1)求函数f(x)的解析式，并求它的对称中心的坐标；‎ ‎(2)将函数f(x)的图象向右平移m(0，即＝>，得cos 2ω<0，所以ω＝2.故选B.‎ ‎3．(多选题)(2020·吉林通化月考改编)已知ω>0，a>0，f(x)＝asin ωx＋acos ωx，g(x)＝2cos (ax＋)，h(x)＝.这3个函数在同一直角坐标系中的部分图象如图所示，则函数g(x)＋h(x)的图象的一条对称轴方程可以为(　AC　)‎ A．x＝　　 B．x＝ C．x＝－　　 D．x＝－ ‎[解析]　∵f(x)＝asin ωx＋acos ωx＝2asin (ωx＋)，g(x)＝2cos (ax＋)，又由函数图象可知，f(x)的最大值为2，可得a＝1，∴f(x)＝2sin (ωx＋)，g(x)＝2cos (x＋ - 10 -‎ ‎)，由图象可知，f(x)的周期为π，∴ω＝2，h(x)＝＝＝2sin (x＋)，x≠kπ＋(k∈Z)．那么函数g(x)＋h(x)＝2cos (x＋)＋2sin (x＋)＝2sin (x＋＋)＝2sin (x＋)，x≠kπ＋(k∈Z)．令x＋＝＋kπ(k∈Z)．可得对称轴方程为x＝＋kπ(k∈Z)，当k＝0时，x＝，当k＝－2时，可得x＝－.故选A、C. ‎ ‎4．(2020·四川达州高级中学诊断)已知f(x)＝2sin (2x－)－m在x∈[0，]上有两个零点，则实数m的取值范围为(　C　)‎ A．(1,2)　 B．[1,2]　‎ C．[1,2)　 D．(1,2]‎ ‎[解析]　f(x)＝2sin (2x－)－m＝0，‎ 即m＝2sin (2x－)‎ 记g(x)＝2sin (2x－)，x∈[0，]‎ 其图象如下图，由图可知m的取值范围是[1,2)，故选C.‎ ‎5．某同学用“五点法”画函数f(x)＝Asin (ωx＋φ)(ω>0，|φ|<)在某一个周期内的图象时，列表并填入了部分数据，如下表：‎ ωx＋φ ‎0‎ π ‎2π x Asin (ωx＋φ)‎ ‎0‎ ‎5‎ ‎－5‎ ‎0‎ ‎(1)请将上表数据补充完整，并直接写出函数f(x)的解析式．‎ ‎(2)将y＝f(x)图象上所有点向左平行移动θ(θ>0)个单位长度，得到y＝g(x)的图象．若y＝g(x)图象的一个对称中心为(，0)，求θ的最小值．‎ - 10 -‎ ‎[解析]　(1)根据表中已知数据，解得A＝5，ω＝2，φ＝－.数据补全如下：‎ ωx＋φ ‎0‎ π ‎2π x Asin (ωx＋φ)‎ ‎0‎ ‎5‎ ‎0‎ ‎－5‎ ‎0‎ 且函数表达式为f(x)＝5sin (2x－)．‎ ‎(2)由(1)知f(x)＝5sin (2x－)，‎ 得g(x)＝5sin (2x＋2θ－)．‎ 因为y＝sin x图象的对称中心为(kπ，0)，k∈Z，‎ 所以令2x＋2θ－＝kπ，k∈Z，‎ 解得x＝＋－θ，k∈Z.‎ 由于函数y＝g(x)图象的一个对称中心为(，0)，‎ 令＋－θ＝，k∈Z，‎ 解得θ＝－，k∈Z.‎ 由θ>0可知，当k＝1时，θ取得最小值.‎ - 10 -‎