2021高考数学新高考版一轮习题：专题7 第51练 空间几何体的结构特征、三视图与直观图 Word版含解析 6页

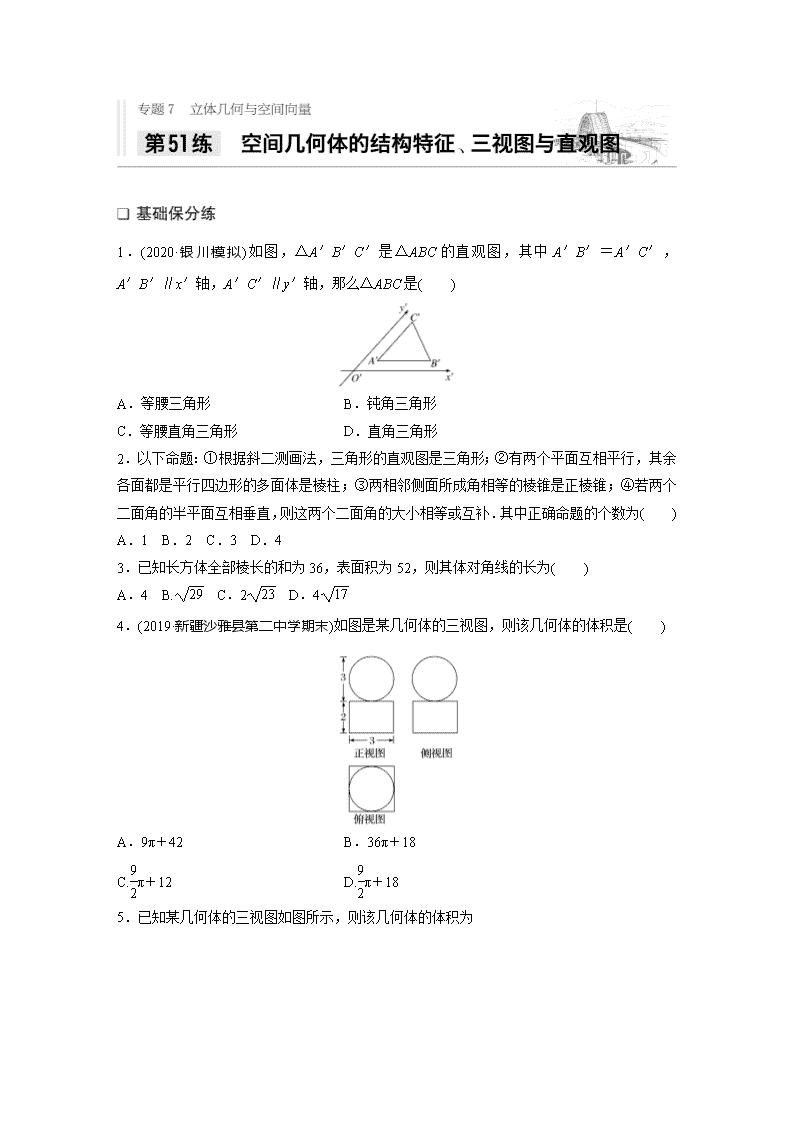
‎1．(2020·银川模拟)如图，△A′B′C′是△ABC的直观图，其中A′B′＝A′C′，A′B′∥x′轴，A′C′∥y′轴，那么△ABC是(　　)‎ A．等腰三角形 B．钝角三角形 C．等腰直角三角形 D．直角三角形 ‎2．以下命题：①根据斜二测画法，三角形的直观图是三角形；②有两个平面互相平行，其余各面都是平行四边形的多面体是棱柱；③两相邻侧面所成角相等的棱锥是正棱锥；④若两个二面角的半平面互相垂直，则这两个二面角的大小相等或互补．其中正确命题的个数为(　　)‎ A．1 B．2 C．3 D．4‎ ‎3．已知长方体全部棱长的和为36，表面积为52，则其体对角线的长为(　　)‎ A．4 B. 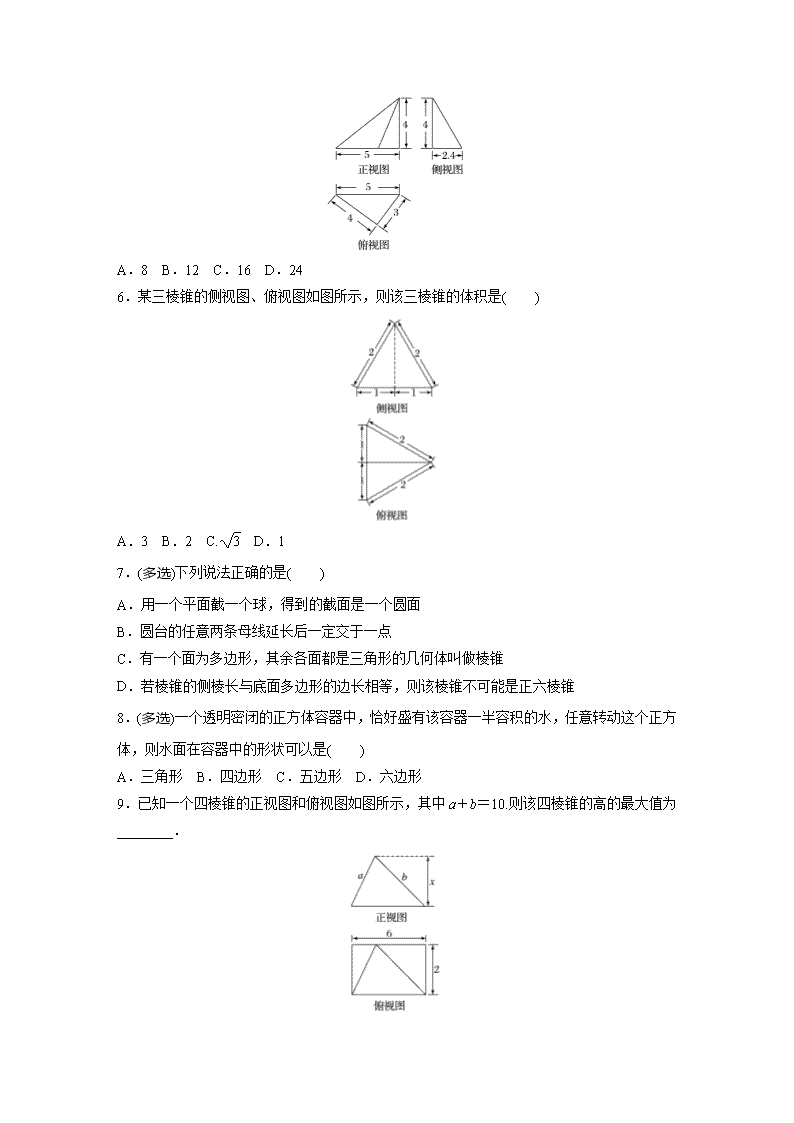C．2 D．4 ‎4．(2019·新疆沙雅县第二中学期末)如图是某几何体的三视图，则该几何体的体积是(　　)‎ A．9π＋42 B．36π＋18‎ C.π＋12 D.π＋18‎ ‎5．已知某几何体的三视图如图所示，则该几何体的体积为 A．8 B．12 C．16 D．24‎ ‎6．某三棱锥的侧视图、俯视图如图所示，则该三棱锥的体积是(　　)‎ A．3 B．2 C. D．1‎ ‎7．(多选)下列说法正确的是(　　)‎ A．用一个平面截一个球，得到的截面是一个圆面 B．圆台的任意两条母线延长后一定交于一点 C．有一个面为多边形，其余各面都是三角形的几何体叫做棱锥 D．若棱锥的侧棱长与底面多边形的边长相等，则该棱锥不可能是正六棱锥 ‎8．(多选)一个透明密闭的正方体容器中，恰好盛有该容器一半容积的水，任意转动这个正方体，则水面在容器中的形状可以是(　　)‎ A．三角形 B．四边形 C．五边形 D．六边形 ‎9．已知一个四棱锥的正视图和俯视图如图所示，其中a＋b＝10.则该四棱锥的高的最大值为________．‎ ‎10.如图，正方体ABCD－A1B1C1D1的棱长为2，动点P在对角线BD1上，过点P作垂直于 BD1的平面，记这样得到的截面多边形(含三角形)的周长为y，设BP＝x，则当x∈[1,5]时，函数y＝f(x)的值域为________．‎ ‎11.(2020·酒泉质检)如图，在长方体ABCD－A1B1C1D1中，AA1＝AB＝2，BC＝3，点P在线段B1D1上，的方向为正视方向，当AP最短时，棱锥P－AA1B1B的侧视图为(　　)‎ ‎12．已知三棱锥的三视图如图所示，则该三棱锥外接球的表面积为(　　)‎ A．4π B．16π C．18π D．36π ‎13.如图，棱长为2的正方体ABCD－A1B1C1D1中，E为CC1的中点，点P，Q分别为面A1B1C1D1和线段B1C上的动点，则△PEQ周长的最小值为(　　)‎ A．2 B. C. D．2 ‎14．在立体几何中，用一个平面去截一个几何体得到的平面图形叫截面. 如图，在棱长为1的正方体ABCD－A1B1C1D1中，点E，F分别是棱B1B，B1C1的中点，点G是棱CC1的中点，则过线段AG且平行于平面A1EF的截面的面积为(　　)‎ A．1 B. C. D. ‎15．已知一个几何体的三视图如图所示(单位：cm)，则该几何体的体积为________ cm3.‎ ‎16．一个四面体的三视图如图所示，则该四面体四个面当中最大面的面积是________．‎ 答案精析 ‎1．D　2.A　3.B　4.D　5.A　6.D ‎7．ABD　8.BD　9.4　10.[3，6]‎ ‎11．B　[在Rt△AA1P中，AP2＝AA＋A1P2，当AP最短时，A1P最短，即A1P⊥B1D1，AA1＝AB＝2，BC＝3，在△A1B1D1中通过长度关系知道P靠近B1，侧视图为B项的图形，故选B.]‎ ‎12．B　[根据三视图可知几何体是一个三棱锥，如图，‎ 底面是一个直角三角形，AC⊥BC，D是AB的中点，PD⊥平面ABC，且AC＝2，BC＝2，PD＝2，‎ ‎∴AB＝＝4，AD＝BD＝CD＝2，‎ ‎∴几何体的外接球的球心是D，则球的半径r＝2，‎ 即几何体的外接球表面积S＝4πr2＝16π，故选B.]‎ ‎13．B　[由题意得，△PEQ周长取最小值时，P在B1C1上，在平面B1C1CB上，设E关于B1C的对称点为M，关于B1C1的对称点为N，连接MN，‎ 当MN与B1C1的交点为P，MN与B1C的交点为Q时，‎ 则MN是△PEQ周长的最小值，‎ EM＝，EN＝2，∠MEN＝135°，‎ ‎∴MN＝＝.‎ ‎∴△PEQ周长的最小值为.故选B.]‎ ‎14．B　[取BC的中点H，连接AH，GH，‎ ‎∵EF∥BC1∥GH，EF⊄平面AHGD1，GH⊂平面AHGD1，‎ ‎∴EF∥平面AHGD1，‎ 同理，A1E∥平面AHGD1，‎ 又A1E∩EF＝E，则平面AHGD1∥平面A1EF，‎ 等腰梯形AHGD1的上、下底分别为，，‎ 腰长为，故梯形的高为，‎ 则梯形面积为.即截面的面积为.]‎ ‎15．36－ 解析　由三视图可知，题中所给的几何体是由一个长方体挖去一个圆锥形成的组合体，‎ 其中长方体的长、宽、高分别为3 cm，4 cm，3 cm，‎ 圆锥的底面半径为R＝ cm，圆锥的高h＝2 cm，‎ 故所求几何体的体积V＝3×4×3－××2＝36－(cm3)．‎ ‎16．2 解析　由三视图可知，该四面体为D－BD1C1，放在正方体中，由直观图可知，面积最大的面为△BDC1，在正三角形BDC1中，BD＝2，所以其面积S＝×(2)2×＝2.‎