2021高考数学新高考版一轮习题：专题7 第54练 平行与垂直小题练 Word版含解析 6页

‎1．(2020·辽宁省部分重点高中联考)把正方形ABCD沿对角线AC折起，当以A，B，C，D四点为顶点的三棱锥体积最大时，二面角B－AC－D的大小为(　　)‎ A．30° B．45° C．60° D．90°‎ ‎2．如图所示，已知平面CBD⊥平面ABD，且DA⊥平面ABC，则△ABC的形状为(　　)‎ A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定 ‎3．在Rt△ABC中，∠ABC＝90°，P为△ABC所在平面外一点，PA⊥平面ABC，则四面体P－ABC中直角三角形的个数为(　　)‎ A．4 B．3 C．2 D．1‎ ‎4．(2020·成都质检)如图所示，PA垂直于以AB为直径的圆O所在的平面，C为圆上异于A，B的任一点，则下列关系中不正确的是(　　)‎ A．PA⊥BC B．BC⊥平面PAC C．AC⊥PB D．PC⊥BC ‎5.如图所示，在斜三棱柱ABC－A1B1C1中，∠BAC＝90°，又BC1⊥AC，过C1作C1H⊥底面ABC，垂足为H，则点H一定在(　　)‎ A．直线AC上 B．直线AB上 C．直线BC上 D．△ABC的内部 ‎6．(2019·安徽省太和中学月考)如图，在四边形ABCD中，AD∥BC，AD＝AB，∠BCD＝45°，∠BAD＝90°，将△ABD沿BD折起，使平面ABD⊥平面BCD构成几何体A－BCD，则在几何体A－BCD中，下列结论正确的是(　　)‎ A．平面ADC⊥平面ABC B．平面ADC⊥平面BDC C．平面ABC⊥平面BDC D．平面ABD⊥平面ABC ‎7．(多选)如图，已知正方体ABCD－A1B1C1D1的棱长为2，E为棱CC1的中点，F为棱AA1上的点，且满足A1F∶FA＝1∶2，点F，B，E，G，H为过三点B，E，F的平面BMN与正方体ABCD－A1B1C1D1的棱的交点，则下列说法正确的是(　　)‎ A．HF∥BE B．三棱锥的体积＝4‎ C．直线MN与平面A1B1BA所成的角为45°‎ D．D1G∶GC1＝1∶3‎ ‎8．(多选)如图所示，在直角梯形BCEF中，∠CBF＝∠BCE＝90°，A，D分别是BF，CE上的点，AD∥BC，且AB＝DE＝2BC＝2AF(如图①)．将四边形ADEF沿AD折起，连接BE，BF，CE(如图②)．在折起的过程中，下列说法中正确的是(　　)‎ A．AC∥平面BEF B．B，C，E，F四点不可能共面 C．若EF⊥CF，则平面ADEF⊥平面ABCD D．平面BCE与平面BEF可能垂直 ‎9．如图所示，S是直角三角形ABC所在平面外一点，SA＝SB＝SC，点D为斜边AC的中点，则直线SD与平面ABC的位置关系为________．‎ ‎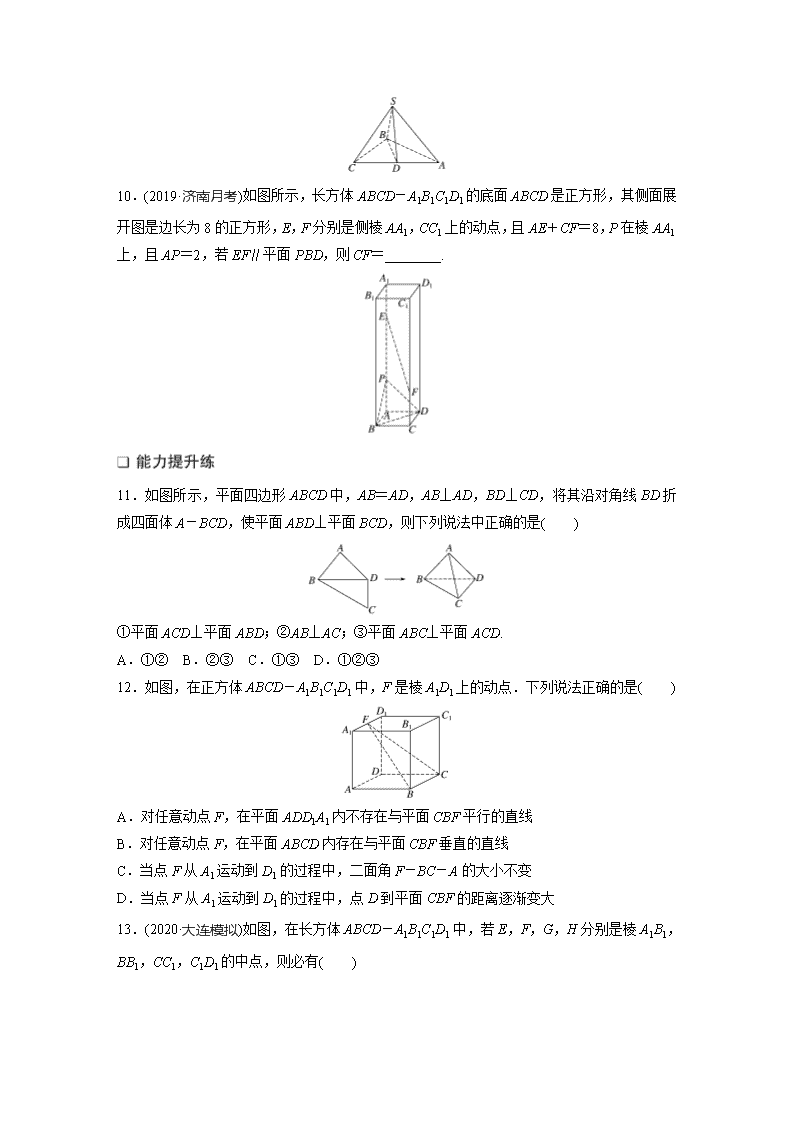10．(2019·济南月考)如图所示，长方体ABCD－A1B1C1D1的底面ABCD是正方形，其侧面展开图是边长为8的正方形，E，F分别是侧棱AA1，CC1上的动点，且AE＋CF＝8，P在棱AA1上，且AP＝2，若EF∥平面PBD，则CF＝________.‎ ‎11．如图所示，平面四边形ABCD中，AB＝AD，AB⊥AD，BD⊥CD，将其沿对角线BD折成四面体A－BCD，使平面ABD⊥平面BCD，则下列说法中正确的是(　　)‎ ‎①平面ACD⊥平面ABD；②AB⊥AC；③平面ABC⊥平面ACD.‎ A．①② B．②③ C．①③ D．①②③‎ ‎12．如图，在正方体ABCD－A1B1C1D1中，F是棱A1D1上的动点．下列说法正确的是(　　)‎ A．对任意动点F，在平面ADD1A1内不存在与平面CBF平行的直线 B．对任意动点F，在平面ABCD内存在与平面CBF垂直的直线 C．当点F从A1运动到D1的过程中，二面角F－BC－A的大小不变 D．当点F从A1运动到D1的过程中，点D到平面CBF的距离逐渐变大 ‎13．(2020·大连模拟)如图，在长方体ABCD－A1B1C1D1中，若E，F，G，H分别是棱A1B1，BB1，CC1，C1D1的中点，则必有(　　)‎ A．BD1∥GH B．BD∥EF C．平面EFGH∥平面ABCD D．平面EFGH∥平面A1BCD1‎ ‎14．(多选)在边长为2的正三角形ABC中，D，E，M分别是AB，AC，BC的中点，N为DE的中点，将△ADE沿DE折起至△A′DE的位置，使A′M＝.设MC的中点为Q，A′B的中点为P，下列说法中正确的有(　　)‎ A．A′N⊥平面BCED B．NQ∥平面A′EC C．DE⊥平面A′MN D．平面PMN∥平面A′EC ‎15．圆锥的顶点为P，它的轴截面是等腰直角三角形PAB，圆锥侧面积为π，点C是以AB为直径的圆O上的点，且BC＝.点E在线段PB上，则CE＋OE的最小值为________．‎ ‎16．(2019·安徽省皖中名校联盟联考)如图所示，在直角梯形ABCD中，BC⊥DC，AE⊥DC，M，N分别是AD，BE的中点，将△ADE沿AE折起，下列说法正确的是________(填上所有正确的序号)．‎ ‎①不论D折至何位置(不在平面ABC内)都有MN∥平面DEC；‎ ‎②不论D折至何位置都有MN⊥AE；‎ ‎③不论D折至何位置(不在平面ABC内)都有MN∥AB.‎ 答案精析 ‎1．D　2.B　3.A　4.C　5.B　6.A ‎7．ABD　8.ABC　9.垂直　10.2　11.D　12.C ‎13．D　[选项A，由中位线定理可知GH∥D1C，因为过直线外一点有且只有一条直线与已知直线平行，所以BD1，GH不可能互相平行，故A选项是错误的；选项B，由中位线定理可知EF∥A1B，因为过直线外一点有且只有一条直线与已知直线平行，所以BD，EF不可能互相平行，故B选项是错误的；选项C，由中位线定理可知EF∥A1B，而直线A1B与平面ABCD相交，故直线EF与平面ABCD也相交，故平面EFGH与平面ABCD相交，故C选项是错误的；选项D，由三角形中位线定理可知EF∥A1B，EH∥A1D1，所以有EF∥平面A1BCD1，EH∥平面A1BCD1，而EF∩EH＝E，因此平面EFGH∥平面A1BCD1，故选D.]‎ ‎14．ABC　[结合题意画出图形如图所示．‎ 对于A，由题意可得A′N＝NM＝，‎ 又A′M＝，所以A′N2＋NM2＝A′M2，‎ 从而得到∠A′NM＝90°，故得A′N⊥NM，‎ 又A′N⊥ED，ED∩NM＝N，ED，NM⊂平面BCED，‎ 所以A′N⊥平面BCED，所以A正确；‎ 对于B，因为N为DE的中点，Q为MC的中点，DE∥BC，DE＝BC，‎ 所以EN∥CQ，EN＝CQ，‎ 所以四边形ENQC为平行四边形，所以CE∥NQ，‎ 因为NQ⊄平面A′EC，CE⊂平面A′EC，所以NQ∥平面A′EC，所以B正确；‎ 对于C，由题意可得DE⊥A′N，DE⊥MN，‎ 又A′N∩MN＝N，A′N，MN⊂平面A′MN，所以DE⊥平面A′MN，所以C正确；‎ 对于D，由题意可知MN与CE在同一平面内且不平行，‎ 所以MN与CE一定有交点，即平面PMN与平面A′EC有交线，所以D不正确．‎ 综上可得ABC正确．故选ABC.]‎ ‎15. 解析　设圆O的直径为2r，则半径为r，‎ 圆锥的母线长为l，‎ 又它的轴截面是等腰直角三角形，‎ ‎∴S侧＝πrl＝π·r·r＝π，得r＝1，‎ 则l＝PA＝，PO＝1，‎ 当E为PB的中点时，由OB＝OP＝1，‎ 得OE⊥PB，OE＝，‎ 由CP＝BC＝，得CE⊥PB，CE＝，‎ ‎∴由题意得当E为PB的中点时，CE＋OE最小，‎ 最小值为.‎ ‎16．①②‎ 解析　①在直角梯形ABCD中，由BC⊥DC，AE⊥DC，知四边形ABCE为矩形．‎ 连接AC，∵N为BE的中点，则AC过点N.‎ 当D折至某一位置时，如图所示，‎ 连接MN，∵M为AD的中点，N为AC的中点，‎ ‎∴MN为△ADC的中位线，∴MN∥CD，‎ ‎∵MN⊄平面DEC，CD⊂平面DEC，‎ ‎∴MN∥平面DEC，①正确；‎ ‎②由已知，AE⊥ED，AE⊥EC，ED∩EC＝E，‎ ‎∴AE⊥平面DEC，CD⊂平面DEC，‎ ‎∴AE⊥CD，∴MN⊥AE，②正确；‎ ‎③MN与AB异面，假设MN∥AB，‎ 由MN∥DC知，DC∥AB，‎ 又CE∥AB，得CE∥DC，‎ 这与CE∩CD＝C相矛盾，∴假设不成立，③错误．‎