- 164.00 KB
- 2021-06-30 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第三章检测试题
时间:90分钟 分值:120分
第Ⅰ卷(选择题,共60分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若a<0,-1ab>ab2 B.ab2>ab>a
C.ab>a>ab2 D.ab>ab2>a
解析:由-1b2>0>b,由a<0,得ab>ab2>a.
2.若<<0,则下列结论正确的是( A )
A.a>b B.abb2
解析:因为<<0,所以b4或x<-1}
C.{x|x>1或x<-4}
D.{x|-40,即(x+1)(x-4)>0,解得x>4或x<-1.故不等式的解集为{x|x>4或x<-1}.
5.若关于x的不等式x2+px+q<0的解集为{x|10的解集是( D )
A.(1,2)
B.(-∞,-1)∪(6,+∞)
C.(-1,1)∪(2,6)
D.(-∞,-1)∪(1,2)∪(6,+∞)
解析:由题知x2+px+q=(x-1)(x-2),
7
故>0,
同解于(x-1)(x-2)(x+1)(x-6)>0,
得x<-1,或16.故选D.
6.若正实数x,y满足x+y=2,且≥M恒成立,则M的最大值为( A )
A.1 B.2
C.3 D.4
解析:因为x+y≥2,且x+y=2,
所以2≥2,当且仅当x=y=1时,等号成立,
所以xy≤1,所以≥1,
所以1≥M,所以Mmax=1.故选A.
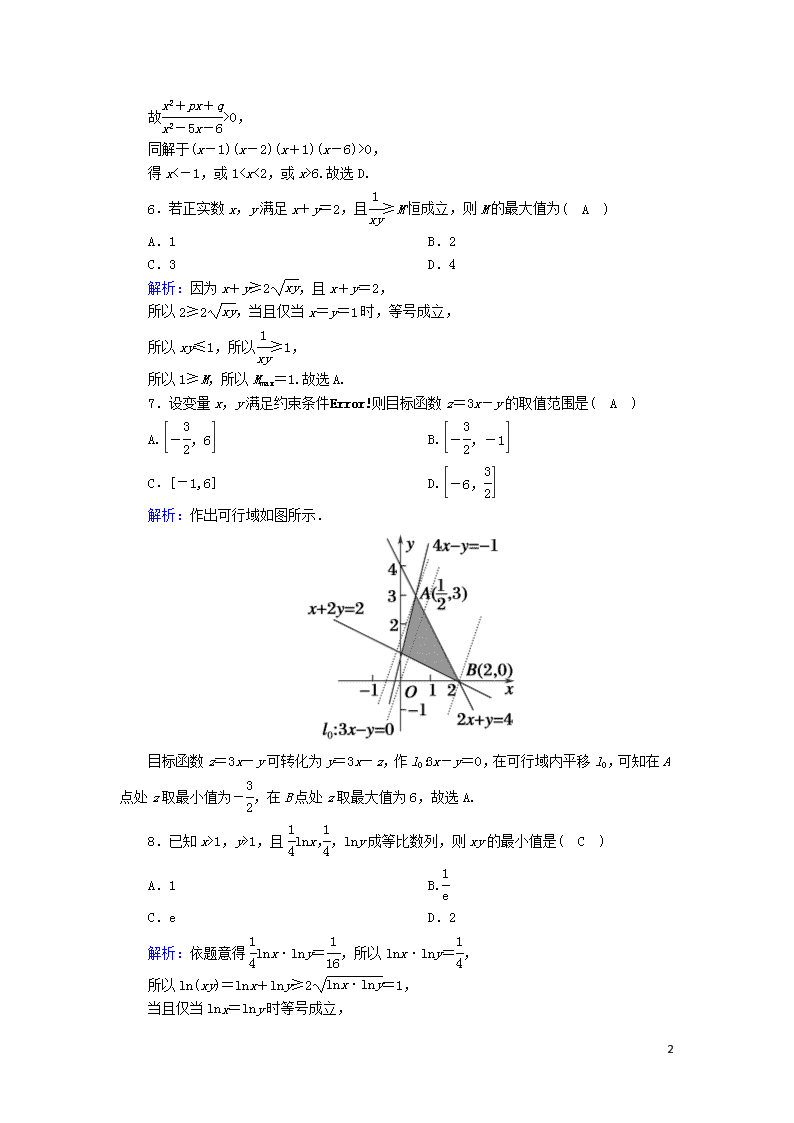
7.设变量x,y满足约束条件则目标函数z=3x-y的取值范围是( A )
A. B.
C.[-1,6] D.
解析:作出可行域如图所示.
目标函数z=3x-y可转化为y=3x-z,作l0:3x-y=0,在可行域内平移l0,可知在A点处z取最小值为-,在B点处z取最大值为6,故选A.
8.已知x>1,y>1,且lnx,,lny成等比数列,则xy的最小值是( C )
A.1 B.
C.e D.2
解析:依题意得lnx·lny=,所以lnx·lny=,
所以ln(xy)=lnx+lny≥2=1,
当且仅当lnx=lny时等号成立,
所以xy≥e,所以xy的最小值是e.故选C.
7
9.在平面直角坐标系中,不等式组(a为常数)表示平面区域的面积为9,则的最小值为( D )
A.-1 B.
C. D.-
解析:不等式组表示的可行域如图阴影部分所示.
则×a×2a=9,a=3,
则A(3,-3),点(-4,2)与点(x,y)的连线的斜率为,当点(x,y)为(3,-3)时,最小,最小值为-.
故选D.
10.当x>0时,x2+mx+4≥0恒成立,且关于t的不等式t2+2t+m≤0有解,则实数m的取值范围是( B )
A.[1,+∞)
B.[-4,1]
C.(-∞,-4]∪[1,+∞)
D.(-∞,-4]
解析:∵当x>0时,x2+mx+4≥0恒成立,
∴m≥-.
∵x+≥2=4,当且仅当x=2时取等号,
∴m≥-4.
∵关于t的不等式t2+2t+m≤0有解,
∴Δ=4-4m≥0,∴m≤1.
故实数m的取值范围是[-4,1].故选B.
11.已知a>b>1,P=,Q=(lga+lgb),R=lg,则P,Q,R的关系是( D )
A.P>Q>R B.Q>R>P
C.P>R>Q D.R>Q>P
7
解析:因为a>b>1,所以lga>0,lgb>0,
<=
=lg-2},求k的值;
(2)若不等式的解集是R,求k的取值范围.
解:(1)因为不等式的解集为{x|x<-3或x>-2},所以-3,-2是方程kx2-2x+6k=0的两根且k<0.
由根与系数的关系得
解得k=-.
(2)因为不等式的解集为R,
所以
即
所以k<-.
即k的取值范围是.
18.(10分)电视台与某广告公司签约播放两部影片集,其中影片集甲每集播放时间为19分钟(不含广告时间,下同),广告时间为1分钟,收视观众为60万;影片集乙每集播放时间为7分钟,广告时间为1分钟,收视观众为20万,广告公司规定每周至少有6分钟广告,而电视台每周只能为该公司提供不多于80分钟的节目时间(含广告时间).
(1)问电视台每周应播放两部影片集各多少集,才能使收视观众最多.
(2)在获得最多收视观众的情况下,影片集甲、乙每集可分别给广告公司带来a和b(万元)的效益,若广告公司本周共获得3万元的效益,记S=+
7
为效益调和指数(单位:万元),求效益调和指数的最小值.
解:(1)设影片集甲乙分别播放x,y集,
由题意得
要使收视观众最多,只要z=60x+20y最大即可.
作出可行域,如图,
由解得A,
所以满足题意的最优解为(2,5),
zmax=60×2+20×5=220,故电视台每周影片集甲播出2集,影片集乙播出5集,能使收视观众最多.
(2)由题意得:2a+5b=3,则
S=+=(2a+5b)=≥27,
当且仅当a=,b=时取等号,所以效益调和指数的最小值为27万元.
19.(10分)设集合A为函数y=ln(-x2-2x+8)的定义域,集合B为函数y=x+的值域,集合C为不等式(x+4)≤0的解集.
(1)求A∩B.
(2)若C⊆∁RA,求a的取值范围.
解:(1)因为-x2-2x+8>0,
可以解得A=(-4,2).
因为y=x+,
所以B=(-∞,-3]∪[1,+∞).
所以A∩B=(-4,-3]∪[1,2).
(2)因为∁RA=(-∞,-4]∪[2,+∞),C⊆∁RA,
若a<0,则不等式(x+4)≤0的解集只能是(-∞,-4]∪,故一定有≥2,得a2≤,解得-≤a<0;
7
若a>0,则不等式(x+4)≤0的解集是,但C⊆∁RA,故a∈∅,所以a的范围为-≤a<0.
20.(10分)已知函数f(x)=x2-2ax-1+a,a∈R.
(1)若a=2,试求函数y=(x>0)的最小值;
(2)对于任意的x∈[0,2],不等式f(x)≤a成立,试求a的取值范围.
解:(1)依题意得y===x+-4.
因为x>0,所以x+≥2.
当且仅当x=,即x=1时,等号成立.
所以y≥-2.
故当x=1时,y=的最小值为-2.
(2)因为f(x)-a=x2-2ax-1,所以要使得“任意的x∈[0,2],不等式f(x)≤a成立”,只要“x2-2ax-1≤0在[0,2]上恒成立”.不妨设g(x)=x2-2ax-1,
则只要g(x)≤0在[0,2]上恒成立.
所以
即
解得a≥.
所以a的取值范围是.
7
相关文档
- 高考数学专题复习练习第六章 第四2021-06-305页
- 2021高考数学一轮复习课后限时集训2021-06-303页
- 2018届二轮复习 坐标系与参数方程2021-06-301页
- 高考数学专题复习课件: 第一节 绝2021-06-3041页
- 2020届艺术生高考数学二轮复习课时2021-06-304页
- 2018届二轮复习不等式选讲课件2021-06-3017页
- 2019届二轮复习(理)不等式选讲学案(全2021-06-3017页
- 【数学】2020届一轮复习(文理合用)第2021-06-306页
- 高考文科数学复习备课课件:第四节 2021-06-3026页
- 高考数学专题复习教案: 基本不等式2021-06-302页