高考数学专题复习：概率与统计精选精练初稿答案 5页

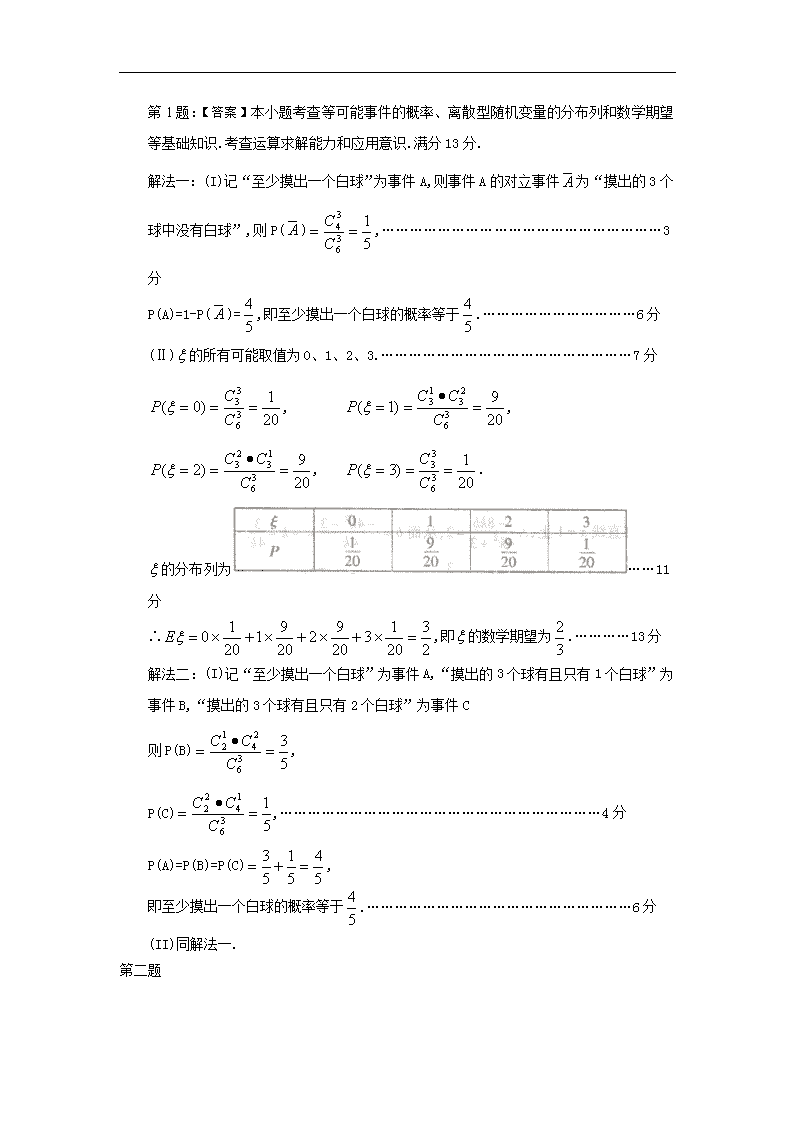
第1题：【答案】本小题考查等可能事件的概率、离散型随机变量的分布列和数学期望等基础知识.考查运算求解能力和应用意识.满分13分.‎ 解法一：(I)记“至少摸出一个白球”为事件A,则事件A的对立事件为“摸出的3个球中没有白球”,则P(),……………………………………………………3分 P(A)=1-P()=,即至少摸出一个白球的概率等于.……………………………6分 ‎(Ⅱ)的所有可能取值为O、1、2、3.………………………………………………7分 ‎, ,‎ ‎, .‎ 的分布列为……11分 ‎∴,即的数学期望为.…………13分 解法二：(I)记“至少摸出一个白球”为事件A,“摸出的3个球有且只有1个白球”为事件B,“摸出的3个球有且只有2个白球”为事件C 则P(B),‎ P(C),……………………………………………………………4分 P(A)=P(B)=P(C),‎ 即至少摸出一个白球的概率等于.…………………………………………………6分 ‎(II)同解法一.‎ 第二题 解：设事件A为：“方程有实根”.‎ 当时，方程有实根得充要条件为.‎ ‎（1）基本事件共12个：‎ 其中第一个数表示的取值，第二个数表示的取值.‎ 事件A包含9个基本事件，事件A发生的概率为.‎ ‎（2）实验的全部结果所构成的区域为.‎ 构成事件A的区域为 所以所求的概率为.‎ 第4题：‎ ‎【答案】本题主要考查随机事件、互斥事件、相互独立事件等概率知识、考查离散型随机变量的分布列和期望等基础知识，考查运用概率与统计知识解决实际问题的能力.‎ ‎（Ⅰ）设这名学生在上学路上到第三个路口时首次遇到红灯为事件A，因为事件A等于事件“这名学生在第一和第二个路口没有遇到红灯，在第三个路口遇到红灯”‎ ‎，所以事件A的概率为.‎ ‎（Ⅱ）由题意，可得可能取的值为0，2，4，6，8（单位：min）.‎ 事件“”等价于事件“该学生在路上遇到次红灯”（0，1，2，3，4），‎ ‎∴，‎ ‎∴即的分布列是 ‎0‎ ‎2‎ ‎4‎ ‎6‎ ‎8‎ ‎∴的期望是.‎ 第5题：‎ ‎【答案】本小题主要考查概率统计的基础知识，考查推理论证能力、数据处理能力、运算求解能力及应用意识，考查或然与必然的思想，满分13分．‎ ‎（Ⅰ）， 2分 因线性回归方程过点，‎ ‎∴， 4分 ‎∴6月份的生产甲胶囊的产量数：. 6分 ‎（Ⅱ）‎ ‎ 11分 其分布列为 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎ 13分 第6题：‎ ‎【答案】解：（1）由图得，成绩在的人数为4人，‎ 所以在的人为16人，‎ 所以在的频率为，‎ 在的频率为．………2分 补全的 ‎ ‎（2）由题得：成绩在的有8人，‎ 在的为16人．‎ 所以的概率为．………6分 ‎（3） 的分布列为:‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎ ……………9分 随机变量服从的是M=50,N=20,n=4的超几何分布，所以期望．…………12分 第7题：‎ ‎【答案】解：（Ⅰ）众数：4.6和4.7；中位数：4.75 …………………………2分 ‎（Ⅱ）设表示所取3人中有个人是“好视力”，至多有1人是“好视力”记为事件，则 ……………6分 ‎（Ⅲ）的可能取值为0、1、2、3 …………………7分 ‎ ‎ 分布列为 ‎ ………………………10分 ‎. ……………………12分 第8题：‎ ‎【答案】本小题主要考查频率分布直方表、随机变量的分布列、数学期望等基础知识，考查数据处理能力、运算求解能力以及应用用意识，考查必然与或然思想等．解：(Ⅰ) 众数为22.5微克/立方米, 中位数为37.5微克/立方米．………………4分 ‎（Ⅱ）去年该居民区PM2.5年平均浓度为 ‎（微克/立方米）．…………………6分 因为，所以去年该居民区PM2.5年平均浓度不符合环境空气质量标准，‎ 故该居民区的环境需要改进．……………………………………………8分 ‎（Ⅲ）记事件A表示“一天PM2.5的24小时平均浓度符合环境空气质量标准”，则.………………9分 随机变量的可能取值为0,1,2.且.‎ 所以，…………………………………………11分 所以变量的分布列为 ‎0‎ ‎1‎ ‎2‎ ‎…………………………………………12分 ‎（天）,或（天）. ………13分