高中物理人教版必修2练习：第六章 第6讲 习题课：天体运动 word版含解析 8页

第 6 讲 习题课：天体 运动 [时间：60 分钟] 题组一 天体运动规律的理解及应用 1.(2015·山东理综·15)如图 1 所示，拉格朗日点 L1 位于地球和月球连线上，处在该点的物体在 地球和月球引力的共同作用下，可与月球一起以相同的周期绕地球运动．据此，科学家设想 在拉格朗日点 L1 建立空间站，使其与月球同周期绕地球运动．以 a1、a2 分别表示该空间站和 月球向心加速度的大小，a3 表示地球同步卫星向心加速度的大小．以下判断正确的是( ) 图 1 A．a2>a3>a1 B．a2>a1>a3 C．a3>a1>a2 D．a3>a2>a1 2．据观测，某行星外围有一模糊不清的环，为了判断该环是连续物还是卫星群，又测出了环 中各层的线速度 v 的大小与该层至行星中心的距离 R，则以下判断中正确的是( ) A．若 v 与 R 成正比，则环是连续物 B．若 v 与 R 成反比，则环是连续物 C．若 v2 与 R 成正比，则环是卫星群 D．若 v2 与 R 成反比，则环是卫星群 3．土星的卫星众多，其中土卫五和土卫六的半径之比为R5 R6 ，质量之比为m5 m6 ，围绕土星做圆周 运动的半径之比为r5 r6 ，下列判断正确的是( ) A．土卫五和土卫六的公转周期之比为 r5 r6 3 2 B．土星对土卫五和土卫六的万有引力之比为 m6 m5 r6 r5 2 C．土卫五和土卫六的公转速度之比为 r6 r5 2 1 D．土卫五和土卫六表面的重力加速度之比为 m5 m6 R6 R5 2 题组二 “赤道上的物体”与“同步卫星”以及“近地卫星”的区别 4．关于近地卫星、同步卫星、赤道上的物体，以下说法正确的是( ) A．都是万有引力等于向心力 B．赤道上的物体和同步卫星的周期、线速度、角速度都相等 C．赤道上的物体和近地卫星的轨道半径相同但线速度、周期不同 D．同步卫星的周期大于近地卫星的周期 5．设地球半径为 R，a 为静止在地球赤道上的一个物体，b 为一颗近地绕地球做匀速圆周运动 的人造卫星，c 为地球的一颗同步卫星，其轨道半径为 r.下列说法中正确的是( ) A．a 与 c 的线速度大小之比为 r R B．a 与 c 的线速度大小之比为 R r C．b 与 c 的周期之比为 r R D．b 与 c 的周期之比R r R r 6．我国发射的“北斗系列”卫星中同步卫星到地心距离为 r，运行速率为 v1，向心加速度为 a1；在地球赤道上的观测站的向心加速度为 a2，近地卫星做圆周运动的速率为 v2，向心加速度 为 a3，地球的半径为 R，则下列比值正确的是( ) A.a1 a2 ＝r R B.a2 a3 ＝R3 r3 C.v1 v2 ＝r R D.a1 a2 ＝R2 r2 题组三 卫星、飞船的发射和变轨问题 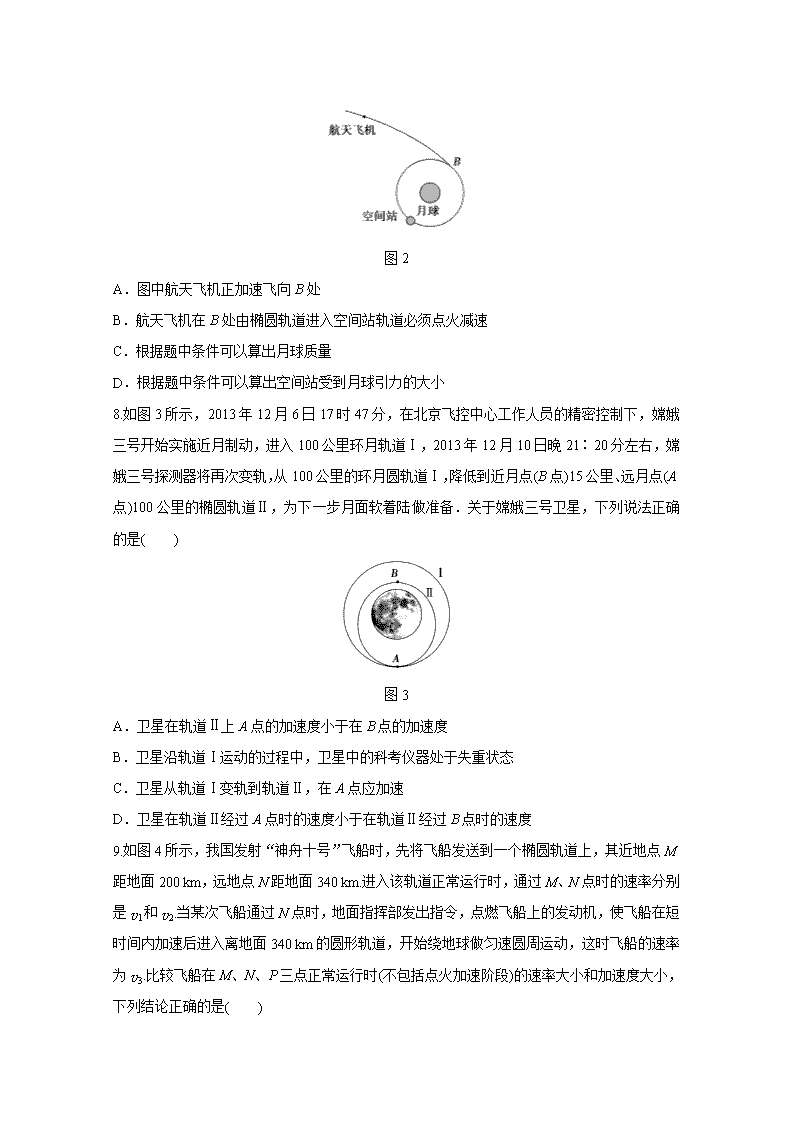7.未来将建立月球基地，并在绕月轨道上建造空间站．如图 2 所示，关闭动力的航天飞机在月 球引力作用下向月球靠近，并将与空间站在 B 处对接，已知空间站绕月轨道半径为 r，周期为 T，万有引力常量为 G，下列说法中正确的是( ) 图 2 A．图中航天飞机正加速飞向 B 处 B．航天飞机在 B 处由椭圆轨道进入空间站轨道必须点火减速 C．根据题中条件可以算出月球质量 D．根据题中条件可以算出空间站受到月球引力的大小 8.如图 3 所示，2013 年 12 月 6 日 17 时 47 分，在北京飞控中心工作人员的精密控制下，嫦娥 三号开始实施近月制动，进入 100 公里环月轨道Ⅰ，2013 年 12 月 10 日晚 21∶20 分左右，嫦 娥三号探测器将再次变轨，从 100 公里的环月圆轨道Ⅰ，降低到近月点(B 点)15 公里、远月点 (A 点)100 公里的椭圆轨道Ⅱ，为下一步月面软着陆做准备．关于嫦娥三号卫星，下列说法正 确的是( ) 图 3 A．卫星在轨道Ⅱ上 A 点的加速度小于在 B 点的加速度 B．卫星沿轨道Ⅰ运动的过程中，卫星中的科考仪器处于失重状态 C．卫星从轨道Ⅰ变轨到轨道Ⅱ，在 A 点应加速 D．卫星在轨道Ⅱ经过 A 点时的速度小于在轨道Ⅱ经过 B 点时的速度 9.如图 4 所示，我国发射“神舟十号”飞船时，先将飞船发送到一个椭圆轨道上，其近地点 M 距地面 200 km，远地点 N 距地面 340 km.进入该轨道正常运行时，通过 M、N 点时的速率分别 是 v1 和 v2.当某次飞船通过 N 点时，地面指挥部发出指令，点燃飞船上的发动机，使飞船在短 时间内加速后进入离地面 340 km 的圆形轨道，开始绕地球做匀速圆周运动，这时飞船的速率 为 v3.比较飞船在 M、N、P 三点正常运行时(不包括点火加速阶段)的速率大小和加速度大小， 下列结论正确的是( ) 图 4 A．v1>v3>v2，a1>a3>a2 B．v1>v2>v3，a1>a2＝a3 C．v1>v2＝v3，a1>a2>a3 D．v1>v3>v2，a1>a2＝a3 题组四 双星及三星问题 10．宇宙中有两颗星球组成的双星，在相互之间的万有引力作用下绕连线上的某点做周期相 同的匀速圆周运动．现测得两颗星球之间的距离为 L，质量之比为 m1∶m2＝3∶2，则下列说 法正确的是( ) A．m1、m2 做圆周运动的线速度之比是 3∶2 B．m1、m2 做圆周运动的角速度之比是 3∶2 C．m1 做圆周运动的半径为 2 5L D．m2 做圆周运动的半径为 2 5L 11.宇宙中存在一些离其他恒星较远的、由质量相等的三颗星组成的三星系统，通常可忽略其 他星体对它们的引力作用，已观测到稳定的三星系统存在形式之一是：如图 5 所示，三颗星 位于同一直线上，两颗环绕星围绕中央星在同一半径为 R 的圆形轨道上运行，设每个星体的 质量均为 M，则( ) 图 5 A．环绕星运动的线速度为 GM R B．环绕星运动的角速度为 5GM 4R C．环绕星运动的周期为 T＝4π R3 5GM D．环绕星运动的周期为 T＝2π R3 GM 题组五 综合应用 12.如图 6，质量分别为 m 和 M 的两个星球 A 和 B 在引力作用下都绕 O 点做匀速圆周运动， 星球 A 和 B 两者中心之间的距离为 L.已知 A、B 的中心和 O 三点始终共线，A 和 B 分别在 O 的两侧．引力常量为 G. 图 6 (1)求两星球做圆周运动的周期； (2)在地月系统中，若忽略其他星球的影响，可以将月球和地球看成上述星球 A 和 B，月球绕 其轨道中心运行的周期记为 T1.但在近似处理问题时，常常认为月球是绕地心做圆周运动的， 这样算得的运行周期记为 T2.已知地球和月球的质量分别为 5.98×1024 kg 和 7.35×1022 kg.求 T2 与 T1 两者平方之比．(结果保留 3 位小数) 答案精析 第 6 讲 习题课：天体运动 1．D [因空间站建在拉格朗日点，故其周期等于月球的周期，根据 a＝4π2 T2 r 可知，a2>a1，对 空间站和地球的同步卫星而言，由于同步卫星的轨道半径较空间站的小，根据 a＝GM r2 可知 a3>a2，故选项 D 正确．] 2．AD [当环是连续物时，环上各点的角速度ω相同，v＝ωR，v 与 R 成正比，A 正确，B 错 误；当环是卫星群时，GMm R2 ＝mv2 R ，v＝ GM R ，v2＝GM R ，v2 与 R 成反比，故 C 错误，D 正确．] 3．ACD [根据公式 GMm r2 ＝m4π2 T2 r 得 T＝ 4π2r3 GM ，所以T5 T6 ＝ r 35 r 36 ＝ r5 r6 3 2 ，A 正确；根据公式 F＝G Mm r2 可得F5 F6 ＝m 5r 26 m6r 25 ，B 错误；由公式 GMm r2 ＝m v2 r 得 v＝ GM r ，所以v5 v6 ＝ r6 r5 ＝ r6 r5 2 1 ，C 正确；根据黄金代换公式 gR2＝Gm 可得 g＝Gm R2 ，所以g5 g6 ＝m5R 26 m6R 25 ，D 正确．] 4．CD [赤道上的物体是由万有引力的一个分力提供向心力，A 项错误；赤道上的物体和同 步卫星有相同周期和角速度，但线速度不同，B 项错误；同步卫星和近地卫星有相同的中心天 体，根据GMm r2 ＝mv2 r ＝m4π2 T2 r 得 v＝ GM r ，T＝2π r3 GM ，由于 r 同>r 近，故 v 同T 近， D 正确；赤道上物体、近地卫星、同步卫星三者间的周期关系为 T 赤＝T 同>T 近，根据 v＝ωr 可 知 v 赤mv2 r ，因此卫星做近心运动，而在Ⅰ轨道上的 A 点，由于 GMm r2 ＝mv′2 r ，因此 v′>v，故卫星从轨道Ⅰ变轨到轨道Ⅱ，应在 A 点减速，C 错误； 从 A 到 B 的过程中，由开普勒第二定律得在Ⅱ上 B 点的速度大于Ⅱ上 A 点的速度，D 正确．] 9．D [根据万有引力提供向心力，即GMm r2 ＝ma 得：a＝GM r2 ，由图可知 r1＜r2＝r3，所以 a1 ＞a2＝a3； 当某次飞船通过 N 点时，地面指挥部发出指令，点燃飞船上的发动机，使飞船在短时间内加 速后进入离地面 340 km 的圆形轨道，所以 v3＞v2，根据GMm r2 ＝mv2 r 得 v＝ GM r 又因为 r1＜r3， 所以 v1＞v3 故 v1＞v3＞v2.故选 D.] 10．C [两颗星球的角速度相等，B 错误；根据Gm1m2 L2 ＝m1ω2r1＝m2ω2r2，r1＋r2＝L 得，r1＝2 5L， r2＝3 5L，C 正确，D 错误；由 v＝ωr 知v1 v2 ＝r1 r2 ＝2 3 ，A 错误．] 11．C [对于某一个环绕星而言，受到两个星的万有引力，两个万有引力的合力提供环绕星做 圆周运动的向心力． 对某一个环绕星：GM2 R2 ＋GM2 4R2 ＝Mv2 R ＝MRω2＝MR4π2 T2 得 v＝ 5GM 4R ，ω＝ 5GM 4R3 ，T＝4π R3 5GM.故 C 正确．] 12．(1)2π L3 GM＋m (2)1.012 解析 (1)设两个星球 A 和 B 做匀速圆周运动的轨道半径分别为 r 和 R，相互作用的引力大小 为 F，运行周期为 T.根据万有引力定律有 F＝G mM R＋r2 ① 由匀速圆周运动的规律得 F＝m4π2 T2 r② F＝M4π2 T2 R③ 由题意得 L＝R＋r④ 联立①②③④式得 T＝2π L3 GM＋m.⑤ (2)在地月系统中，由于地月系统旋转所围绕的中心 O 不在地心，月球做圆周运动的周期可由 ⑤式得出 T1＝2π L′3 GM′＋m′ ⑥ 式中，M′和 m′分别是地球与月球的质量，L′是地心与月心之间的距离．若认为月球在地 球的引力作用下绕地心做匀速圆周运动，则 GM′m′ L′2 ＝m′4π2 T2 L′⑦ 式中，T2 为月球绕地心运动的周期．由⑦式得 T2＝2π L′3 GM′ ⑧ 由⑥⑧式得 T2 T1 2＝1＋m′ M′ 代入题给数据得T 22 T 21 ＝1.012.