高考文科数学复习备课课件：第三节　函数的奇偶性与周期性 30页

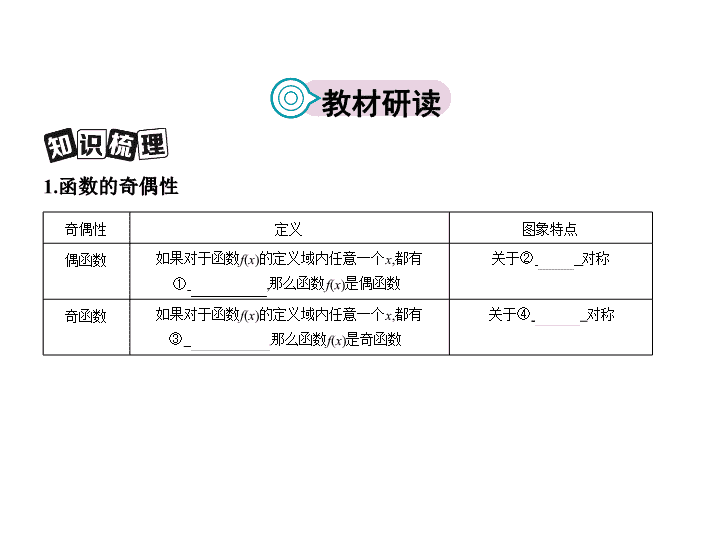
文数 课标版 第三节　函数的奇偶性与周期性 1.函数的奇偶性 教材研读 奇偶性 定义 图象特点 偶函数 如果对于函数 f ( x )的定义域内任意一个 x ,都有 ①      f (- x )= f ( x )     ,那么函数 f ( x )是偶函数 关于②      y 轴     对称 奇函数 如果对于函数 f ( x )的定义域内任意一个 x ,都有 ③      f (- x )=- f ( x )     ,那么函数 f ( x )是奇函数 关于④ 　原点     对称 2.奇(偶)函数的性质 (1)奇(偶)函数的定义域关于原点对称. (2)奇函数在关于原点对称的区间上的单调性⑤ 　相同     ,偶函数在关 于原点对称的区间上的单调性⑥ 　相反     . (3)在公共定义域内 (i)两个奇函数的和是⑦ 　奇函数     ,两个奇函数的积是⑧ 　偶函数     . (ii)两个偶函数的和、积都是⑨ 　偶函数     . (iii)一个奇函数,一个偶函数的积是⑩ 　奇函数     . (4)若函数 f ( x )是奇函数且在 x =0处有定义,则 f (0)=0. 3.周期性 (1)周期函数:对于函数 y = f ( x ),如果存在一个非零常数 T ,使得当 x 取定义 域内的任何值时,都有 f ( x + T )=        f ( x )     ,那么就称函数 y = f ( x )为周期函 数,称 T 为这个函数的周期. (2)最小正周期:如果在周期函数 f ( x )的所有周期中   　存在一个最小     的正数,那么这个最小正数就叫做 f ( x )的最小正周期.   　　判断下列结论的正误(正确的打“√”,错误的打“ × ”) (1)若 f ( x )是定义在R上的奇函数,则 f (- x )+ f ( x )=0.   (√) (2)偶函数的图象不一定过原点,奇函数的图象一定过原点.( × ) (3)如果函数 f ( x ), g ( x )为定义域相同的偶函数,则 F ( x )= f ( x )+ g ( x )是偶函数.   (√) (4)定义域关于原点对称是函数具有奇偶性的一个必要条件.(√) (5)若 T 是函数的一个周期,则 nT ( n ∈Z, n ≠ 0)也是函数的周期.   (√) (6)函数 f ( x )在定义域上满足 f ( x + a )=- f ( x ),则 f ( x )是周期为2 a ( a >0)的周期函 数.   (√)   1.(2015北京,3,5分)下列函数中为偶函数的是   (　　) A. y = x 2 sin x 　    B. y = x 2 cos x 　     C. y =|ln x |　    D. y =2 - x 答案     B    A中函数为奇函数,B中函数为偶函数,C与D中函数均为非奇 非偶函数,故选B. 2.(2015福建,3,5分)下列函数为奇函数的是   (　　) A. y =   　    B. y =e x 　    C. y =cos x 　    D. y =e x -e - x 答案     D    A、B选项中的函数为非奇非偶函数;C选项中的函数为偶函 数;D选项中的函数为奇函数,故选D. 3.(2014课标Ⅰ,5,5分)设函数 f ( x ), g ( x )的定义域都为R,且 f ( x )是奇函数, g ( x )是偶函数,则下列结论中正确的是   (　　) A. f ( x ) g ( x )是偶函数　    B. | f ( x )| g ( x )是奇函数 C. f ( x )| g ( x )|是奇函数　    D. | f ( x ) g ( x )|是奇函数 答案     C　由题意可知 f (- x )=- f ( x ), g (- x )= g ( x ),对于选项A, f (- x )· g (- x )=- f ( x )· g ( x ),所以 f ( x ) g ( x )是奇函数,故A项错误;对于选项B,| f (- x )| g (- x )=|- f ( x )| g ( x )=| f ( x )| g ( x ),所以| f ( x )| g ( x )是偶函数,故B项错误;对于选项C, f (- x )| g (- x )|=- f ( x )| g ( x )|,所以 f ( x )| g ( x )|是奇函数,故C项正确;对于选项D,| f (- x ) g (- x )|=|- f ( x ) g ( x )| =| f ( x ) g ( x )|,所以| f ( x ) g ( x )|是偶函数,故D项错误,选C. 4.已知定义在R上的奇函数 f ( x )满足 f ( x +4)= f ( x ),则 f (8)的值为   (　　) A.-1　    B.0　     C.1　    D.2 答案     B　∵ f ( x )为定义在R上的奇函数,且 f ( x +4)= f ( x ),∴ f (0)=0, T =4,∴ f (8)= f (0)=0. 5.若函数 f ( x )= ax 2 + bx +3 a + b 是偶函数,定义域为[ a -1,2 a ],则 a = 　　　     , b = 　　　     . 答案        ;0 解析 　因为偶函数的定义域关于原点对称,所以 a -1=-2 a ,解得 a =   . 由函数 f ( x )=   x 2 + bx + b +1为偶函数,结合偶函数图象的特点(图略),易得 b = 0. 考点一　函数奇偶性的判断与应用 典例1 　(1)下列函数:① f ( x )=   +   ;② f ( x )= x 3 - x ;③ f ( x )=ln( x +   );④ f ( x )=ln   ;⑤ f ( x )=( x +1)·   ;⑥ f ( x )=   ;⑦ f ( x )=   其中奇函数的个数是   (　　) A.3　    B.4　    C.5　    D.6 (2)(2015课标Ⅰ,13,5分)若函数 f ( x )= x ln( x +   )为偶函数,则 a = 　　          . 答案 　(1)D　(2)1 解析 　(1)① f ( x )=   +   的定义域为{-1,1}, 考点突破 又 f (- x )= ± f ( x )=0, 则 f ( x )=   +   既是奇函数又是偶函数. ② f ( x )= x 3 - x 的定义域为R, f (- x )=(- x ) 3 -(- x )=-( x 3 - x )=- f ( x ), 则 f ( x )= x 3 - x 是奇函数. ③由 x +   > x +| x | ≥ 0知 f ( x )=ln( x +   )的定义域为R, 又 f (- x )=ln(- x +   )=ln   =-ln( x +   )=- f ( x ),所以 f ( x )=ln( x +   )为奇函数. ④由   >0,得-1< x <1, 则 f ( x )=ln   的定义域为(-1,1), 又 f (- x )=ln   =ln   =-ln   =- f ( x ), 则 f ( x )为奇函数. ⑤要使 f ( x )有意义,则   ≥ 0, 解得-1< x ≤ 1,显然 f ( x )的定义域不关于原点对称, 所以 f ( x )既不是奇函数也不是偶函数. ⑥因为   所以-2 ≤ x ≤ 2且 x ≠ 0. 所以函数 f ( x )的定义域关于原点对称, 且 f ( x )=   =   , 所以 f (- x )=   =-   . 所以 f (- x )=- f ( x ),即函数 f ( x )是奇函数. ⑦当 x >0时,- x <0, f ( x )=- x 2 + x , ∴ f (- x )=(- x ) 2 - x = x 2 - x =-(- x 2 + x )=- f ( x ); 当 x <0时,- x >0, f ( x )= x 2 + x , ∴ f (- x )=-(- x ) 2 - x =- x 2 - x =-( x 2 + x )=- f ( x ). ∴对于 x ∈(- ∞ ,0) ∪ (0,+ ∞ ),均有 f (- x )=- f ( x ). ∴函数 f ( x )为奇函数.故选D. (2)由已知得 f (- x )= f ( x ),即- x ln(   - x )= x ln( x +   ),则ln( x +   )+ ln(   - x )=0, ∴ln[(   ) 2 - x 2 ]=0,得ln a =0,∴ a =1. 方法技巧 判断函数奇偶性的常用方法 1.定义法   2.图象法   3.性质法 在公共定义域内,(1)“奇+奇”是奇,“奇-奇”是奇,“奇·奇”是偶, “奇 ÷ 奇”是偶; (2)“偶+偶”是偶,“偶-偶”是偶,“偶·偶”是偶,“偶 ÷ 偶”是偶; (3)“奇·偶”是奇,“奇 ÷ 偶”是奇. 1-1 　设 f ( x )为定义在R上的奇函数,当 x ≥ 0时, f ( x )=2 x +2 x + b ( b 为常数),则 f (-1)=   (　　) A.-3　    B.-1　    C.1　    D.3 答案     A　∵ f ( x )为定义在R上的奇函数,∴ f (0)=0,∴ b =-1,∴ f (-1)=- f (1)= -(2+2-1)=-3. 1-2　函数 f ( x -1)是R上的奇函数, ∀ x 1 , x 2 ∈R,( x 1 - x 2 )·[ f ( x 1 )- f ( x 2 )]<0,则 f (1- x )< 0的解集是(　　) A.(- ∞ ,0)　    B.(0,+ ∞ ) C.(- ∞ ,2)　    D.(2,+ ∞ ) 答案     C　由于函数 f ( x -1)是R上的奇函数,故有 f (- x -1)=- f ( x -1),令 x =0,则 有 f (-1)=- f (-1),于是有 f (-1)=0. ∀ x 1 , x 2 ∈R,( x 1 - x 2 )[ f ( x 1 )- f ( x 2 )]<0,则函数 f ( x )在R上单调递减,不等式 f (1- x )<0 等价于 f (1- x )< f (-1),则有1- x >-1,解得 x <2,故选C. 1-3　已知函数 f ( x )= x 3 +sin x +1( x ∈R),若 f ( a )=2,则 f (- a )的值为   (　　) A.3　    B.0　    C.-1　    D.-2 答案     B　设 F ( x )= f ( x )-1= x 3 +sin x ,显然 F ( x )为奇函数,又 F ( a )= f ( a )-1=1,所 以 F (- a )= f (- a )-1=-1,从而 f (- a )=0.故选B. 考点二　函数周期性的判断与应用 典例2　 (1)(2016河南郑州模拟)已知函数 f ( x )=   如果对任 意的 n ∈N * ,定义 f n ( x )=   ( x )]},那么 f 2 016 (2)的值为   (　　) A.0　    B.1　    C.2　    D.3 (2)设定义在R上的函数 f ( x )满足 f ( x +2)= f ( x ),且当 x ∈[0,2)时, f ( x )=2 x - x 2 ,则 f (0)+ f (1)+ f (2)+ … + f (2 016)= 　　　     . 答案 　(1)C　(2)1 008 解析 　(1)∵ f 1 (2)= f (2)=1, f 2 (2)= f (1)=0, f 3 (2)= f (0)=2,∴ f n (2)的值具有周期 性,且周期为3,∴ f 2 016 (2)= f 3 × 672 (2)= f 3 (2)=2,故选C. (2)∵ f ( x +2)= f ( x ), ∴函数 f ( x )的周期 T =2, 又当 x ∈[0,2)时, f ( x )=2 x - x 2 ,所以 f (0)=0, f (1)=1, 所以 f (0)= f (2)= f (4)= … = f (2 016)=0, f (1)= f (3)= f (5)= … = f (2 015)=1. 故 f (0)+ f (1)+ f (2)+ … + f (2 016)=1 008. 规律总结 判断函数周期性的几个常用结论 若对于函数 f ( x )定义域内的任意一个 x 都有: (1) f ( x + a )=- f ( x )( a ≠ 0),则函数 f ( x )必为周期函数,2| a |是它的周期; (2) f ( x + a )=   ( a ≠ 0, f ( x ) ≠ 0),则函数 f ( x )必为周期函数,2| a |是它的周期; (3) f ( x + a )=-   ( a ≠ 0, f ( x ) ≠ 0),则函数 f ( x )必为周期函数,2| a |是它的周期. 2-1 　设 f ( x )是定义在R上的周期为3的函数,当 x ∈[-2,1)时, f ( x )=   则 f   =   (　　) A.0　    B.1　    C.   　    D.-1 答案     D　因为 f ( x )是周期为3的周期函数,所以 f   = f   = f   =4 ×   -2=-1,故选D. 2-2 　已知 f ( x )是定义在R上的偶函数,并且满足 f ( x +2)=   ,当2 ≤ x ≤ 3 时, f ( x )= x ,则 f (105.5)= 　　　     . 答案 　2.5 解析 　由 f ( x +2)=   得 f ( x +4)= f [( x +2)+2]=   =   = f ( x ),∴ f ( x )是 以4为周期的周期函数. ∴ f (105.5)= f (26 × 4+1.5)= f (1.5)= f (-2.5+4)= f (-2.5). ∵ f ( x )为偶函数,且当2 ≤ x ≤ 3时, f ( x )= x , ∴ f (105.5)= f (2.5)=2.5. 考点三　函数性质的综合问题 典例3　 (1)已知奇函数 f ( x )在(- ∞ ,0)上单调递减,且 f (2)=0,则不等式 ( x -1) f ( x -1)>0的解集为   (　　) A.(-3,-1)　    B.(-3,1) ∪ (2,+ ∞ ) C.(-3,0) ∪ (3,+ ∞ )　    D.(-1,1) ∪ (1,3) (2)已知 f ( x )是定义在R上的周期为2的奇函数,当 x ∈(0,1)时, f ( x )=3 x -1,则 f   =   (　　) A.   +1　    B.   -1　    C.-   -1　    D.-   +1 答案 　(1)D　(2)D 解析　 (1)原不等式可化为   ⇒   ⇒ 1< x <3; 或   ⇒   ⇒ -1< x <1. 综上,可知选D. (2)因为 f ( x +2)= f ( x )=- f (- x ), 所以 f   = f   = f   =- f   =- f   . 又当 x ∈(0,1)时, f ( x )=3 x -1, 所以 f   =   -1, 则 f   =1-   . 方法技巧 (1)利用函数性质求值的关键是利用函数的奇偶性、对称性以及函数的 周期性将自变量转化到指定区间内,然后代入函数解析式求值; (2)利用函数性质解不等式问题,主要利用函数的奇偶性与单调性等将 函数值的大小关系转化为自变量之间的大小关系求解. 3-1     (2016广东广州模拟)已知 f ( x )在R上是奇函数,且满足 f ( x +4)= f ( x ),当 x ∈(0,2)时, f ( x )=2 x 2 ,则 f (7)=   (　　) A.-2　    B.2　    C.-98　    D.98 答案     A　因为 f ( x +4)= f ( x ),所以函数 f ( x )的周期为4,所以 f (7)= f (7-8)= f (- 1),又因为 f ( x )为奇函数,且当 x ∈(0,2)时, f ( x )=2 x 2 ,所以 f (7)= f (-1)=- f (1)=-2, 故选A. 3-2　 已知函数 f ( x )是定义域为R的偶函数,且 f ( x +1)=   ,若 f ( x )在[-1,0] 上是减函数,那么 f ( x )在[2,3]上是   (　　) A.增函数　     B.减函数 C.先增后减的函数　     D.先减后增的函数 答案     A　由题意知 f ( x +2)=   = f ( x ),所以 f ( x )的周期为2,又函数 f ( x ) 是定义域为R的偶函数,且 f ( x )在[-1,0]上是减函数,则 f ( x )在[0,1]上是增函 数,所以 f ( x )在[2,3]上是增函数. 3-3　 已知定义在R上的奇函数 f ( x )满足 f ( x -4)=- f ( x ),且在区间[0,2]上是增 函数,则   (　　) A. f (-25)< f (11)< f (80)　    B. f (80)< f (11)< f (-25) C. f (11)< f (80)< f (-25)　    D. f (-25)< f (80)< f (11) 答案     D　∵ f ( x )= f ( x +4-4)=- f ( x +4)=- f ( x +8-4)= f ( x +8),∴ T =8. 又∵ f ( x )是定义在R上的奇函数, ∴ f (0)=0. ∵ f ( x )在(0,2)上是增函数,且 f ( x )>0, ∴ f ( x )在(-2,0)上也是增函数,且 f ( x )<0. ∴当 x ∈(2,4)时, f ( x )=- f ( x -4)>0,且 f ( x )为减函数. ∵ f (-25)= f (-1)<0, f (11)= f (3)>0, f (80)= f (0)=0, ∴ f (-25)< f (80)< f (11).故选D.