高考文科数学复习备课课件：第二节　参数方程 26页

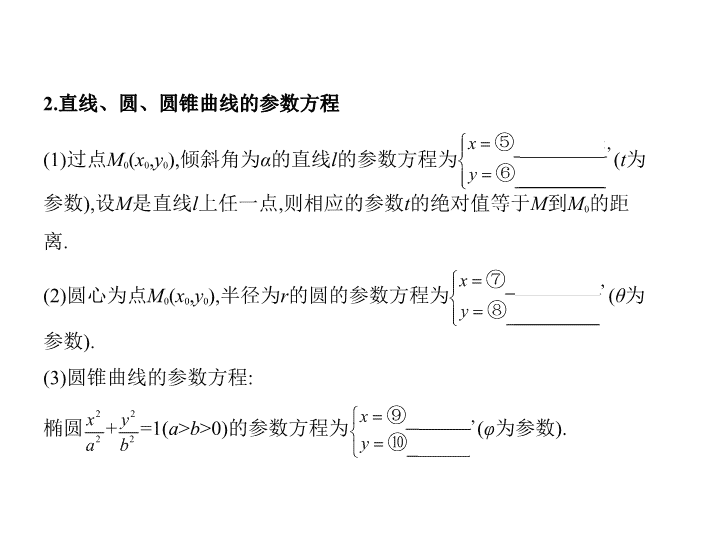
文数 课标 版 第二节　参数方程 教材研读 1 .参数方程的概念 一般地,在平面直角坐标系中,如果曲线 C 上① 　任意一点     P 的坐标 x , y 都是某个变数 t 的函数   并且对于 t 的每一个允许值,由   所 确定的点 P ( x , y )都在② 　曲线 C 上     ,那么   叫做这条曲线的参数 方程,变数 t 叫做参变数,简称③ 　参数     . 注意:相对于参数方程而言,直接给出点的坐标间关系的方程叫做 ④     普通方程     . 2.直线、圆、圆锥曲线的参数方程 (1)过点 M 0 ( x 0 , y 0 ),倾斜角为 α 的直线 l 的参数方程为   ( t 为 参数),设 M 是直线 l 上任一点,则相应的参数 t 的绝对值等于 M 到 M 0 的距 离. (2)圆心为点 M 0 ( x 0 , y 0 ),半径为 r 的圆的参数方程为   ( θ 为 参数). (3)圆锥曲线的参数方程: 椭圆   +   =1( a > b >0)的参数方程为   ( φ 为参数). 双曲线   -   =1( a >0, b >0)的参数方程为   ( φ 为参数). 抛物线 y 2 =2 px 的参数方程为   ( t 为参数).   1.已知直线 l 的参数方程为   ( t 为参数),则原点到 l 的距离为   (   　) A.1　    B.2　    C.3　    D.4 答案     C　由   ( t 为参数)消去 t 得4 x +3 y -15=0. ∴原点到直线 l 的距离 d =   =3,故选C. 2.曲线 C 的参数方程为   ( θ 为参数),则曲线 C 上的点 P 到原点 O 的距离的最大值为   (　　) A.1　    B.   　    C.   　    D.   答案     D　由   ( θ 为参数)消去参数 θ 得 y =-2 x 2 (-1 ≤ x ≤ 1).如图.   则当 P 点的坐标为( ± 1,-2)时, | PO | max =   =   ,故选D. 3.(2014北京,3,5分)曲线   ( θ 为参数)的对称中心(　　) A.在直线 y =2 x 上　    B.在直线 y =-2 x 上 C.在直线 y = x -1上　    D.在直线 y = x +1上 答案     B　曲线   ( θ 为参数)的普通方程为( x +1) 2 +( y -2) 2 =1,该 曲线为圆,圆心(-1,2)为曲线的对称中心,其在直线 y =-2 x 上,故选B. 4.已知两曲线的参数方程分别为   (0 ≤ θ <π)和   ( t ∈R), 则它们的交点坐标为 　　　     . 答案        1,     解析　 消去参数 θ 得普通方程为   + y 2 =1(0 ≤ y ≤ 1),表示椭圆的一部分. 消去参数 t 得普通方程为 y 2 =   x ,表示抛物线,联立两方程,可知两曲线有 一个交点,解得交点坐标为   1,     . 5.(2015湖北,16,5分)在直角坐标系 xOy 中,以 O 为极点, x 轴的正半轴为极 轴建立极坐标系.已知直线 l 的极坐标方程为 ρ (sin θ -3cos θ )=0,曲线 C 的 参数方程为   ( t 为参数), l 与 C 相交于 A , B 两点,则| AB |= 　　　     . 答案 　2   解析　 直线 l 的直角坐标方程为 y -3 x =0,曲线 C 的普通方程为 y 2 - x 2 =4. 由   得 x 2 =   ,即 x = ±   , 则| AB |=   | x A - x B |=   ×   =2   . 考点一　化参数方程为普通方程 典例1 　把下列参数方程化为普通方程,并说明它们各表示什么曲线. (1)   ( t 为参数);(2)   ( t 为参数). 解析 　(1)由 x =1+   t 得 t =2 x -2, ∴ y =2+   (2 x -2), ∴   x - y +2-   =0,此方程表示直线. (2)   由① 2 -② 2 得 x 2 - y 2 =4,此方程表示双曲线. 考点突破 方法技巧 化参数方程为普通方程的基本思路是消去参数,常用的消参方法有代入 法、加减法、恒等式(三角的或代数的)法.另外,消参时要注意参数的范 围. 1-1　 将下列参数方程化为普通方程. (1)   ( θ 为参数); (2)   ( t 为参数). 解析 　(1)由(sin θ +cos θ ) 2 =1+sin 2 θ =2-(1-sin 2 θ ), 得 y 2 =2- x .又 x =1-sin 2 θ ∈[0,2], 故所求的普通方程为 y 2 =2- x , x ∈[0,2]. (2)由参数方程得e t = x + y ,e - t = x - y , ∴( x + y )( x - y )=1, 即 x 2 - y 2 =1( x ≥ 1). 考点二　参数方程的应用 典例2     (2016豫南九校3月联考)在直角坐标系 xOy 中,设倾斜角为 α 的直 线 l :   ( t 为参数)与曲线 C :   ( θ 为参数)相交于不同的 两点 A , B . (1)若 α =   ,求线段 AB 的中点 M 的坐标; (2)若| PA |·| PB |=| OP | 2 ,其中 P (2,   ),求直线 l 的斜率. 解析 　(1)将曲线 C 的参数方程化为普通方程是   + y 2 =1. 当 α =   时,设点 M 对应的参数为 t 0 . 直线 l 的方程为   ( t 为参数), 代入曲线 C 的普通方程   + y 2 =1,得13 t 2 +56 t +48=0, 设直线 l 上的点 A , B 对应的参数分别为 t 1 , t 2 . 则 t 0 =   =-   ,所以点 M 的坐标为   . (2)将   代入曲线 C 的普通方程   + y 2 =1, 得(cos 2 α +4sin 2 α ) t 2 +(8   sin α +4cos α ) t +12=0, 因为| PA |·| PB |=| t 1 t 2 |=   ,| OP | 2 =7, 所以   =7,得tan 2 α =   . 由于 Δ =32cos α (2   sin α -cos α )>0, 故tan α =   .所以直线 l 的斜率为   . 方法技巧 在求解与参数方程有关的问题时,一般是将参数方程转化为我们所熟悉 的形式,即转化为普通方程,从而利用普通方程求解. 2-1 　已知曲线 C 的参数方程为   ( θ 为参数),在同一平面直角坐 标系中,将曲线 C 上的点按坐标变换   得到曲线 C '. (1)求曲线 C '的普通方程; (2)已知点 A 在曲线 C '上,点 D (1,3),当点 A 在曲线 C '上运动时,求 AD 的中点 P 的轨迹方程. 解析 　(1)将   代入   得曲线 C '的参数方程,为   ∴曲线 C '的普通方程为   + y 2 =1. (2)设点 P ( x , y ), A ( x 0 , y 0 ), ∵ D (1,3),且 AD 的中点为 P , ∴   ∴   又点 A 在曲线 C '上, ∴代入 C '的普通方程   + y 2 =1, 得(2 x -1) 2 +4(2 y -3) 2 =4, ∴动点 P 的轨迹方程为(2 x -1) 2 +4(2 y -3) 2 =4. 2-2     (2014课标Ⅰ,23,10分)已知曲线 C :   +   =1,直线 l :   ( t 为参 数). (1)写出曲线 C 的参数方程,直线 l 的普通方程; (2)过曲线 C 上任意一点 P 作与 l 夹角为30 ° 的直线,交 l 于点 A ,求| PA |的最大 值与最小值. 解析 　(1)曲线 C 的参数方程为   ( θ 为参数). 直线 l 的普通方程为2 x + y -6=0. (2)曲线 C 上任意一点 P (2cos θ ,3sin θ )到 l 的距离为 d =   |4cos θ +3sin θ -6|. 则| PA |=   =   |5sin( θ + α )-6|, 其中 α 为锐角,且tan α =   . 当sin( θ + α )=-1时,| PA |取得最大值,最大值为   . 当sin( θ + α )=1时,| PA |取得最小值,最小值为   . 考点三　极坐标方程与参数方程的综合问题 典例3     (2016课标全国Ⅱ,23,10分)在直角坐标系 xOy 中,圆 C 的方程为( x +6) 2 + y 2 =25. (1)以坐标原点为极点, x 轴正半轴为极轴建立极坐标系,求 C 的极坐标方 程; (2)直线 l 的参数方程是   ( t 为参数), l 与 C 交于 A , B 两点,| AB |=   , 求 l 的斜率. 解析 　(1)由 x = ρ cos θ , y = ρ sin θ 可得圆 C 的极坐标方程为 ρ 2 +12 ρ cos θ +11= 0. (2)在(1)中建立的极坐标系中,直线 l 的极坐标方程为 θ = α ( ρ ∈R). 设 A , B 所对应的极径分别为 ρ 1 , ρ 2 ,将 l 的极坐标方程代入 C 的极坐标方程 得 ρ 2 +12 ρ cos α +11=0. 于是 ρ 1 + ρ 2 =-12cos α , ρ 1 ρ 2 =11. | AB |=| ρ 1 - ρ 2 |=   =   . 由| AB |=   得cos 2 α =   ,tan α = ±   . 所以 l 的斜率为   或-   . 方法技巧 处理极坐标、参数方程综合问题的方法 (1) 涉及参数方程和极坐标方程的综合题 , 求解的一般方法是分别化为 普通方程和直角坐标方程后求解 . 当然 , 还要结合题目本身的特点 , 确定 选择何种方程. (2)充分利用参数方程中参数的几何意义,或者利用 ρ 和 θ 的几何意义直 接求解,能达到化繁为简的解题目的. 3-1     (2015课标Ⅱ,23,10分)在直角坐标系 xOy 中,曲线 C 1 :   ( t 为 参数, t ≠ 0),其中0 ≤ α <π.在以 O 为极点, x 轴正半轴为极轴的极坐标系中, 曲线 C 2 : ρ =2sin θ , C 3 : ρ =2   cos θ . (1)求 C 2 与 C 3 交点的直角坐标; (2)若 C 1 与 C 2 相交于点 A , C 1 与 C 3 相交于点 B ,求| AB |的最大值. 解析 　(1)曲线 C 2 的直角坐标方程为 x 2 + y 2 -2 y =0,曲线 C 3 的直角坐标方程 为 x 2 + y 2 -2   x =0. 联立   解得   或   所以 C 2 与 C 3 交点的直角坐标为(0,0)和   . (2)曲线 C 1 的极坐标方程为 θ = α ( ρ ∈R, ρ ≠ 0), 其中0 ≤ α <π. 因此 A 的极坐标为(2sin α , α ), B 的极坐标为(2   cos α , α ). 所以| AB |=|2sin α -2   cos α |=4   . 当 α =   时,| AB |取得最大值,最大值为4. 3-2     (2016湖南长沙模拟)在直角坐标系 xOy 中,曲线 C 1 的参数方程为   ( α 为参数),以原点 O 为极点, x 轴正半轴为极轴,建立极坐标 系,直线 l 的极坐标方程为 ρ (cos θ + k sin θ )=-2( k 为实数). (1)判断直线 l 与曲线 C 1 的位置关系,并说明理由; (2)若曲线 C 1 和直线 l 相交于 A , B 两点,且| AB |=   ,求直线 l 的斜率. 解析 　(1)直线 l 与曲线 C 1 相切或相交.理由如下: 由曲线 C 1 的参数方程   可得其普通方程为( x +1) 2 + y 2 =1. 由 ρ (cos θ + k sin θ )=-2可得直线 l 的直角坐标方程为 x + ky +2=0. 因为圆心(-1,0)到直线 l 的距离 d =   ≤ 1,所以直线与圆相交或相切, 当 k =0时,直线 l 与曲线 C 1 相切; 当 k ≠ 0时,直线 l 与曲线 C 1 相交. (2)由于曲线 C 1 和直线 l 相交于 A , B 两点,且| AB |=   ,故圆心到直线 l 的距离 d =   =   =   ,解得 k = ± 1,所以直线 l 的斜率为 ± 1.