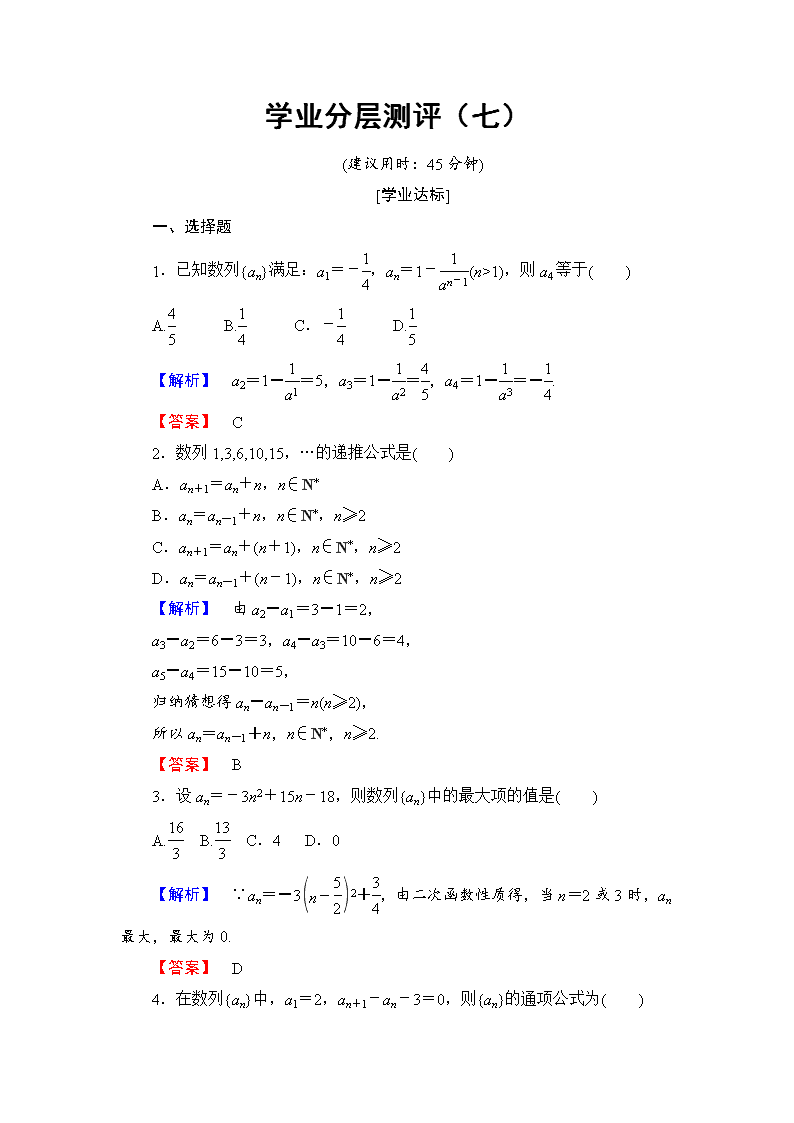高中数学人教a必修5学业分层测评7数列的通项与递推公式word版含解析 6页

学业分层测评（七） (建议用时：45 分钟) [学业达标] 一、选择题 1．已知数列{an}满足：a1＝－1 4 ，an＝1－ 1 an－1 (n>1)，则 a4 等于( ) A.4 5 B.1 4 C．－1 4 D.1 5 【解析】 a2＝1－ 1 a1 ＝5，a3＝1－ 1 a2 ＝4 5 ，a4＝1－ 1 a3 ＝－1 4. 【答案】 C 2．数列 1,3,6,10,15，…的递推公式是( ) A．an＋1＝an＋n，n∈N* B．an＝an－1＋n，n∈N*，n≥2 C．an＋1＝an＋(n＋1)，n∈N*，n≥2 D．an＝an－1＋(n－1)，n∈N*，n≥2 【解析】 由 a2－a1＝3－1＝2， a3－a2＝6－3＝3，a4－a3＝10－6＝4， a5－a4＝15－10＝5， 归纳猜想得 an－an－1＝n(n≥2)， 所以 an＝an－1＋n，n∈N*，n≥2. 【答案】 B 3．设 an＝－3n2＋15n－18，则数列{an}中的最大项的值是( ) A.16 3 B.13 3 C．4 D．0 【解析】 ∵an＝－3 n－5 2 2＋3 4 ，由二次函数性质得，当 n＝2 或 3 时，an 最大，最大为 0. 【答案】 D 4．在数列{an}中，a1＝2，an＋1－an－3＝0，则{an}的通项公式为( ) A．an＝3n＋2 B．an＝3n－2 C．an＝3n－1 D．an＝3n＋1 【解析】 因为 a1＝2，an＋1－an－3＝0， 所以 an－an－1＝3， an－1－an－2＝3， an－2－an－3＝3， … a2－a1＝3， 以上各式相加， 则有 an－a1＝(n－1)×3， 所以 an＝2＋3(n－1)＝3n－1. 【答案】 C 5．已知在数列{an}中，a1＝3，a2＝6，且 an＋2＝an＋1－an，则 a2 016＝( ) A．3 B．－3 C．6 D．－6 【解析】 由题意知：a3＝a2－a1＝3，a4＝a3－a2＝－3， a5＝a4－a3＝－6，a6＝a5－a4＝－3， a7＝a6－a5＝3，a8＝a7－a6＝6， a9＝a8－a7＝3，a10＝a9－a8＝－3， … 故知{an}是周期为 6 的数列， ∴a2 016＝a6＝－3. 【答案】 B 二、填空题 6 ． 数 列 {an} 中 ， 若 an ＋ 1 － an － n ＝ 0 ， 则 a2 016 － a2 015 ＝ . 【解析】 由已知 a2 016－a2 015－2 015＝0， ∴a2 016－a2 015＝2 015. 【答案】 2 015 7．数列{an}满足 an＝4an－1＋3，且 a1＝0，则此数列的第 5 项是 ． 【解析】 因为 an＝4an－1＋3，所以 a2＝4×0＋3＝3， a3＝4×3＋3＝15，a4＝4×15＋3＝63，a5＝4×63＋3＝255. 【答案】 255 8．数列{an}满足：a1＝6，a1＋a2＋a3＋…＋an＝3 2an－3，那么这个数列的通 项公式为 ． 【解析】 由 a1＋a2＋a3＋…＋an＝3 2an－3， 得 a1＋a2＋a3＋…＋an－1＝3 2an－1－3(n≥2)， 两式作差得 3an－1＝an(n≥2)， ∴an＝a1·a2 a1 ·a3 a2 ·…· an an－1 ＝6·3n－1＝2·3n(n≥2)． ∵a1＝6 也适合上式， ∴an＝2·3n(n∈N*)(n∈N*)． 【答案】 an＝2·3n(n∈N*) 三、解答题 9．已知数列{an}中，a1＝1，an＋1＝ 3an an＋3(n∈N*)，求通项 an. 【解】 将 an＋1＝ 3an an＋3 两边同时取倒数得： 1 an＋1 ＝an＋3 3an ， 则 1 an＋1 ＝1 an ＋1 3 ， 即 1 an＋1 －1 an ＝1 3 ， ∴ 1 a2 － 1 a1 ＝1 3 ， 1 a3 － 1 a2 ＝1 3 ，…， 1 an － 1 an－1 ＝1 3 ， 把以上这(n－1)个式子累加， 得 1 an － 1 a1 ＝n－1 3 . ∵a1＝1，∴an＝ 3 n＋2(n∈N*)． 10．已知数列{an}的通项公式 an＝(n＋2)· 6 7 n，试求数列{an}的最大项. 【导 学号：05920065】 【解】 假设第 n 项 an 为最大项，则 an≥an－1， an≥an＋1. 即 n＋2· 6 7 n≥n＋1· 6 7 n－1， n＋2· 6 7 n≥n＋3· 6 7 n＋1. 解得 n≤5， n≥4， 即 4≤n≤5， 所以 n＝4 或 5，故数列{an}中 a4 与 a5 均为最大项，且 a4＝a5＝65 74. [能力提升] 1．已知数列{an}对任意的 p，q∈N*满足 ap＋q＝ap＋aq，且 a2＝－6，那么 a10 等于( ) A．－165 B．－33 C．－30 D．－21 【解析】 由已知得 a2＝a1＋a1＝2a1＝－6，∴a1＝－3. ∴a10＝2a5＝2(a2＋a3) ＝2a2＋2(a1＋a2) ＝4a2＋2a1＝4×(－6)＋2×(－3)＝－30. 【答案】 C 2．(2015·吉林高二期末)已知函数 f(x)＝ x＋1 2 ，x≤1 2 ， 2x－1，1 2