高中数学第二章函数2_3函数的单调性问题导学案北师大版必修11 7页

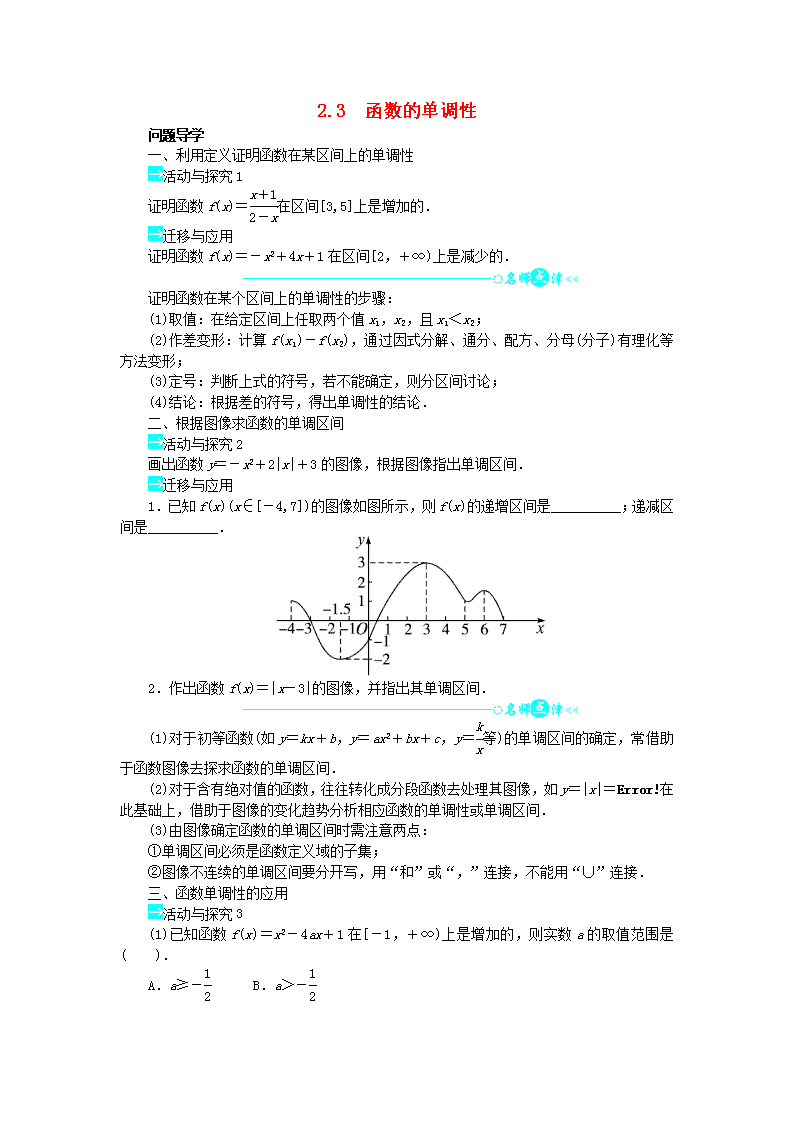
2.3 函数的单调性 问题导学 一、利用定义证明函数在某区间上的单调性 活动与探究 1 证明函数 f(x)＝x＋1 2－x 在区间[3,5]上是增加的． 迁移与应用 证明函数 f(x)＝－x2＋4x＋1 在区间[2，＋∞)上是减少的． 证明函数在某个区间上的单调性的步骤： (1)取值：在给定区间上任取两个值 x1，x2，且 x1＜x2； (2)作差变形：计算 f(x1)－f(x2)，通过因式分解、通分、配方、分母(分子)有理化等 方法变形； (3)定号：判断上式的符号，若不能确定，则分区间讨论； (4)结论：根据差的符号，得出单调性的结论． 二、根据图像求函数的单调区间 活动与探究 2 画出函数 y＝－x2＋2|x|＋3 的图像，根据图像指出单调区间． 迁移与应用 1．已知 f(x)(x∈[－4,7])的图像如图所示，则 f(x)的递增区间是__________；递减区 间是__________． 2．作出函数 f(x)＝|x－3|的图像，并指出其单调区间． (1)对于初等函数(如 y＝kx＋b，y＝ax2＋bx＋c，y＝k x 等)的单调区间的确定，常借助于 函数图像去探求函数的单调区间． (2)对于含有绝对值的函数，往往转化成分段函数去处理其图像，如 y＝|x|＝ x，x≥0， －x，x<0， 在此基础上，借助于图像的变化趋势分析相应函数的单调性或单调区间． (3)由图像确定函数的单调区间时需注意两点： ①单调区间必须是函数定义域的子集； ②图像不连续的单调区间要分开写，用“和”或“，”连接，不能用“∪”连接． 三、函数单调性的应用 活动与探究 3 (1)已知函数 f(x)＝x2－4ax＋1 在[－1，＋∞)上是增加的，则实数 a 的取值范围是 ( )． A．a≥－1 2 B．a＞－1 2 C．a≤－1 2 D．a＝－1 2 (2)已知 y＝f(x)在定义域(－1,1)上是减函数，且 f(1－a)＜f(2a－1)，求 a 的取值范 围． 迁移与应用 (1)设 f(x)是(－∞，＋∞)上的减函数，则( )． A．f(1)＞f(2) B．f(－a)＜f(a) C．f(0)＜f(a) D．f(1)＜f(2) (2)若函数 f(x)＝(4a－3)x＋2 在 R 上是减函数，则实数 a 的取值范围是__________． (3)已知 f(x)是定义在 R 上的增函数，且 f(x－2)＜f(1－x)，求 x 的取值范围． (1)已知二次函数在某一区间上的单调性求参数的取值范围时，要结合函数的图像，分 析抛物线的开口方向，根据对称轴与给定区间的位置关系，建立关于参数的不等式，从而求 得参数的取值范围． (2)根据函数的单调性比较函数值的大小时，首先应明确函数的单调性及单调区间，然 后分析欲比较大小的函数值相对应的自变量的所属区间及其大小关系，最后利用单调性确定 函数值的大小． (3)由函数值的大小关系确定变量的取值范围时，关键是根据函数的单调性，将函数值 的大小关系转换为相应自变量的大小关系，从而建立不等式求出参数的取值范围，但务必注 意函数定义域对参数取值的限制，不可忽视定义域． 四、利用函数的单调性求最值 活动与探究 4 (1)求函数 f(x)＝－x2＋2x 在区间[0，＋∞)上的最大值； (2)求函数 f(x)＝ 2 －x－1 在区间[2,6]上的最大值和最小值． 迁移与应用 (1)函数 f(x)＝4－5x 在区间[－1,2]上的最小值等于__________． (2)若函数 f(x)＝ 1 x－1 ，x∈[3,4]，求 f(x)的最值． 1．熟记运用函数单调性求最值的步骤 (1)判断：先判断函数的单调性． (2)求值：利用单调性代入自变量的值求得最值． 2．明确利用单调性求最大值、最小值易出错的几点 (1)写出最值时要写最高(低)点的纵坐标，而不是横坐标． (2)求最值忘记求定义域． (3)求最值，尤其是闭区间上的最值，不判断单调性而直接将两端点值代入． 当堂检测 1．函数 f(x)＝－x2 的递增区间为( )． A．(－∞，0] B．[0，＋∞) C．(－∞，＋∞) D．(－1，＋∞) 2．若 f(x)＝(2a－1)x＋b 是 R 上的减函数，则有( )． A．a≥1 2 B．a≤1 2 C．a＞－1 2 D．a＜1 2 3．函数 f(x)＝x2－4 在区间[－2，－1]上的最大值是( )． A．0 B．－3 C．3 D．1 4．若 f(x)是 R 上的增函数，且 f(x－1)＞f(2)，则 x 的取值范围是__________． 5．证明函数 f(x)＝x＋4 x 在(2，＋∞)上是增加的． 提示：用最精炼的语言把你当堂掌握的核心知识的精华 部分和基本技能的要领部分写下来并进行识记。 答案： 课前预习导学 【预习导引】 1．定义域内 任意两数 f(x1)＜f(x2) 增加的 递增 定义域内 任意两数 f(x1)＞f(x2) 减少的 递减 预习交流 1 提示：不可以．如图，虽然 f(－1)＜f(2)，但 f(x)在[－1,2]上既不是增 加的，也不是减少的． 2．增加 减少 单调区间 单调性 增加的 减少的 单调函数 预习交流 2 (1)提示：不能用“∪”来连接，而应该用“和”来连接．如函数 y＝1 x ， 其定义域为(－∞，0)∪(0，＋∞)，不能说函数在(－∞，0)∪(0，＋∞)上递减，而只能说 函数在(－∞，0)和(0，＋∞)上递减． (2)提示：不一定，例如函数 y＝x2 在其定义域 R 上不具有单调性． (3)提示：如果 f(x)在[a，b]上是增加的，那么由 f(x1)＞f(x2)可得 x1＞x2；如果 f(x) 在[a，b]上是减少的，那么由 f(x1)＞f(x2)可得 x1＜x2. 3．上升 减少 4．(1)①f(x)≤M ②f(x0)＝M (2)①f(x)≥M ②f(x0)＝M 预习交流 3 提示： 在[a，b]上的单调 性 在[a，b]上的最大值 在[a，b]上的最小值 在[a，b]上增加 f(b) f(a) 在[a，b]上减少 f(a) f(b) 在[a，c]上增加， 在[c，b]上减少 f(c) f(a)与 f(b) 中的较小者 在[a，c]上减少， 在[c，b]上增加 f(a)与 f(b) 中的较大者 f(c) 课堂合作探究 【问题导学】 活动与探究 1 思路分析：利用函数增减性的定义来证明，其关键是对 f(x1)－f(x2)进 行变形，尽量化成几个最简单因式的乘积的形式． 证明：设 x1，x2 是区间[3,5]上的任意两个实数，且 x1＜x2， 则 f(x1)－f(x2)＝x1＋1 2－x1 －x2＋1 2－x2 ＝ 3(x1－x2) (2－x1)(2－x2) . 因为 3≤x1＜x2≤5， 所以 2－x1＜0,2－x2＜0，x1－x2＜0. 所以 f(x1)－f(x2)＜0， 即 f(x1)＜f(x2)． 所以 f(x)在[3,5]上是增加的． 迁移与应用 证明：设 x1，x2 是区间[2，＋∞)上的任意两个实数，且 x1＜x2， 则 f(x1)－f(x2)＝(－x2 1＋4x1＋1)－(－x2 2＋4x2＋1) ＝(x2 2－x2 1)＋4(x1－x2)＝(x1－x2)(4－x1－x2)． 因为 2≤x1＜x2， 所以 x1－x2＜0,4－x1－x2＜0， 所以 f(x1)－f(x2)＞0，即 f(x1)＞f(x2)． 所以 f(x)在[2，＋∞)上是减少的． 活动与探究 2 思路分析：先去掉绝对值，将函数化为分段函数，再画出每一段上的图 像，最后指出单调区间． 解：y＝－x2＋2|x|＋3＝ －x2＋2x＋3，x≥0， －x2－2x＋3，x<0， 即 f(x)＝ －(x－1)2＋4，x≥0， －(x＋1)2＋4，x<0. 其图像如图所示． 由图像可知，f(x)的递增区间为(－∞，－1]和[0,1]，递减区间为[－1,0]和[1，＋∞)． 迁移与应用 1.[－1.5,3]和[5,6]，[－4，－1.5]和[3,5]和[6,7] 2．解：f(x)= 3, 3, 3 , 3. x x x x      作出函数的图像如图，由图知函数的递增区间是[3，＋∞)， 递减区间是(－∞，3]． 活动与探究 3 思路分析：(1)函数 f(x)为二次函数，图像是抛物线，求出其对称轴， 结合图像及已知条件分析对称轴与所给区间的位置关系，从而确定 a 的取值范围； (2)不等式 f(1－a)＜f(2a－1)为抽象不等式，不能直接求解．考虑到函数的单调性， 可将函数值的不等关系转化为自变量取值的不等关系，即转化为具体不等式来求解． (1)C 解析：f(x)＝x2－4ax＋1 的图像开口向上，对称轴为 x＝2a.∵f(x)在[－1，＋ ∞)上是增加的， ∴2a≤－1，即 a≤－1 2 . ∴a 的取值范围为 a≤－1 2 . (2)解：由题意可知 －1<1－a<1， －1<2a－1<1， 解得 0＜a＜1.① ∵f(x)在(－1,1)上是减函数，且 f(1－a)＜f(2a－1)， ∴1－a＞2a－1，即 a＜2 3 .② 由①②可知，0＜a＜2 3 . 即所求 a 的取值范围是 0＜a＜2 3 . 迁移与应用 (1)A 解析：由于－a 与 a、0 与 a 的大小关系不确定，所以 f(－a)与 f(a)、 f(0)与 f(a)的大小关系也不确定，故 B、C 均错；又因为 f(x)在 R 上递减，故 f(1)＞f(2)， 故 D 错，A 正确． (2)a＜3 4 解析：要使 f(x)＝(4a－3)x＋2 在 R 上是减函数，应满足 4a－3＜0，解得 a ＜3 4 . (3)解：∵f(x)是定义在 R 上的增函数， 且 f(x－2)＜f(1－x)， ∴x－2＜1－x.∴x＜3 2 ， 即 x 的取值范围是 －∞，3 2 . 活动与探究 4 思路分析：(1)结合函数 f(x)的图像分析 f(x)的单调性，从而确定其最 大值； (2)利用函数增加、减少的定义判断 f(x)在[2,6]上的单调性，再求最值． 解：(1)画出函数 f(x)＝－x2＋2x 的图像(如图)，由图像可知：f(x)在[0,1]上是增加 的，在[1，＋∞)上是减少的，所以 f(x)在[0，＋∞)上的最大值是 f(1)＝1. (2)任取 x1，x2∈[2,6]，且 x1＜x2，则 f(x2)－f(x1)＝ 2 －x2－1 － 2 －x1－1 ＝ 2(x2－x1) (x2＋1)(x1＋1) . 因为 2≤x1＜x2≤6， 所以 x2－x1＞0，(x2＋1)(x1＋1)＞0， 于是 2(x2－x1) (x2＋1)(x1＋1) ＞0，即 f(x1)＜f(x2)， 所以函数 f(x)＝ 2 －x－1 在区间[2,6]上是增加的，所以函数 f(x)＝ 2 －x－1 在区间[2,6] 的左、右端点处分别取得最小值、最大值，即最大值为 f(6)＝ 2 －6－1 ＝－2 7 ，最小值为 f(2) ＝ 2 －2－1 ＝－2 3 . 迁移与应用 (1)－6 解析：显然 f(x)＝4－5x 在区间[－1,2]上是减少的，所以最小 值等于 f(2)＝－6. (2)解：在[3,4]上任取两个值 x1，x2 且 x1＜x2， 则 x2－x1＞0，f(x2)－f(x1)＝ 1 x2－1 － 1 x1－1 ＝x1－1－(x2－1) (x2－1)(x1－1) ＝ x1－x2 (x2－1)(x1－1) . ∵x1，x2∈[3,4]，∴(x2－1)(x1－1)＞0， x1－x2＜0.∴f(x2)＜f(x1)． ∴f(x)＝ 1 x－1 在[3,4]上是减少的． ∴f(x)的最大值为 f(3)＝1 2 ，f(x)的最小值为 f(4)＝1 3 . 【当堂检测】 1．A 2．D 解析：∵f(x)是 R 上的减函数， ∴2a－1＜0.∴a＜1 2 . 3．A 解析：由图像易知 f(x)＝x2－4 在区间[－2，－1]上是递减的，故其最大值为 f(－ 2)＝0. 4．(3，＋∞) 解析：∵f(x)是 R 上的增函数，且 f(x－1)＞f(2)，∴x－1＞2，∴x＞ 3. 5．证明：任取 x1，x2∈(2，＋∞)，且 x1＜x2， 则 f(x2)－f(x1)＝x2＋4 x2 －x1－4 x1 ＝(x2－x1)＋4(x1－x2) x1x2 ＝(x2－x1)x1x2－4 x1x2 . ∵2＜x1＜x2，∴x2－x1＞0，x1x2＞4，x1x2－4＞0. ∴f(x2)＞f(x1)． ∴函数 f(x)＝x＋4 x 在(2，＋∞)上是增加的．