2021届高考数学一轮总复习课时作业26正弦定理和余弦定理的应用含解析苏教版 6页

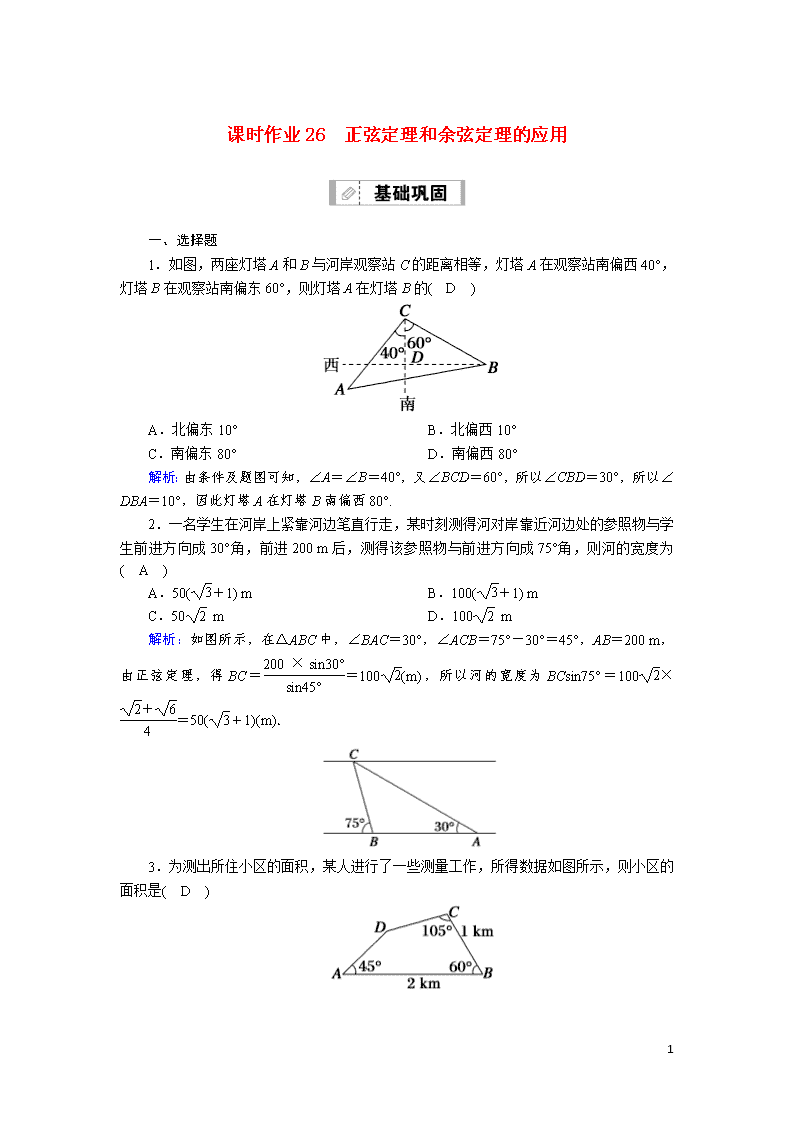
课时作业26　正弦定理和余弦定理的应用 一、选择题 ‎1．如图，两座灯塔A和B与河岸观察站C的距离相等，灯塔A在观察站南偏西40°，灯塔B在观察站南偏东60°，则灯塔A在灯塔B的(　D　)‎ A．北偏东10° B．北偏西10°‎ C．南偏东80° D．南偏西80°‎ 解析：由条件及题图可知，∠A＝∠B＝40°，又∠BCD＝60°，所以∠CBD＝30°，所以∠DBA＝10°，因此灯塔A在灯塔B南偏西80°.‎ ‎2．一名学生在河岸上紧靠河边笔直行走，某时刻测得河对岸靠近河边处的参照物与学生前进方向成30°角，前进200 m后，测得该参照物与前进方向成75°角，则河的宽度为(　A　)‎ A．50(＋1) m B．100(＋1) m C．50 m D．100 m 解析：如图所示，在△ABC中，∠BAC＝30°，∠ACB＝75°－30°＝45°，AB＝200 m，由正弦定理，得BC＝＝100(m)，所以河的宽度为BCsin75°＝100×＝50(＋1)(m)．‎ ‎3．为测出所住小区的面积，某人进行了一些测量工作，所得数据如图所示，则小区的面积是(　D　)‎ 6‎ A． km2‎ B． km2‎ C． km2‎ D． km2‎ 解析：连接AC，根据余弦定理可得AC＝ km，故△ABC为直角三角形．且∠ACB＝90°，∠BAC＝30°，故△ADC为等腰三角形，设AD＝DC＝x km，根据余弦定理得x2＋x2＋x2＝3，即x2＝＝3×(2－)，所以所求的面积为×1×＋×3×(2－)×＝＝(km2)．‎ ‎4．(2020·四平质检)在△ABC中，已知a，b，c分别为角A，B，C的对边且∠A＝60°，若S△ABC＝且2sinB＝3sinC，则△ABC的周长等于(　A　)‎ A．5＋ B．12‎ C．10＋ D．5＋2 解析：在△ABC中，∠A＝60°.∵2sinB＝3sinC，∴由正弦定理可得2b＝3c，再由S△ABC＝＝bc·sinA，可得bc＝6，∴b＝3，c＝2.由余弦定理可得a2＝b2＋c2－2bc·cosA＝7，∴a＝，故△ABC的周长为a＋b＋c＝5＋，故选A．‎ ‎5．(2020·安徽联考)如图，在△ABC中，BD·sinB＝CD·sinC，BD＝2DC＝2，AD＝2，则△ABC的面积为(　B　)‎ A． B． C．3 D．3 解析：过点D分别作AB和AC的垂线，垂足分别为E，F.由BD·sinB＝CD·sinC得DE＝DF，则AD为∠BAC的平分线，∴＝＝2，又cos∠ADB＋cos∠ADC＝0，即＝－，解得AC＝2.则AB＝4.‎ 在△ABC中，cos∠BAC＝＝，‎ ‎∴sin∠BAC＝，∴S△ABC＝AB·AC·sin∠BAC＝.‎ ‎6．(2020·安徽名校联考)在△ABC中，角A，B，C所对的边分别为a，b，c，若bc＝1，‎ 6‎ b＋2ccosA＝0，则当角B取得最大值时，△ABC的周长为(　A　)‎ A．2＋　　　B．2＋　　　C．3　　　D．3＋ 解析：由题及正弦定理可得，sinB＋2sinCcosA＝0，即sin(A＋C)＋2sinCcosA＝0，得sinAcosC＝－3sinCcosA，即tanA＝－3tanC．又cosA＝－<0，所以A为钝角，于是tanC>0.从而tanB＝－tan(A＋C)＝－＝＝，由基本不等式，得＋3tanC≥2 ＝2，当且仅当tanC＝时等号成立，此时角B取得最大值，且tanB＝tanC＝，tanA＝－，即b＝c，A＝120°，又bc＝1，所以b＝c＝1，a＝，故△ABC的周长为2＋.故选A．‎ 二、填空题 ‎7．如图所示，测量河对岸的塔高AB时可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD＝15°，∠BDC＝30°，CD＝30，并在点C测得塔顶A的仰角为60°，则塔高AB等于15.‎ 解析：在△BCD中，∠CBD＝180°－15°－30°＝135°.‎ 由正弦定理得＝，‎ 所以BC＝15.‎ 在Rt△ABC中，AB＝BCtan∠ACB＝15×＝15.‎ ‎8．如图所示，在△ABC中，C＝，BC＝4，点D在边AC上，AD＝DB，DE⊥AB，E为垂足，若DE＝2，则cosA＝.‎ 解析：∵AD＝DB，∴∠A＝∠ABD，∠BDC＝2∠A．设AD＝BD＝x，∴在△BCD中，＝，可得＝.①‎ 6‎ 在△AED中，＝，可得＝.②‎ ‎∴联立①②可得＝，解得cosA＝.‎ ‎9．在△ABC中，已知BC＝2，·＝2，则△ABC面积的最大值是.‎ 解析：由＝－，得2＝(－)2，设||＝c，||＝b，则b2＋c2＝8，又因为·＝bc·cosA＝2，所以cosA＝，所以sin2A＝1－，设△ABC的面积为S，则S2＝(bc)2sin2A＝(b2c2－4)，因为bc≤＝4，所以S2≤3(当且仅当b＝c＝2时取等号)，所以S≤.所以△ABC面积的最大值是.‎ ‎10．(2020·洛阳统考)在△ABC中，角A，B，C所对的边分别为a，b，c，若a，b，c成等比数列，且tanB＝，则＋的值是.‎ 解析：∵a，b，c成等比数列，‎ ‎∴b2＝ac，由正弦定理得sin2B＝sinAsinC，‎ ‎∴＋＝＋ ‎＝＝＝＝，∵tanB＝，∴sinB＝，∴＋＝.‎ 三、解答题 ‎11．在△ABC中，AB＝6，AC＝4.‎ ‎(1)若sinB＝，求△ABC的面积；‎ ‎(2)若＝2，AD＝3，求BC的长．‎ 解：(1)由正弦定理得＝，所以sinC＝1，‎ 因为0