2015年数学理高考课件4-1 平面向量的概念及线性运算 36页

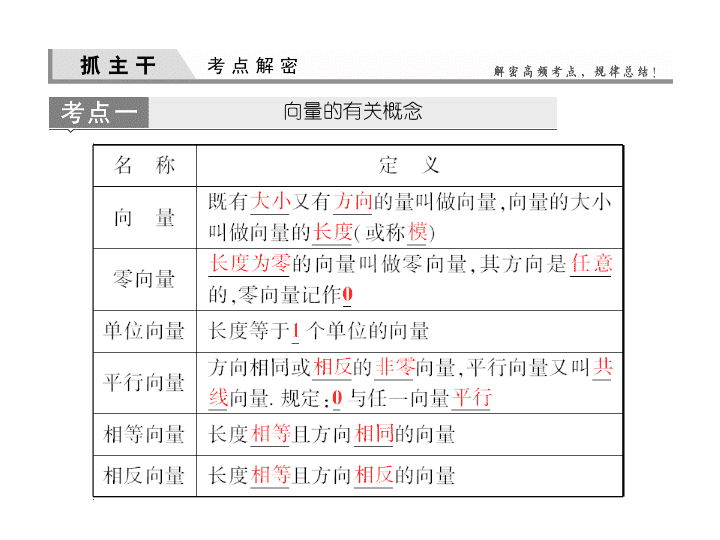
第四章　平面向量、复数 [ 最新考纲展示 ] 　 1 ． 了解向量的实际背景．　 2. 理解平面向量的概念，理解两个向量相等的含义．　 3. 理解向量的几何表示．　 4. 掌握向量加法、减法的运算，并理解其几何意义．　 5. 掌握向量数乘的运算及其几何意义，理解两个向量共线的含义．　 6. 了解向量线性运算的性质及其几何意义． 第一节　平面向量的概念及线性运算 向量的有关概念 ____________________[ 通关方略 ]____________________ 1 ． 向量与有向线段 向量常用有向线段表示，它们是两个不同概念，有向线段由起点、终点方向唯一确定，而向量是由大小和方向来确定的． 2 ．零向量和单位向量是两个特殊的向量．它们的模确定，但方向不确定，在解题时注意它们的特殊性．如若 a ∥ b 、 b ∥ c 则 a ∥ c 是假命题，因为当 b 为零向量时， b 与 c 为任意向量，两者不一定平行． 3 ．共线向量也叫平行向量，两向量所在的直线可以共线也可以平行． 4 ．相等向量一定是平行向量． 1 ．设 a 0 为单位向量， ① 若 a 为平面内的某个向量，则 a ＝ | a | a 0 ； ② 若 a 与 a 0 平行，则 a ＝ | a | a 0 ； ③ 若 a 与 a 0 平行且 | a | ＝ 1 ，则 a ＝ a 0 . 上述命题中，假命题的个数是 ( 　　 ) A ． 0 　　　　 B ． 1 　　　　 C ． 2 　　　　 D ． 3 解析： 向量是既有大小又有方向的量， a 与 | a | a 0 的模相等，但方向不一定相同，故 ① 是假命题；若 a 与 a 0 平行，则 a 与 a 0 的方向有两种情况：一是同向，二是反向，反向时 a ＝－ | a | a 0 ，故 ②③ 也是假命题．综上所述，假命题的个数是 3. 答案： D 2 ．下列说法中正确的是 ( 　　 ) A ．只有方向相同或相反的向量是平行向量 B ．零向量的长度为零 C ．长度相等的两个向量是相等向量 D ．共线向量是在一条直线上的向量 解析： 由于零向量与任意向量平行，故选项 A 错误；长度相等且方向相同的两个向量是相等向量，故 C 错误；方向相同或相反的两个非零向量是共线向量，故 D 错误． 答案： B 向量的线性运算 ____________________[ 通关方略 ]____________________ 1 ．两个向量的和仍是一个向量． 2 ．利用三角形法则进行加法运算时，两向量要首尾相连，和向量由第一个向量的起点指向第二个向量的终点 ( 可结合物理中位移的合成来认识 ) ；利用平行四边形法则进行加法运算时，两向量要有相同的起点 ( 可结合物理中力的合成来认识． ) 3 ．当两个向量共线时，三角形法则仍适用，而平行四边形法则不适用． 4 ．利用三角形法则进行减法运算时，两个向量要有相同的起点，然后连接两向量的终点，并指向被减向量即为差向量． 5 ．实数和向量可以求积，但不能求和或求差． 6 ． λ ＝ 0 或 a ＝ 0 ⇔ λ a ＝ 0 . 答案： A 共线向量定理 共线向量定理：向量 a ( a ≠ 0) 与 b 共线，当且仅当有唯一一个实数 λ ，使得 . b ＝ λ a 5 ．设 a 与 b 是两个不共线向量，且向量 a ＋ λ b 与 2 a － b 共线，则 λ ＝ ________. 平面向量的有关概念 [ 答案 ] 　 2 反思总结 1 ． 判断两向量的关系时，特别注意以下两种特殊情况 (1) 零向量的方向及与其他向量的关系； (2) 单位向量的长度及方向． 2 ．向量不能比较大小，但它们的模可以比较大小． 3 ．注意区分向量共线与向量所在的直线平行间的关系． 变式训练 1 ．给出下列命题： ① 两个具有公共终点的向量，一定是共线向量． ② 两个向量不能比较大小，但它们的模能比较大小． ③ λ a ＝ 0( λ 为实数 ) ，则 λ 必为零． ④ λ ， μ 为实数，若 λ a ＝ μ b ，则 a 与 b 共线． 其中错误命题的个数为 ( 　　 ) A ． 1 　　　　 B ． 2 　　　　 C ． 3 　　　　 D ． 4 解析： ① 错，由于终点相同，两起点不一定相同，所以可以不共线． ② 对，由于模是实数，所以可以比较大小． ③ 错，由于 a ＝ 0 ， λ ≠ 0 时，也可以得 λ a ＝ 0. ④ 错，由于 λ ＝ μ ＝ 0 时，虽然 λ a ＝ μ b ，则 a 与 b 可以不共线， ∴ 错误命题个数为 3. 答案： C 向量的线性运算 反思总结 进行向量运算时，要尽可能地将它们转化到平行四边形或三角形中，充分利用相等向量、相反向量、三角形的中位线定理、相似多边形对应边成比例等性质，把未知向量用已知向量表示出来． 共线向量 反思总结 1 ． 向量共线的充要条件中要注意当两向量共线时，通常只有非零向量才能表示与之共线的其他向量，要注意待定系数法和方程思想的运用． 2 ．证明三点共线问题，可用向量共线来解决，但应注意向量共线与三点共线的区别与联系，当两向量共线且有公共点时，才能得出三点共线． 变式训练 2 ．设 a ， b 是两个非零向量，则下列选项正确的是 ( 　　 ) A ．若 | a － b | ＝ | a | － | b | ，则 a ⊥ b B ．若 a ⊥ b ，则 | a － b | ＝ | a | ＋ | b | C ．若 | a － b | ＝ | a | － | b | ，则 a ， b 共线 D ．若 a ， b 平行，则 | a ＋ b | ＝ | a | ＋ | b | 解析： 若 | a － b | ＝ | a | － | b | ，则 a ， b 共线， ∴ 选项 A 是错误的．若 a ⊥ b ，则以 a ， b 为邻边构成的长方形的对角线的长不可能等于两个邻边长的和， ∴ 选项 B 是错误的．若 a ， b 平行，则 a ， b 的方向可能相同，也可能相反，如果 a ， b 的方向相反，则 | a － b | ＝ | a | ＋ | b | ， ∴ 选项 D 是错误的． 答案： C —— 以向量为背景的新定义问题 ) 向量具有几何和代数的双重特征，因此它具有很强的延伸性，在各种考题中常常会出现以向量为背景的新定义问题．此类问题一般结合向量知识给出一些新定义、新信息，然后让考生利用这些新定义、新信息以及所学的知识来解题． 由题悟道 本题以共线向量为背景，结合不等式，通过创新情境，考查化归与转化思想，在整个解题过程中所给的定义是解题的重要依据和方法． 答案： D 本小节结束 请按 ESC 键返回