高考理科数学复习练习作业83 10页

题组层级快练(八十三)‎ ‎1．(2014·新课标全国Ⅱ理)某地区空气质量监测资料表明，一天的空气质量为优良的概率是0.75，连续两天为优良的概率是0.6，已知某天的空气质量为优良，则随后一天的空气质量为优良的概率是(　　)‎ A．0.8　　　　　　　　 B．0.75‎ C．0.6 D．0.45‎ 答案　A 解析　根据条件概率公式，直接代入，可求得随后一天的空气质量为优良的概率．已知连续两天为优良的概率是0.6，那么在前一天空气质量为优良的前提下，要求随后一天的空气质量为优良的概率，可根据条件概率公式，得P＝＝0.8.‎ ‎2．某厂大量生产某种小零件，经抽样检验知道其次品率是1%，现把这种零件每6件装成一盒，那么每盒中恰好含一件次品的概率是(　　)‎ A．()6 B．0.01‎ C.(1－)5 D．C62()2(1－)4‎ 答案　C 解析　P＝C61·1%·(1－)5.‎ ‎3．箱子里有5个黑球，4个白球，每次随机取出一个球，若取出黑球，则放回箱中，重新取球；若取出白球，则停止取球，那么在第4次取球之后停止的概率为(　　)‎ A. B.× C.× D．C41×× 答案　B 解析　由题意知，第四次取球后停止是当且仅当前三次取的球是黑球，第四次取的球是白球的情况，此事件发生的概率为×.‎ ‎4．(2017·沧州七校联考)某道路的A，B，C三处设有交通灯，这三盏灯在一分钟内开放绿灯的时间分别为25秒，35秒，45秒．某辆车在这条路上行驶时，三处都不停车的概率是(　　)‎ A. B. C. D. 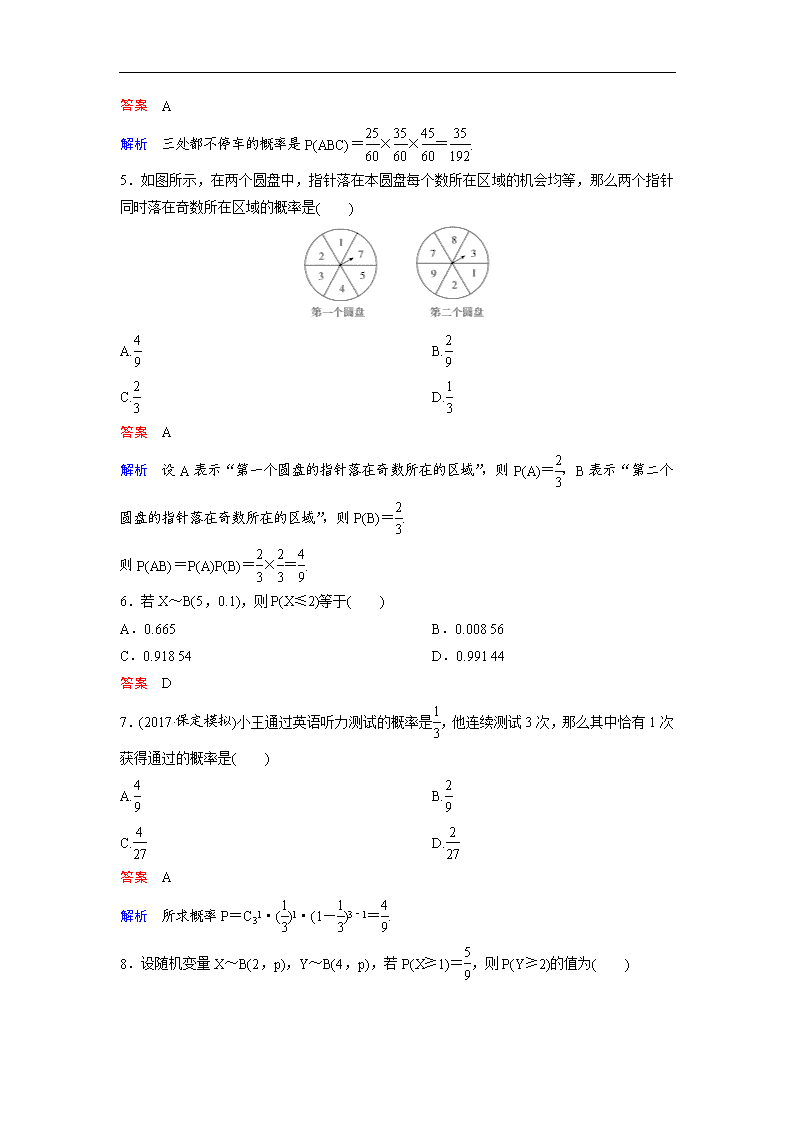答案　A 解析　三处都不停车的概率是P(ABC)＝××＝.‎ ‎5．如图所示，在两个圆盘中，指针落在本圆盘每个数所在区域的机会均等，那么两个指针同时落在奇数所在区域的概率是(　　)‎ A. B. C. D. 答案　A 解析　设A表示“第一个圆盘的指针落在奇数所在的区域”，则P(A)＝，B表示“第二个圆盘的指针落在奇数所在的区域”，则P(B)＝.‎ 则P(AB)＝P(A)P(B)＝×＝.‎ ‎6．若X～B(5，0.1)，则P(X≤2)等于(　　)‎ A．0.665 B．0.008 56‎ C．0.918 54 D．0.991 44‎ 答案　D ‎7．(2017·保定模拟)小王通过英语听力测试的概率是，他连续测试3次，那么其中恰有1次获得通过的概率是(　　)‎ A. B. C. D. 答案　A 解析　所求概率P＝C31·()1·(1－)3－1＝.‎ ‎8．设随机变量X～B(2，p)，Y～B(4，p)，若P(X≥1)＝，则P(Y≥2)的值为(　　)‎ A. B. C. D. 答案　B 解析　P(X≥1)＝P(X＝1)＋P(X＝2)＝C21p(1－p)＋C22p2＝，解得p＝.(0≤p≤1，故p＝舍去)．‎ 故P(Y≥2)＝1－P(Y＝0)－P(Y＝1)＝1－C40×()4－C41××()3＝.‎ ‎9．口袋里放有大小相等的两个红球和一个白球，有放回地每次摸取一个球，定义数列{an}：an＝ 如果Sn为数列{an}的前n项和，那么S7＝3的概率为(　　)‎ A．C75· B．C72· C．C74· D．C73· 答案　B 解析　S7＝3说明摸取2个红球，5个白球，故S7＝3的概率为C72·.‎ ‎10．(2017·山东师大附中模拟)已知某次考试中一份试卷由5个选择题和3个填空题组成，每个选择题有4个选项，其中有且仅有1个选项是正确的．已知每题答案正确得5分，答案错误得0分，满分40分．若小强做对任一个选择题的概率为，做对任一个填空题的概率为，则他在这次考试中得分为35分的概率为(　　)‎ A. B. C. D. 答案　A 解析　设小强做对选择题的个数为ξ，做对填空题的个数为η，则ξ～B(5，)，η～B(3，)，由于每题答案正确得5分，答案错误得0分，若小强得分为35分，则他做对题的个数为7，故所求概率为P(ξ＝5)P(η＝2)＋P(ξ＝4)P(η＝3)＝C55()5×C32()2(1－)＋C54()4(1－)×C33()3＝.‎ ‎11．(2017·上海十二校联考)小李同学在上学路上要经过4个路口，假设在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是，则他在上学路上到第三个路口时首次遇到红灯的概率为________．(用最简分数表示)‎ 答案　 解析　由于在各路口是否遇到红灯是相互独立的，遇到红灯的概率都是，则第三个路口首次遇到红灯的概率为P＝(1－)×(1－)×＝.‎ ‎12．(2017·天津一中期末)将一个半径适当的小球放入如图所示的容器最上方的入口处，小球将自由下落．小球在下落的过程中，将3次遇到黑色障碍物，最后落入A袋或B袋中．已知小球每次遇到黑色障碍物时，向左、右两边下落的概率都是，则小球落入A袋中的概率为________．‎ 答案　 解析　记“小球落入A袋中”为事件A，“小球落入B袋中”为事件B，则事件A的对立事件为B，若小球落入B袋中，则小球必须一直向左落下或一直向右落下，故P(B)＝()3＋()3＝，从而P(A)＝1－P(B)＝1－＝.‎ ‎13．某大厦的一部电梯从底层出发后只能在第18，19，20层停靠．若该电梯在底层载有5位乘客，且每位乘客在这三层的每一层下电梯的概率均为，用ξ表示这5位乘客在第20层下电梯的人数，则P(ξ＝4)＝________．‎ 答案　 解析　考查一位乘客是否在第20层下电梯为一次试验，这是5次独立重复试验，故ξ～B(5，)．即有P(ξ＝k)＝C5k()k×()5－k，k＝0，1，2，3，4，5.‎ ‎∴P(ξ＝4)＝C54()4×()1＝.‎ ‎14．某次知识竞赛规则如下：在主办方预设的5个问题中，选手若能连续正确回答出两个问题，即停止答题，晋级下一轮．假设某选手正确回答每个问题的概率都是0.8，且每个问题的回答结果相互独立，则该选手恰好回答了4个问题就晋级下一轮的概率等于________．‎ 答案　0.128‎ 解析　依题意得，事件“该选手恰好回答了4个问题就晋级下一轮”即意味着“‎ 该选手在回答前面4个问题的过程中，要么第一个问题答对且第二个问题答错，第三、四个问题都答对了；要么第一、二个问题都答错；第三、四个问题都答对了”，因此所求事件的概率等于[0.8×(1－0.8)＋(1－0.8)2]×0.82＝0.128.‎ ‎15．(2017·武汉调研)如图所示，圆通快递公司送货员从公司A处准备开车送货到某单位B处，有A→C→D→B，A→E→F→B两条路线．若该地各路段发生堵车与否是相互独立的，且各路段发生堵车事件的概率如图所示(例如A→C→D算作两个路段，路段AC发生堵车事件的概率为，路段CD发生堵车事件的概率为)．若使途中发生堵车事件的概率较小，则由A到B应选择的路线是________．‎ 思路　利用相互独立事件同时发生的概率公式与对立事件的概率公式、求出路线A→C→D→B途中堵车与路线A→E→F→B途中堵车的概率，哪条路线堵车的概率小，就选择哪条路线．‎ 答案　A→E→F→B 解析　路线A→C→D→B途中发生堵车事件的概率为P1＝1－(1－)×(1－)×(1－)＝，‎ 路线A→E→F→B途中发生堵车事件的概率为P2＝1－(1－)×(1－)×(1－)＝.‎ 因为<，所以应选择路线A→E→F→B.‎ ‎16．某次知识竞赛中，从6道备选题中一次性随机抽取3道，并独立完成所抽取的3道题．甲选手能正确完成其中4道题；乙选手能正确完成每道题的概率都为，且每道题正确完成与否互不影响．规定至少正确答对其中2道题目便可过关．‎ ‎(1)求甲选手能晋级的概率；‎ ‎(2)记所抽取的3道题中，甲选手答对的题目数为ξ，写出ξ的概率分布，并求E(ξ)；‎ ‎(3)乙选手能答对的题目数为η，求η的概率分布与D(η)．‎ 答案　(1)　(2)2　(3) 解析　(1)记甲选手能晋级为事件A，则基本事件总数n＝C63＝20，‎ 事件A包含的基本事件数m＝C43＋C42C21＝16，所以P(A)＝＝.‎ ‎(2)ξ的所有可能取值为1，2，3.‎ P(ξ＝1)＝＝，P(ξ＝2)＝＝，P(ξ＝3)＝＝.‎ 则ξ的分布列为 ξ ‎1‎ ‎2‎ ‎3‎ P 所以E(ξ)＝1×＋2×＋3×＝2.‎ ‎(3)依题意知，η服从B(3，)．‎ P(η＝k)＝C3k()k(1－)3－k，k＝0，1，2，3.‎ 即P(η＝0)＝C30()0()3＝，P(η＝1)＝C31·()1()2＝，P(η＝2)＝C32·()2·()1＝，‎ P(η＝3)＝C33()3·()0＝.‎ 则η的分布列为 η ‎0‎ ‎1‎ ‎2‎ ‎3‎ P 所以D(η)＝3××＝.‎ ‎17．在某校老师趣味投蓝比赛中，比赛规则是：每场投6个球，至少投进4个球且最后2个球都投进者获奖；否则不获奖．已知教师甲投进每个球的概率都是.‎ ‎(1)记教师甲在每场的6次投球中投进球的个数为X，求X的分布列及数学期望；‎ ‎(2)求教师甲在一场比赛中获奖的概率．‎ 答案　(1)E(X)＝4　(2) 解析　(1)X的所有可能取值为0，1，2，3，4，5，6.‎ 依条件可知，X～B(6，)，P(X＝k)＝C6k·()k·()6－k(k＝0，1，2，3，4，5，6)．‎ 所以X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ P 故E(X)＝(0×1＋1×12＋2×60＋3×160＋4×240＋5×192＋6×64)＝＝4.‎ ‎(或因为X～B(6，)，所以E(X)＝6×＝4.)‎ ‎(2)设教师甲在一场比赛中获奖为事件A，‎ 则P(A)＝C42·()2·()4＋C41··()5＋()6＝，‎ 即教师甲在一场比赛中获奖的概率为.‎ ‎1．(2017·洛阳模拟)在某次人才招聘会上，假定某毕业生赢得甲公司面试机会的概率为，赢得乙、丙两公司面试机会的概率均为，且三个公司是否让其面试是相互独立的．则该毕业生只赢得甲、乙两个公司面试机会的概率为(　　)‎ A. B. C. D. 答案　B 解析　记事件A为“该毕业生赢得甲公司的面试机会”，事件B为“该毕业生赢得乙公司的面试机会”，事件C为“该毕业生赢得丙公司的面试机会”．‎ 由题可得P(A)＝，P(B)＝P(C)＝.‎ 则事件“该毕业生只赢得甲、乙两个公司面试机会”为ABC，‎ 由相互独立事件同时成立的概率公式，可得 P(ABC)＝P(A)P(B)P(C)＝××(1－)＝，故选B.‎ 回顾　求解此类相互独立事件题需“双会”：一是会用相互独立事件同时发生的概率公式，即事件A，B为相互独立事件，则事件A，B同时发生的概率为P(AB)＝P(A)P(B)；二是会用对立事件的概率公式，遇到事件较为复杂[含“至多”“至少”等词的事件]时，常将事件转化，借助对立事件来解决，可加快解题速度．‎ ‎2．(2017·长沙调研)某次数学摸底考试共有10道选择题，每道题给的四个选项中有且只有一个选项是正确的；张三同学每道题都随意地从中选了一个答案，记该同学至少答对9道题的概率为P，则下列数据中与P的值最接近的是(　　)‎ A．3×10－4 B．3×10－5‎ C．3×10－6 D．3×10－7‎ 思路　由“随意”两字知道这是个独立重复试验问题．‎ 答案　B 解析　由题意知本题是一个独立重复试验，试验发生的次数是10，选题正确的概率是，该同学至少答对9道题包括答对9道题或答对10道题，‎ 根据独立重复试验的公式得到该同学至少答对9道题的概率为P＝C109·()9×＋C1010()10≈3×10－5.‎ ‎3．如果ξ～B，那么使P(ξ＝k)取最大值的k值为(　　)‎ A．3 B．4‎ C．5 D．3或4‎ 答案　D 解析　采取特殊值法．‎ ‎∵P(ξ＝3)＝C153，P(ξ＝4)＝C154，P(ξ＝5)＝C155，‎ 从而易知P(ξ＝3)＝P(ξ＝4)>P(ξ＝5)．故选D.‎ ‎4.如图所示，用K，A1，A2三类不同的元件连接成一个系统．当K正常工作且A1，A2至少有一个正常工作时，系统正常工作，已知K，A1，A2正常工作的概率依次是0.9，0.8，0.8，则系统正常工作的概率为(　　)‎ A．0.960 B．0.864‎ C．0.720 D．0.576‎ 答案　B 解析　A1，A2不能同时工作的概率为0.2×0.2＝0.04，所以A1，A2至少有一个正常工作的概率为1－0.04＝0.96，所以系统正常工作的概率为0.9×0.96＝0.864.‎ ‎5．由0，1组成的三位编号中，若用A表示“第二位数字为0的事件”，用B表示“第一位数字为0的事件”，则P(A|B)＝(　　)‎ A. B. C. D. 答案　A 解析　因为第一位数字可为0或1，所以第一位数字为0的概率P(B)＝，第一位数字为0且第二位数字也是0，即事件A，B同时发生的概率P(AB)＝×＝，所以P(A|B)＝＝＝.‎ ‎6．在4次独立重复试验中事件A出现的概率相同，若事件A至少发生一次的概率为，则事件A在1次试验中出现的概率为________．‎ 答案　 解析　A至少发生一次的概率为，事件A都不发生的概率为1－＝＝()4，所以A在一次试验中出现的概率为1－＝.‎ ‎7．在4次独立重复试验中，随机事件A恰好发生1次的概率不大于其恰好发生2次的概率，则事件A在一次试验中发生的概率p的取值范围是(　　)‎ A．[0.4，1) B．(0，0.6]‎ C．(0，0.4] D．[0.6，1)‎ 答案　A 解析　C41p(1－p)3≤C42p2(1－p)2，4(1－p)≤6p，p≥0.4，又0