七年级下数学课件《乘法公式》课件2_苏科版 26页

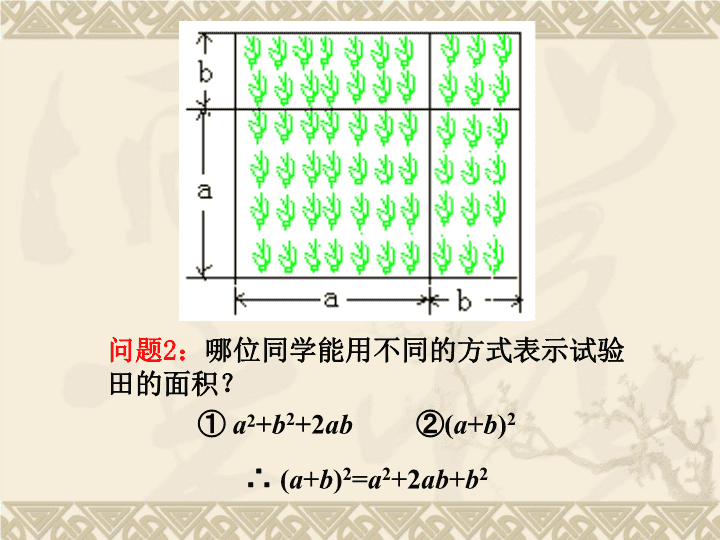
乘法公式 去年，一位农民在一次“科技下乡”活 动中得到启示，将一块边长为a米的正方形 农田改成试验田，种上了优质的杂交水稻， 一年来，收益很大，今年，又一次“科技下 乡”活动，使老农铁了心，要走科技兴农的 路子，于是他想把原来的试验田，边长增加 b米，形成四块试验田，种植不同的新品种. 问题1：同学们，谁来帮老爷爷实现这个愿 望呢？ 问题2：哪位同学能用不同的方式表示试验 田的面积？ ① a2+b2+2ab ②(a+b)2 ∴ (a+b)2=a2+2ab+b2 完全平方公式的数学表达式： 完全平方公式的文字叙述： 你能根据图1和图2中的面积说 明完全平方公式吗？ b a a b b a b a 图 1 图2 思考: b ba a  2)( ba (a+b)² a² 2a b² 2b ab ab ab2+ + 和的完全平方公式： 完全平方公式 的几何意义 a a b b (a-b)²  2)( ba 2a ab 2 22a ab b   a² ab ab ab 2b b² 差的完全平方公式： 完全平方公式 的几何意义 公式特征： 4、公式中的字母a，b可以表示数、单项 式和多项式. 1、积为二次三项式； 2、积中两项为两数的平方和； 3、另一项是两数积的2倍，且与乘式中 间的符号相同. 首平方，尾平方， 积的2倍放中央 . 下面各式的计算是否正确？如果不正确， 应当怎样改正？ (⑴)(x+y)2=x2 +y2 (2)(x-y)2 =x2 -y2 (3) (-x+y)2 =x2+2xy+y2 (4) (2x+y)2 =4x2 +2xy +y2 (x+y)2 =x2+2xy+y2 (x-y)2 =x2 -2xy+y2 想一想: 例1 计算：（a-b）2 解：   .2 2 22 22 2 2 baba bbaa ba ba     ）-（）-（ ）-（ ）（ 思考 (a+b)2与(-a-b)2相等吗？ (a-b)2与(b-a)2相等吗？ (a-b)2与a2-b2相等吗？ 为什么？ 例2 用完全平方式计算： 解： ； ）（ ））（（ 2 22 2 93025 33525 351 pp pp p    .523 722351 2 22 ）-）（（ ；））（（；））（（   a yxp ； ）（）（ ））（（ 22 22 2 49284 77222 722 yxyx yyxx yx    .25204 55222 523 2 22 2    aa aa a ）-（）-（）-（）（ ）-）（（ 1、运用完全平方公式计算： 解: (4m+n)2= =16m2 (1)(4m+n)2 (4m)2+2·(4m)·n +n2 +8mn +n2 解： (x-2y)2= =x2 (2)(x-2y)2 x2 -2·x·2y +(2y)2 -4xy +4y2 (1) 1022 解： 1022 = (100+2)2 =10000+400+4 =10404. (2) 992 解： 992 = (100 –1)2 =10000 -200+1 =9801. 2、运用完全平方公式计算： ( ) ( )( ) ( ) ( )( ) ( ) ( )( ) 1 2 2 2 3 3 3 2 2 a a x x m n m n       2 4a  29 x  2 24m n  观察等式 比较等号两边的式子，等号 的左边有什么特征？等号的 右边有什么特征？ 2 22a  2 23 x  ( )2 22m n  大胆猜想 ( )( ) __________a b a b   2 2a b 两数和 两数差 两数平方差 两数和与这两数差的积等 于这两数的平方差. 平 方 差 公 式 概括总结 2 2( )( )a b a b a b    （2）等号右边是这两 个数(字母)的平方差. 平方差公式的特征： （1）等号左边是两个 数(字母)的和乘以这两 个数(字母)的差. 注：必须符合平方差 公式特征的代数式才能 用平方差公式. 公式中的字母的意义很 广泛，可以代表常数， 单项式或多项式 . 平方差公式： 下图是一个边长为 a 的大正方形，割 去一个边长为b 的小正方形.小明将绿色 和黄色两部分拼成一个长方形. 问:小明能拼成功吗？ 做一做 b a a b 例3 用平方差公式计算： 解： .222551 ））（）（（）；）（）（（ mnnmyxyx  ； ）（ ））（）（（ 22 22 25 5 551 yx yx yxyx    .4 2 22 222 22 22 mn mn mnmn mnnm     ）（ ））（（ ））（）（（ 原图实际面积为：________________ 长方形的面积为：_________________ 2 2a b ( )( )a b a b  b a a b a-b b b a b ( )( ) 2 2a b a b a b    解决问题 ( )( ) 2 2a b a b a b   练一练 阅读算式，按要求填写下面的表格 2m3n (-2m+3n)(2m+3n) 3x2(2-3x)(2+3x) 5x(x+5)(x-5) 写成“a2-b2” 的形式 与平方差 公式中b 对应的项 与平方差 公式中a 对应的项 算式 2 25x   222 3x (3n)²-(2m)² 拓展练习: 1. =____； 2.若 是一个完全平方公式， 则 _______； 22 20092009200822008  922  kxx k 3.若 是一个完全平方公式， 则 _______； k 22 8 kxx  1 3 4 运用平方差公式计算: (2)    1 1( )( ) 2 2 b a b a (1) ( 2 3 )( 2 3 )a b a b  练一练 1 1 2 4 x y x y             ( ) ( )( ) ( ) ( )( ) ( ) ( )( ) ( ) ( )( ) ( ) 1 2 2 2 3 2 3 2 3 4 3 4 3 4 1 1 5 a a a b a b k k x x            能 力 提 高 ( ) ( )( ) ( ) ( )( ) ( ) ( )( ) 2 2 2 2 2 2 1 3 5 9 25 2 3 5 9 25 3 5 3 9 25 x y x y x y x y y x x y           3 5x y 5 3y x  3 5x y 