七年级数学下册第6章一元一次方程6-2解一元一次方程2解一元一次方程第2课时教学课件华东师大版 25页

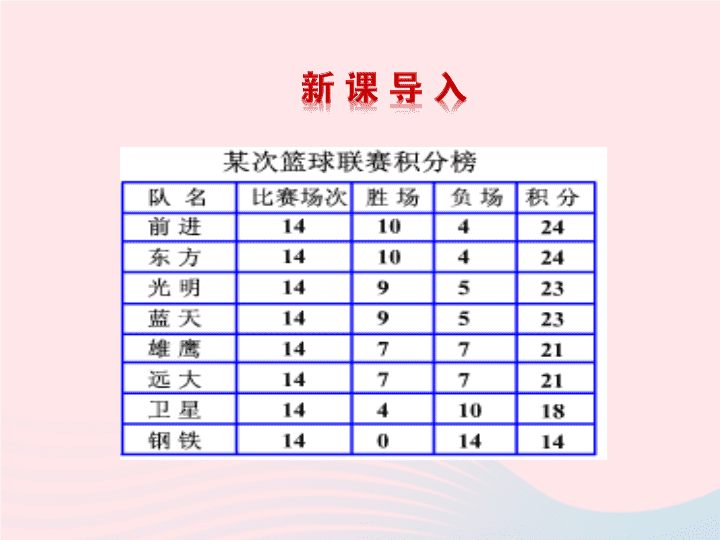
2 解一元一次方程 第2课时 1. 掌握一元一次方程解决实际问题的步骤 . 2. 能利用一元一次方程解决实际问题 . 问题 1 ：通过观察积分榜，你能选择出其中哪一行最能说 明负一场积几分吗？进而你能得到胜一场积几分吗？ 从最下面一行数据可以看出：负一场积 1 分 , 设胜一场积 x 分，从第一行列方程 10x ＋ 4 ＝ 24 ． 由此得 x ＝ 2 ． 即：负一场积 1 分，胜一场积 2 分． 问题 2 ：用式子表示总积分与胜、负场数之间的数量关系 . 如果一个队胜 m 场，则负（ 14 － m ）场，胜场积分 2m 分，负场积分（ 14 － m ）分，总积分为 : 2m ＋（ 14 － m ）＝ m ＋ 14 ． 问题 3 ：某队的胜场总积分能等于它的负场总积分吗？ 设一个队胜了 x 场，则负了（ 14 － x ）场． 如果这个队的胜场总积分等于负场总积分， 则得方程 2x －（ 14 － x ）＝ 0, 由此得 因此没有哪个队的胜场总积分等于负场总积分． 用一元一次方程解决实际问题，需要思考： 1. 题目中的已知量是什么？未知量是什么？ 2. 题目中的等量关系是什么？ 【 例 1】 某文艺团体为“希望工程”募捐组织了一次义 演，售出 1 000 张票，筹得票款 6 950 元 . 学生票 5 元 / 张， 成人票 8 元 / 张 . 问：售出成人和学生票各多少张？ 问题一：上面的问题中包含哪些等量关系？ 成人票数 + 学生票数 =1 000 张 （ 1 ） 成人票款 + 学生票款 =6 950 元 （ 2 ） 【 例题 】 问题三： 列方程解应用题，并考虑还有没有其他的解题方法？ 问题二：设售出的学生票为 x 张，填写下表 学 生 成 人 票数 / 张 票款 / 元 x 1 000-x 5x 8(1 000-x) 【 解析 】 方法一： 设售出学生票为 x 张，则成人票为（ 1 000-x ）张 , 由题意得： 5x+8(1 000-x)=6 950 5x+8 000-8x=6 950 5x-8x=6 950-8 000 -3x=-1 050 x=350. 1 000-350=650 （张） . 答：售出学生票 350 张，成人票 650 张 . 方法二： 设所得学生票款为 y 元，填写下表 学 生 成 人 票款 / 元 票数 / 张 y/5 (6 950-y)/8 y 6 950-y 等量关系：成人票数 + 学生票数 =1 000 张 ，列方程得： y/5+ (6 950-y)/8=1 000 解方程 8y+5(6 950-y)=40 000 8y+34 750-5y=40 000 3y=5 250 y=1 750, 1 750/5=350 （张） , 1 000-350=650 （张） . 答：售出学生票 350 张，成人票 650 张 . 如果票价不变，那么售出 1 000 张票所得票款可能是 6 930 元 吗？为什么？ 【 解析 】 设售出的学生票为 x 张，则由题意得： 8 （ 1 000-x ） +5x=6 930 ， 解得 x=1 070/3. 因为票的张数不可能出现分数，所以不可能 . 结论： 在实际问题中，方程的解是有实际意义的，因此 应将解代入原方程看是否符合题意 . 想一想 一班有 40 位同学 , 新年时开晚会 , 班主任到超市花了 115 元 买果冻与巧克力共 40 个 , 若果冻每 2 个 5 元，巧克力每块 3 元 , 问班主任分别买了多少果冻和巧克力 ? 【 解析 】 因为 果冻每 2 个 5 元，所以果冻每个 2.5 元 . 设班主任买了 x 个果冻，则买（ 40-x ）块巧克力，可列方 程为 2.5x+ （ 40-x)×3=115, 解得 x=10 ，所以 40-x=40-10=30. 答：班主任买了 10 个果冻，买了 30 块巧克力 . 【 跟踪训练 】 【 例 2】 小明和小彬每天早晨坚持跑步，小彬每秒跑 4 米， 小明每秒跑 6 米 . （ 1 ）如果他们站在百米跑道的两端同时相向起跑，那么 几秒后两人相遇？ （ 2 ）如果小明站在百米跑道的起跑处，小彬站在他前面 10 米处，两人同时同向起跑，几秒后小明能追上小彬？ 【 例题 】 趣味图解： (1) 如果他们站在百米跑道的两端同时相向起跑，那么几 秒后两人相遇？ 小明所跑的路程 小彬所跑的路程 + =100 小明所跑的路程 小彬所跑的路程 小明 小彬 100 米 相遇 6x 10 4x 若设ｘ秒后小明能追上小彬 . 小明 小彬 小明 小彬 追及点 追及点 趣味图解： （ 2 ）如果小明站在百米跑道的起跑处，小彬站在他前面 10 米处，两人同时同向起跑，几秒后小明能追上小彬？ 【 解析 】 （ 1 ）设 x 秒后两人相遇 . 由题意得 4x+6x=100, 10x=100, x=10. 答： 10 秒后两人相遇 . （ 2 ）设 x 秒后小明追上小彬， 由题意得 6x-4x=10 ， 2x=10 ， x=5. 答： 5 秒后小明追上小彬 . 甲乙两人赛跑，甲的速度是 8 米 / 秒，乙的速度是 5 米 / 秒，如果甲从起点处往后退 20 米，乙从起点处向前进 10 米，问甲经过几秒钟追上乙？ 【 解析 】 设甲经过 x 秒追上乙，根据题意，得 8x-5x=20+10 ， 解得 x=10. 答：甲经过 10 秒钟追上乙 . 【 跟踪训练 】 1. 甲、乙两人都从某地出发到学校，甲每小时步行 5 千 米，先出发 1.5 小时，乙骑自行车，乙出发 50 分钟后，两 人同时到达学校，则乙骑自行车的速度为每小时（ ） A.12 千米 B.13 千米 C.14 千米 D.15 千米 【 解析 】 选 C. 设乙骑自行车的速度为每小时 x 千米，根 据甲步行走的路程 = 乙骑自行车走的路程，列方程为 （ 1.5+ ） ×5= x ，解得 x=14 （千米 / 小时） . 2. （潜江 · 中考）元代朱世杰所著的 《 算学启蒙 》 里有这 样一道题：“良马日行二百四十里，驽马日行一百五十 里，驽马先行一十二日，问良马几何追及之？”请你回答： 良马 ______ 天可以追上驽马 . 【 解析 】 设良马 x 天可以追上驽马，根据相等关系：驽马 先行一十二日的路程 + 驽马 x 天行的路程 = 良马 x 天行的路 程，可列方程 12×150+150x=240x ，解得 x=20. 答案： 20 【 解析 】 选 B. 设需更换的新型节能灯有 x 盏，根据题 意 ,70× （ x-1 ） = （ 106-1 ） ×36 ，解得 x=55. 3. （日照 · 中考）某道路一侧原有路灯 106 盏，相邻两盏 灯的距离为 36 米，现计划全部更换为新型的节能灯，且 相邻两盏灯的距离变为 70 米，则需更换的新型节能灯有 ( ) A.54 盏 B.55 盏 C.56 盏 D.57 盏 4. （眉山 · 中考）某渔场计划购买甲、乙两种鱼苗共 6 000 尾，甲种鱼苗每尾 0.5 元，乙种鱼苗每尾 0.8 元．相关资料表 明：甲、乙两种鱼苗的成活率分别为 90% 和 95% ．若购买这批 鱼苗共用了 3 600 元，求甲、乙两种鱼苗各购买了多少尾？ 【 解析 】 设购买甲种鱼苗 x 尾，则购买乙种鱼苗 （ 6 000-x ）尾，根据题意，得 0.5x+0.8(6 000-x)=3 600 ， 解这个方程，得： x=4 000, 所以 6 000-x=2 000. 答：甲种鱼苗买 4 000 尾，乙种鱼苗买 2 000 尾． 5. 我区某学校原计划向内蒙古察右后旗地区的学生捐赠 3 500 册图书 , 实际共捐赠了 4 125 册，其中初中学生捐赠了 原计划的 120%, 高中学生捐赠了原计划的 115%. 问 : 初中学 生和高中学生原计划各捐赠图书多少册 ? 【 解析 】 设初中学生原计划捐赠图书 x 册，则高中学生原 计划捐赠图书（ 3 500-x ）册，根据题意，得 120%x+(3 500-x)×115%=4 125, 解得 x=2 000 ，所以 3 500-x=1 500. 答：初中学生原计划捐赠图书 2 000 册，高中学生原计划 捐赠图书 1 500 册 . 用一元一次方程解决实际问题的一般步骤： 实际问题 数学问题 已知量、未知量、 等量关系 方程 方程 的解 解的 合理性 解释 抽象 分析 列出 求出 验证 合理 不合理 通过本课时的学习，需要我们掌握： 再长的路，一步步也能走完，再短的路，不迈开双脚也无法到达 .