最新人教版七年级数学下册精品课件第五章 相交线与平行线 小结与复习 18页

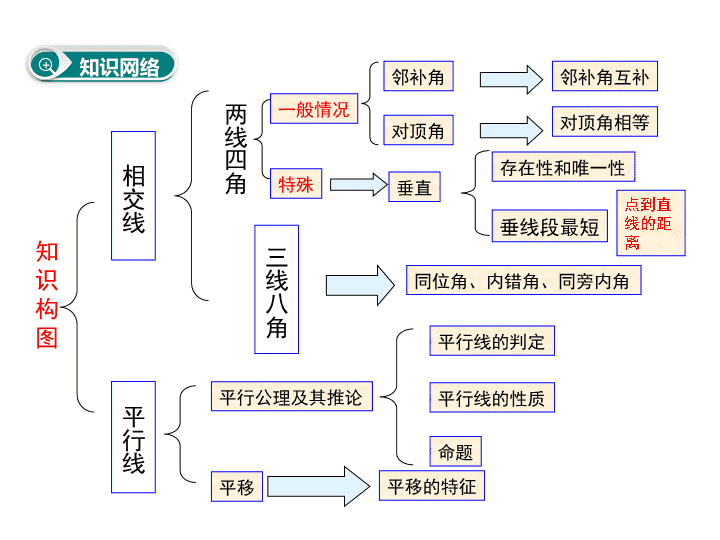
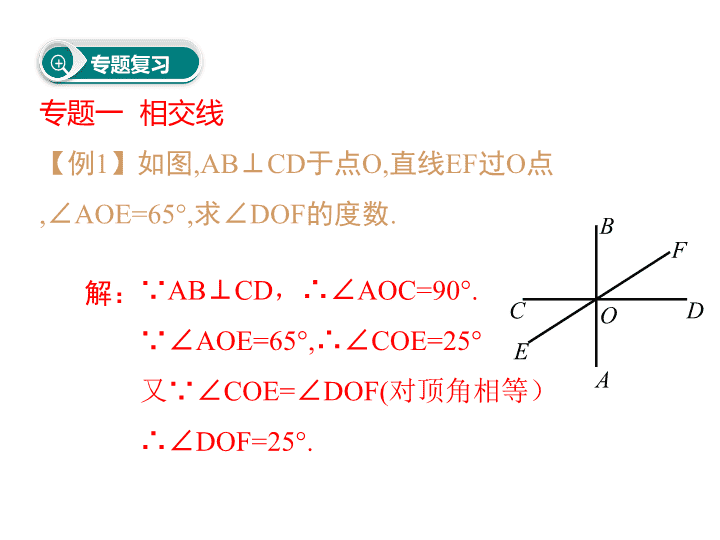
小结与复习 知识网络 专题复习 课堂小结 课后训练 第五章 相交线与平行线 知识网络 相 交 线 一般情况 邻补角 对顶角 邻补角互补 对顶角相等 特殊 垂直 存在性和唯一性 垂线段最短 点到直 线的距 离 同位角、内错角、同旁内角 平 行 线 平行公理及其推论 平行线的判定 平行线的性质 平移 平移的特征 命题 知 识 构 图 两 线 四 角 三 线 八 角 专题复习 【例1】如图,AB⊥CD于点O,直线EF过O 点,∠AOE=65°,求∠DOF的度数. B A C D F E O 解：∵AB⊥CD，∴∠AOC=90°. ∵∠AOE=65°,∴∠COE=25° 又∵∠COE=∠DOF(对顶角相等） ∴∠DOF=25°. 专题一 相交线 【迁移应用1】如图,AB,CD相交于点 O,∠AOC=70°,EF平分∠COB,求∠COE的度数. A B C D E F O 答案：∠COE=125°. 【归纳拓展】两条直线相交包括垂直和斜交两种情形. 相交时形成了两对对顶角和四对邻补角.其中垂直是 相交的特殊情况，它将一个周角分成了四个直角. 【例2】如图，AD为三角形ABC的高，能表示点到直 线（线段）的距离的线段有（ ） A.2条 B.3条 C.4条 D.5条 解析：从图中可以看到共有三条，A到BC的垂线 段AD,B到AD的垂线段BD,C到AD的垂线段CD. B CD A 专题二 点到直线的距离 B 【迁移应用2】如图AC⊥BC,CD⊥AB于点D,CD=4.8cm, AC=6cm,BC=8cm,则点C到AB的距离是 cm; 点A到BC的距离是 cm;点B到AC的距离是 cm. 【归纳拓展】点到直线的距离容易和两点之间的距离相 混淆.当图形复杂不容易分析出是哪条线段时，准确掌 握概念，抓住垂直这个关键点，认真分析图形是关键. 4.8 6 8 【例3】(1)如图所示,∠1=72°,∠2=72°,∠3=60°,求 ∠4的度数. 解：∵∠1=∠2=72°， ∴a//b (内错角相等，两直线平行）. ∴∠3+∠4=180°. (两直线平行，同旁内角互补) ∵∠3=60°，∴∠4=120°. ab 专题三 平行线的性质和判定 证明: ∵∠DAC= ∠ACB (已知) ∴ AD//BC(内错角相等,两直线平行) ∵ ∠D+∠DFE=180°(已知) ∴ AD// EF(同旁内角互补,两直线平行) ∴ EF// BC(平行于同一条直线的两条直线互相平行) A B C D E F 【迁移应用3】如图所示，把一张长方形纸片ABCD 沿EF折叠，若∠EFG=50°,求∠DEG的度数. 答案：100°. 【归纳拓展】平行线的性质和判定经常结合使用，由 角之间的关系得出直线平行，进而再得出其他角之间 的关系，或是由直线平行得到角之间的关系，进而再 由角的关系得出其他直线平行. 【例4】如图所示,下列四组图形中,有一组中的两个图 形经过平移其中一个能得到另一个,这组图形是 （ ） 解析：紧扣平移的概念解题. 专题四 平移 D 【迁移应用4】如图所示,△DEF经过平移得到△ABC, 那 么∠C的对应角和ED的对应边分别是 （ ） A.∠F,AC B.∠BOD,BA C.∠F,BA D.∠BOD,AC 【归纳拓展】平移前后的图形形状和大小完全相同， 任何一对对应点连线段平行（或共线）且相等. C 解：设∠1的度数为x°,则∠2的度数为x°, ∠3的度数为8x°,根据题意可得 x°+x°+8x°=180°，解得x=18. 即∠1=∠2=18°， 而∠4=∠1+∠2（对顶角相等）. 故∠4=36°. 【例5】如图所示， 交于点O,∠1=∠2,∠3∶ ∠1 =8∶ 1,求∠4的度数. 1 2 3, ,l l l ）） ） ） 1 23 4 3l 1l 2l 专题五 相交线中的方程思想 O 【迁移应用5】如图所示，直线AB与CD相交于点O, ∠AOC:∠AOD=2:3,求∠BOD的度数. A BC D O答案：72° 【归纳拓展】利用方程解决问题,是几何与代数知识相 结合的一种体现,它可以使解题思路清晰,过程简便.在 有关线段或角的求值问题中它的应用非常广泛. 课堂小结 请同学们总结一下本节课所复习的主要内容 若AB∥CD, 则∠ =∠ . 课后训练 1.如图, 若∠3=∠4，则 ∥ ；AD 1 ⌒⌒ ⌒ ⌒ CD 1 43 2 BC 2 2.如图，∠D=70°，∠C= 110°,∠1=69°，则 ∠B= · B A C E D ⌒ 169° A B 3 2 1 DC BA 3.如图1,已知 AB∥CD, ∠1=30°, ∠2=90°,则∠3= ° 4.如图2,若AE∥CD, ∠EBF=135°,∠BFD=60°,∠D=( ) A.75° B.45° C.30° D.15° F DC EBA 图1 图2 60 D 5. 如图,直线AB、CD相交于O,∠AOC=80°,∠1=30°； 求∠2的度数. A C D E 1 2)) O 答案：50° B G E DC BA N M 6. 如图,已知∠AEM＝∠DGN,则你能说明AB平行于CD吗？ F H 变式：若∠AEM＝∠DGN，EF、GH分别平分∠AEG 和∠CGN，则图中还有平行线吗？ EF∥GH