七年级上数学课件- 1-5-1 乘方 课件_人教新课标 29页

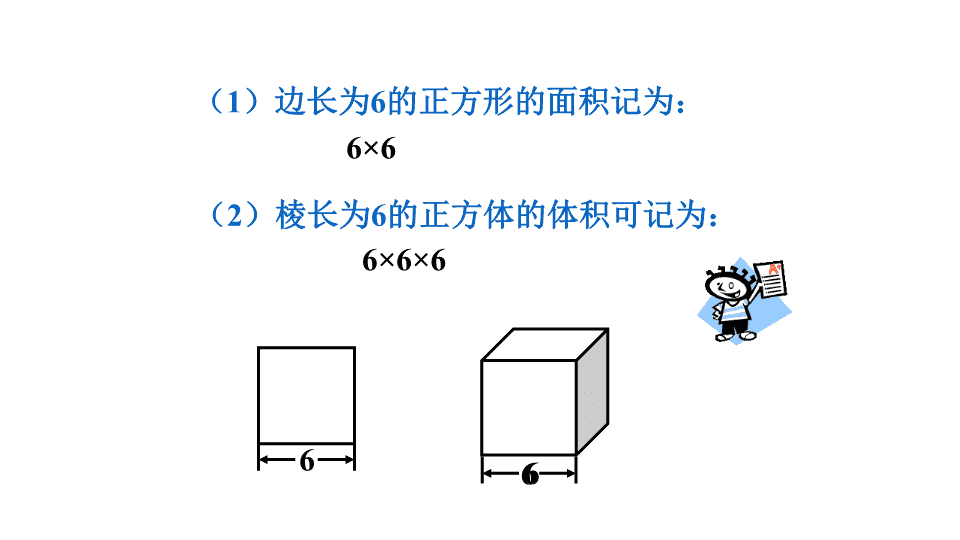
（1）边长为6的正方形的面积记为： （2）棱长为6的正方体的体积可记为： 6×6 6×6×6 6 6 　　若正方形的边长为a,则面积是多少? 　　若正方体的棱长为a，则正方体的体积 为多少? a·a a·a·a a a 细 胞 分 裂 示 意 图 2 2×2 2×2×2 ··· ··· ··· ··· ··· ··· ··· ··· 1个细胞30分钟后分裂成2个， 经过5小时，这种细胞由1个能分裂 成多少个？ 2×2×·······×2×2 10个2 2×2×… ×2×2 10个 记作62，读作6的平方（或二次方）． 6×6 6×6×6 a·a a·a·a 记作210，读作2的10次方. 记作a3，读作a的立方（或三次方）. 记作a2，读作a的平方（或二次方）． 记作63，读作6的立方（或三次方）． 一般地，n个相同因数a相乘，即： 记作：an，读作a的n次方. a×a ×… ×a ×a n个 求n个相同因数a的积的运算叫做乘方. 即：an= a×a ×… ×a ×a n个 an底数 （任意有理数） 指数 幂 an也读作a的n次幂 ． 记作 aa  aaa  aaaa  aaa   n个 记作 3a 记作 记作 a的平方 a的2次幂 a的二次方 a的立方 a的3次幂 a的三次方 a的4次幂 a的四次方 a的n次幂 a的n次方 读作 读作 读作 读作na 4a 2a 　　（1） 34 读做__________，其中底数是 ___，指数是___，表示为___________，结果 为_____. 　　（2） 读做____________，其中底 数是_____，指数是_____，表示为 _________________，结果为______. 33 4        的三次方 3 4   3 4 3的4次幂 3 3×3×3×3 81 3 3 3× × 4 4 4                     27 64 4 3 练一练 一个数可以看作 这个数本身的一次方． a的底数，指数各是多少？ a的底数是a，指数是1． 0的任何次幂等于零; 1的任何次幂等于1． （1）（－5）3 ； （2）（－1）4； （3） ； （4）（－3）5； （5）43 ； （6）34 . 2 1 2       观察各题的结果，你能发现什么规律？ 　　正数的任何次幂是正数； 　　负数的奇次幂是负数， 负数的偶次幂是正数. 计算 ： －125 １ 64 -243 81 1 4 （1）（－1）5＝_________， （2）（－1）8＝_________， （3）12000＝ ____________， （4）02005＝_____________, （5）（－10）4＝_________， （6）（－5）3＝__________. 口算下列各题： －1 1 1 0 10 000 －125 运算名称 运算结果 加法 和 减法 差 乘法 积 除法 商 乘方 幂 与 个 ？那么 与 呢？ 6 3 5 4 1 14 5 4 3             哪一 大 5 4 6 3 4 4 4 4 4 4 1024 5 5 5 5 5 625 1 1 1 1 1 1 1 1 4 4 4 4 4 4 4 4096 1 1 1 1 1 . 3 3 3 3 27                                 ; ; ; 45>54. 6 31 1< . 4 3             　　一个大于1的正数作底数，指 数越大，乘方的结果越大； 　　而一个小于1的正数作底数， 指数越大，乘方的结果就越小 ． 　 3＋52×（－7）这个式子中，存在哪 几种计算？这道题按什么顺序计算？ 存在+、×和乘方的运算．根据前面学 过的有理数的加减乘除混合运算法则，我们 应该“先乘除，后加减”来计算这个子．那 么乘方的运算顺序我们又是怎么规定的呢？ 有理数的混合运算应注意的运算顺序： 　　（1）先乘方,再乘除，最后加减； 　　（2）同级运算，从左到右进行； 　　（3）如有括号，先做括号内的运算，按 小括号、中括号、大括号依次进行． 例1：计算：           232432 223           . . . 8 3 16 2 9 2 8 3 18 4 5 8 54 4 5 57 5                       解：原式 例2：观察下面三行数： －3，9，－27，81，－243，729，…；① 0，12，－24，84，－240，733，…；② 10，－17，55，－181，487，－1557，…；③ （1）第①行数按什么规律排列？ （2）第② ③行数与第①行数分别有什 么关系？ （3）取每行数的第9个数， 计算这三个数的和． 解：（1）第①行数是－3，（－3）2 ,（－3）3, （－3）4，···. （2）对比①②两行中位置对应的数，将会发现第②行 数是第①行相应的数加3，即 －3＋3，（－3）2＋3 ,（－3）3＋3,（－3）4＋ 3，···. 对比①③两行中位置对应的数，将会发现第③行数是 第①行对应的数的2倍再加1，即 －3×2＋1，（－3）2×2＋1 , （－3）3×2＋1,（－3）4×2＋1，···. （3）每行数中的第20个数的和是： （－3）9＋[（－3）9＋3] ＋ [（－3）9×2＋1] ＝－19 683＋（－19683＋3） ＋（－19683） ×2＋1 ＝－19 683－19 680－39 366＋1 ＝－78 728. 　　1．把下列各式写成乘方运算的形式，并 指出底数，指数各是多少？          ( ) .5 .5 .5 .5 .5 , ( ) , 3 3 3 3 ( ) (1000). 1 2 2 2 2 2 1 1 1 12 3                                         a a a   1000( ) .5 ( ) ( ) . 3 4 5 11 2 2 3      ； ； a （2）底数分别为： （3）指数分别为：5，4，1000. 1 . 2 - 2.5，- ，a 　　2．如果一个数的偶次幂是正数，那么这 个数是（ ） 　　A．正数 　　　B．负数 　 C．有理数 　　D．非0数 　　3．如果有理数a满足a2