2014年秋七年级（人教版）数学教案：1_2_4绝对值 2页

1 1.2.4 绝对值 教学目标： 1、理解绝对值的概念及其几何意义，通过从数形两个方面理解绝对值的意义， 初步了解数形结合的思想方法。 2、会求一个数的绝对值，知道一个数的绝对值，会求这个数。 3、掌握绝对值的有关性质。 4、通过应用绝对值解决实际问题，培养学生深厚的学习兴趣，提高学生学数学 的好奇心和求知欲。 重点：绝对值的概念 重点：绝对值的几何意义 教学过程： 一、创设情境，引入新课 问题 1：两辆汽车从同一处 O 出发，分别向东、西方向行驶 10km,到达 A、B 两 处。它们行驶的路线相同吗？它们行驶路程的远近相同吗？ 首先，先画出一条数轴表示公路，如果以 O 处为原点，正东方向为正方向，那 么正西则为负方向。再以 10km 为一单位长度，则可用数轴来表示出上题。 问：两辆汽车相距 O 处，即原点 O 的距离是多少？两辆汽车的行驶路线一样吗？ 学生会答：10km，不一样，一辆向东，一辆向西。 通过这个例子我们可以发现，一个地方的位置要用两个因素来确定——方向和距 离。方向通常我们用正、负表示，那么距离呢？它该怎么表示？今天，我们就来 学习新的内容——绝对值。 二、讲授新课 问题 1：请说出在数轴上，+3 和－3 分别在原点的哪边？距离原点有几个单位长 度？那对于－5,+7,0 呢? 请两位同学起来回答。 教师归纳：一般地，数轴上表示数 a 的点与原点的距离叫做数 a 的绝对值。为了 方便，我们用一种符号来表示一个数的绝对值，约定在一个数的两旁各画一条竖 线来表示这个数的绝对值，记作｜a｜，读作 a 的绝对值。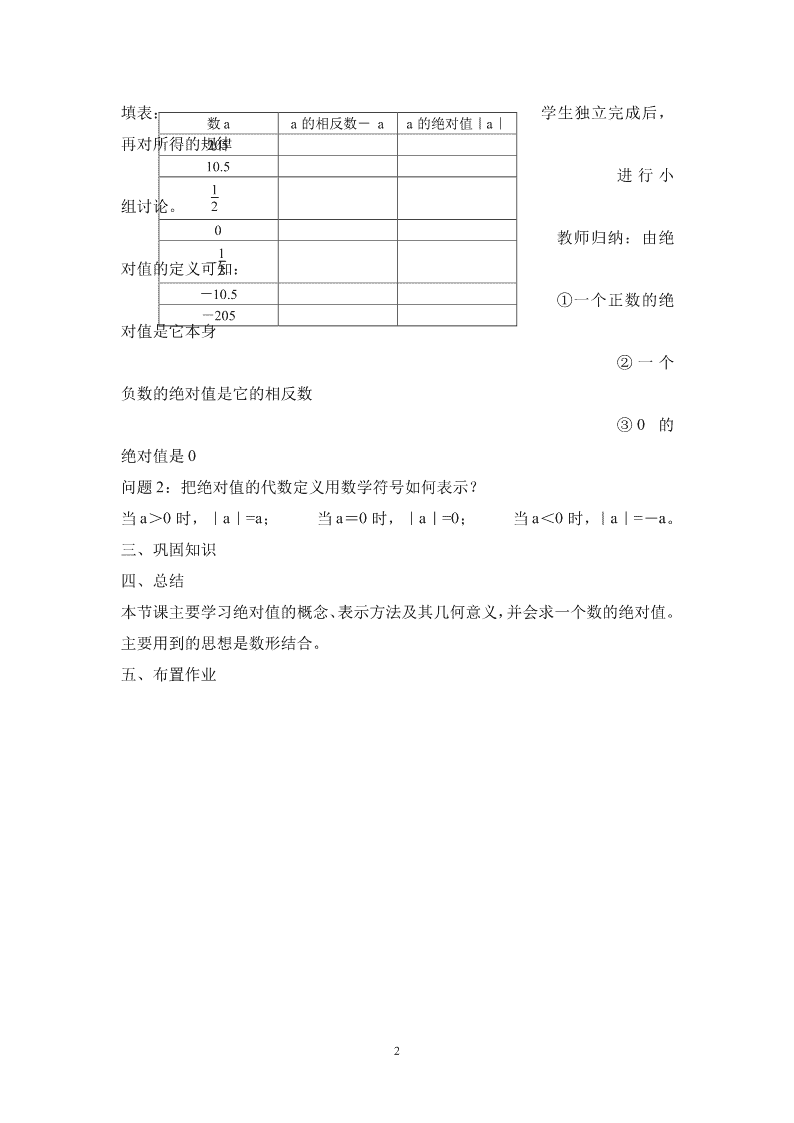 2 填表： 学生独立完成后， 再对所得的规律 进行小 组讨论。 教师归纳：由绝 对值的定义可知： ①一个正数的绝 对值是它本身 ②一个 负数的绝对值是它的相反数 ③ 0 的 绝对值是 0 问题 2：把绝对值的代数定义用数学符号如何表示？ 当 a＞0 时，｜a｜=a； 当 a＝0 时，｜a｜=0； 当 a＜0 时，｜a｜=－a。 三、巩固知识 四、总结 本节课主要学习绝对值的概念、表示方法及其几何意义，并会求一个数的绝对值。 主要用到的思想是数形结合。 五、布置作业 数 a a 的相反数－ a a 的绝对值｜a｜ 205 10.5 1 2 0 －1 2 －10.5 －205