七年级下册数学第四章 三角形 周周测4（4-3） 北师大版 5页

第四章 三角形 周周测4‎ ‎1. 如图,已知∠A=∠D,∠1=∠2,那么要得到△ABC≌△DEF,还应给出的条件可以是(　　)‎ ‎[来源:Zxxk.Com]‎ A. ∠E=∠B B. ED=BC C. AB=EF D. AF=CD ‎2. 下列条件中,能判定△ABC≌△DEF的是(　　)‎ A. AB=DE,BC=EF,∠A=∠E B. ∠A=∠E,AB=EF,∠B=∠D C. ∠A=∠D,∠B=∠E,∠C=∠F D. ∠A=∠D,∠B=∠E,AC=DF ‎3. 如图,AB∥CD,且AB=CD,则△ABE≌△CDE的根据是(　　)‎ ‎[来源:学科网ZXXK]‎ A. 只能用ASA B. 只能用SSS C. 只能用AAS D. 用ASA或AAS[来源:学&科&网Z&X&X&K]‎ ‎4. 如图,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有(　　)‎ A. 1个 B. 2个 C. 3个 D. 4个 ‎5. 如图，(1)连结AD后，当AD＝ ，AB＝ ，BD＝ 时，可用“SSS”推得△ABD≌△DCA.‎ ‎(2)连结BC后，当AB＝ ，BC＝ ，AC＝ 时，可推得△ABC≌△DCB.‎ ‎[来源:学§科§网]‎ ‎6. 如图，在△ABC中，已知AB＝AC，D为BC的中点，则△ABD≌△ACD，根据是 ，AD与BC的位置关系是 .‎ ‎7. 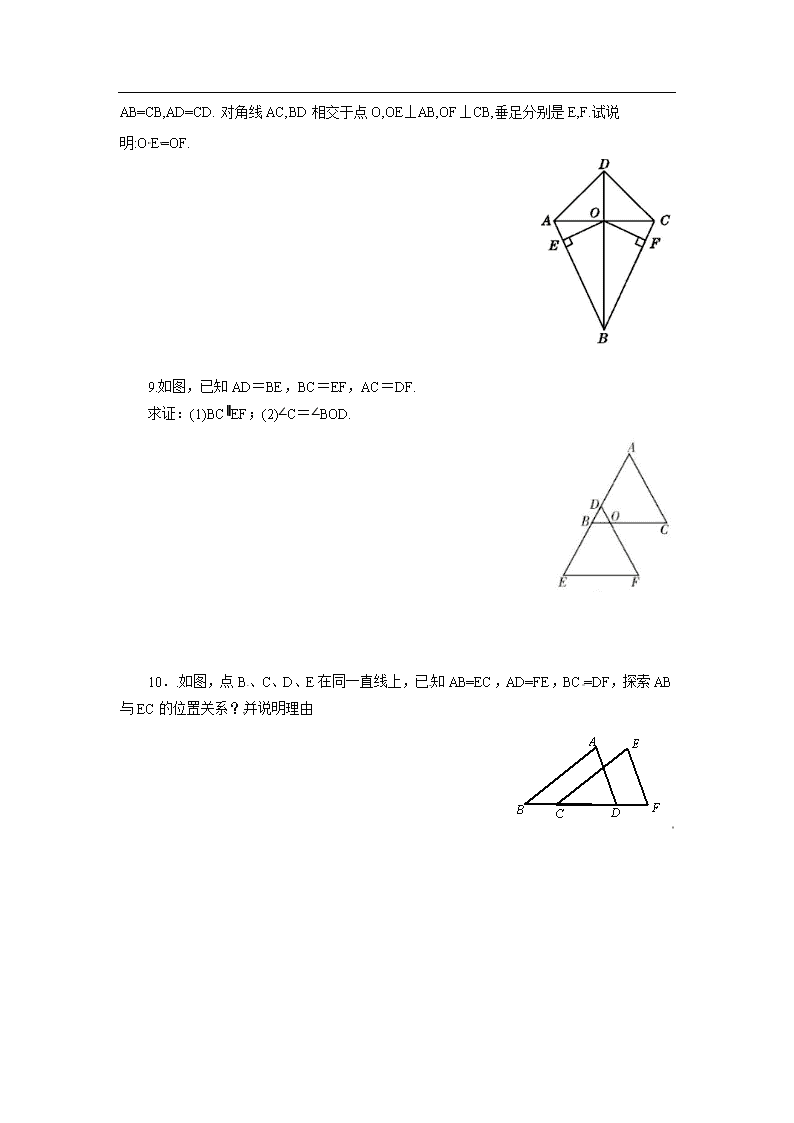如图,在四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90°,且BC=CE.试说明:△ABC与△DEC全等.‎ ‎8.我们把两组邻边相等的四边 形叫做“筝形”.如图,四边形ABCD是一个筝形,其中AB=CB,AD=CD.对角线AC,BD相交于点O,OE⊥AB,OF⊥CB,垂足分别是E,F.试说明:OE=OF.‎ ‎9.如图，已知AD＝BE，BC＝EF，AC＝DF.[来源:学&科&网Z&X&X&K]‎ 求证：(1)BC∥EF；(2)∠C＝∠BOD.[来源:学科网]‎ ‎10．.如图，点B、C、D、E在同一直线上，已知AB=EC，AD=FE，BC=DF，探索AB与EC的位置关系？并说明理由[来源:Z.xx.k.Com]‎ 第四章 三角形 周周测4参考答案与解析 ‎1.D ‎ ‎2. D ‎3. D ‎ ‎4. C ‎5. (1)DA DC CA (2) DC CB DB ‎ ‎6. SSS AD⊥BC ‎7. 解析：∵∠BAE=∠BCE=∠ACD=90°，‎ ‎∴∠DCE+∠ECA=∠ECA+∠ACB，‎ ‎∴∠DCE=∠ACB，且∠B+∠CEA=180°，‎ 又∠DEC+∠CEA=180°，‎ ‎∴∠B=∠DEC，‎ 在△ABC和△DEC中 ,‎ ‎∴△ABC≌△DEC（ASA）．‎ ‎8.解：证明：∵在△ABD和△CBD中，‎ AB=CB，AD=BD，BD=BD，‎ ‎∴△ABD≌△CBD（SSS），[来源:学§科§网Z§X§X§K]‎ ‎∴∠ABD=∠CBD，[来源:Z*xx*k.Com]‎ ‎∴BD平分∠ABC．[来源:学科网]‎ 又∵OE⊥AB，OF⊥CB，‎ ‎∴OE=OF．‎ ‎9. (1)∵AD=BE,[来源:Z+xx+k.Com][来源:学科网ZXXK]‎ ‎∴AD+DB=BE+DB，即AB=DE,‎ ‎∵AB=DE，AC=DF，BC=EF,[来源:Z,xx,k.Com]‎ ‎∴△ABC≌△DEF,‎ ‎∴∠B=∠E,‎ ‎∴BC∥EF ‎(2) ∵BC∥EF,‎ ‎∴∠DOB=∠F,‎ ‎∵∠C=∠F,‎ ‎∴∠DOB=∠C ‎10. AB与EC的位置关系是：AB∥EC.‎ 理由：∵BC=DF，‎ ‎∴BD=CF.‎ 在△ABD和△FCE中 ‎∴△ABD≌△FCE（S.S.S.）‎ ‎∴∠B=∠FCE,∴AB∥EC.‎