七年级下数学课件《同底数幂的乘法》课件4_冀教版 15页

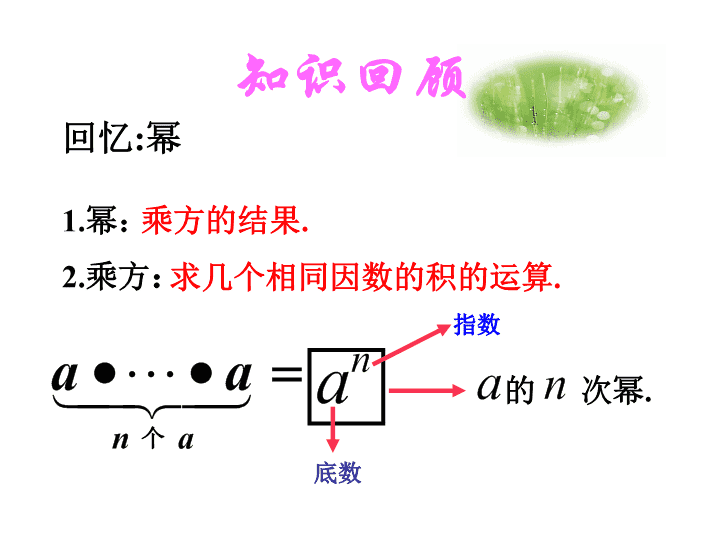
1.幂： 知识回顾 乘方的结果. 个 a n a a a   na 回忆:幂 底数 指数 的 次幂.n 求几个相同因数的积的运算.2.乘方： 2 10 10 3 10 10 10  210 310 个 个 讲授新课 1.同底数幂:就是指底数相同的幂. 2. 两个同底数幂相乘： 指数不同， 底数相同 同底数幂的概念 观察它们的 指数和底数 2 10 10 2 310 10 ?  讲授新课 两个同底数幂相乘： （乘方的意义） （乘法结合律） （乘方的意义） 探索：同底数幂的乘法法则 解： (10 10) (10 10 10)  10 10 10 10 10     510 . 2 310 10 ?  2 310 10 2 3 5 2 310 10 10 10    继续探索： 将上题中的底数10改为任意底数 ，则有 ( )a a a ( )a a a a a a a     5.a a 即， 2 3a a  2 3 5 2 3.a a a a    个 个 m na a  ( ) m a a a   ( ) n a a a  ( ) ( ) m n a a a     m na  .m n m na a a   个 即， 如果我把上题中的指数 3，2改成一般的 任意正整数并分别用字母 来表示.,m n 同底数幂的乘法法则： m n m na a a   （ 都是正整数）, m n 即，同底数幂相乘，底数_____， 指数______. 不变 相加 （1）等号左边是什么运算？ m n m na a a   , m n 法则剖析： （ 都是正整数） （2）等号左右两边的指数有什么关系？ 答：等号左边是乘法运算 . 答： 等号右边的指数是等号左边的两 个指数相加的和. 公式推广： 当三个或三个以上的同底数幂相乘时， 法则可以推广为： m n p m n pa a a a     （ 都是正整数）, ,m n p 即，当幂与幂之间相乘时，只要是底数相 同，就可以直接利用同底数幂的乘法法则： 底数不变，指数相加. 例1 把下列各式表示成幂的形式： 6 3 2 4(1)2 2 ; (2) ; a a  例题讲解 6 32  92 6a 2 4a  ( 1)m mx   2 1mx  解：原式= 解：原式= 解：原式= 1 2 3(3) ; (4) .m mx x a a a   6a 1 2 3a  解：原式= 例2 太阳系的形状像一个以太阳为中心的大圆盘， 光通过这个圆盘半径的时间约为2×104s.光的速 度约为3×105km/s．求太阳系的直径． 解：2×3×105×2×104 ==12×109(km). 答：太阳系的直径约为12×l09km. 1.判断正误： 3 2 6 3 3 4 4 4 5 5 10 (1) ( ) (2) ( ) (3) 2 ( ) (4) ( ) a a a a a a b b b x x x         3 2 5(1)a a a  3 4(2)a a a  4 4 8(3)b b b  5 5 5(4) 2x x x  × × × × 随堂练习 点评：区分是乘法还是加法运算，再选择不同的法 则. 2.填空： 3 1ny  5 -1n 若 则 6 2 1 6 ( ) 12 1 ( ) 2 (1) ______; (2) ; (3) ; (4) 10 100 1000 10 , ____. n n n n x y y a a a a a a a x              点拨：同底数幂乘法公式的逆用也很重要. 3.计算： 2, 3,m na a  ?m na   m na   已知： 求 解： m na a 2 3  6. 注意事项： 1.同底数幂相乘，底数不变，指数相加.对这个法 则要注重理解“同底，相乘，不变，相加”这八 个字. 2.底数可以是一个数，也可以是单项式或多项式. 运算时不同底的要先化为同底的，才可以运用法 则. 4.解题时，要注意指数为1的情况，不要漏掉. 3.解题时，底数是负数的要用括号把底数括起来.