人教版七年级上数学教学课件：从算式到方程（2） 34页

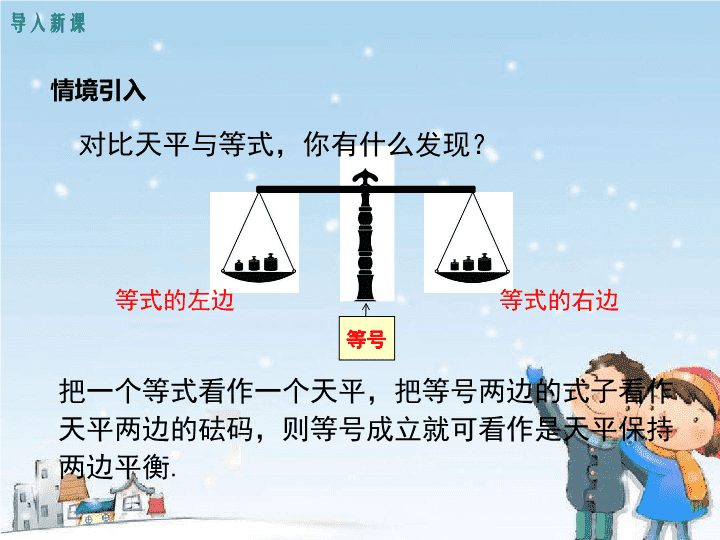
第三章 一元一次方程 导入新课 讲授新课 当堂练习 课堂小结 3.1 从算式到方程 3.1.2 等式的性质 学习目标 1. 理解、掌握 等式的性质 . ( 重点 ) 2. 能正确应用等式的性质解简单的一元一次方程 . ( 难点 ) 对比天平与等式，你有什么发现？ 把一个等式看作一个天平，把等号两边的式子看作天平两边的砝码，则等号成立就可看作是天平保持两边平衡 . 等号 等式的左边 等式的右边 导入新课 情境引入 √ √ √ √ √ 下列各式中哪些是等式？ ； ； ； ④ 3 ； ； ⑥2+3=5 ； ⑦3×4=12 ； ⑧9 x +10=19 ； ； . 用 等号 表示 相等关系 的式子叫做 等式 . 我们可以用 a = b 表示一般的等式 . 讲授新课 等式的性质 一 观察与思考 观察天平有什么特性？ 天平两边同时加入相同质量的砝码 天平仍然平衡 天平两边同时拿去相同质量的砝码 天平仍然平衡 天平 两边同时 天平仍然平衡 加入 拿去 相同质量的砝码 相同的 数 ( 或式子 ) 等式 两边同时 加上 减去 等式 仍然成立 换言之， 等式两边加 ( 或减 ) 同一个数 ( 或式子 ) ，结果仍相等 . 如果 a = b ，那么 a ± c = b ± c . 合作探究 等式的性质 1 由天平看等式的性质 2 你能发现什么规律？ 等式两边乘同一个数，或除以同一个不为 0 的数，结 果仍相等 . 等式的性质 2 如果 a = b ，那么 ac = bc ； 如果 a = b （ c ≠0 ），那么 . ( 2 ) 怎样从等式 3+ x= 1 得到等式 x = － 2? ( 3 ) 怎样从等式 4 x= 12 得到等式 x = 3? 依据等式的性质 1 两边同时减 3. 依据等式的性质 2 两边同时除以 4 或同乘 . 依据等式的性质 2 两边同时除以 或同乘 100. 例 1 ( 1 ) 怎样 从 等式 x － 5 = y － 5 得到 等式 x = y ? 依据等式的性质 1 两边同时加 5. 典例精析 ( 4 ) 怎样从等式 得到等式 a = b ? 例 2 已知 mx = my ，下列结论错误的是 （ ） A. x = y B. a + mx = a + my C. mx － y = my － y D. amx = amy 解析：根据等式的性质 1 ，可知 B 、 C 正确；根据等式的性质 2 ，可知 D 正确；根据等式的性质 2 ， A 选项只有 m ≠0 时才成立，故 A 错误，故选 A ． A 易错提醒： 此类判断等式变形是否正确的题型中，尤其注意利用等式的性质 2 等式两边同除某个字母参数，只有这个字母参数确定不为 0 时，等式才成立 . ( 2 ) 从 a+ 2 =b+ 2 能不能得到 a=b ，为什么 ? ( 3 ) 从 － 3 a= － 3 b 能不能得到 a=b ，为什么 ? ( 4 ) 从 3 ac= 4 a 能不能得到 3 c= 4 ，为什么 ? 说一说 ( 1 ) 从 x = y 能不能得到 ，为什么 ? 能，根据等式的性质 2 ，两边同时除以 9 能，根据等式的性质 1 ，两边同时加上 2 能，根据等式的性质 2 ，两边同时除以 -3 不能， a 可能为 0 利用等式的性质解方程 二 例 3 利用等式的性质解下列方程： ( 1 ) x + 7 = 26 解 : 得 方程两边同时减去 7 ， x + 7 = 26 － 7 － 7 于是 = x 19 小结： 解一元一次方程要 “ 化归 ” 为 “ x=a ” 的形式 . 两边同时除以－ 5 ， 得 解 : 方程 ( 2 ) － 5 x = 20 思考： 为使 ( 2 ) 中未知项的系数化为 1 ，将要用到等式的什么性质 ？ 化简，得 x = － 4 - 5 x ÷( － 5)= 20 ÷( － 5) 解：方程两边同时加上 5 ，得 化简，得 方程两边同时 乘 － 3 ， 得 x = － 27 x = － 27 是原方程的解吗 ? 思考 ：对比 ( 1 ) ， ( 3 ) 有什么新特点 ？ ( 3 ) 一般地，从方程解出未知数的值以后，可以代入原方程检验，看这个值能否使方程的两边相等 . 例如， 将 x = － 27 代入方程 的左边， 方程的左右两边相等，所以 x = － 27 是原方程的解 . 针对训练： ( 1 ) x +6 = 17 ; ( 2 ) - 3 x = 15 ; ( 4 ) ( 3 ) 2 x - 1 = - 3 ; 解： (1) 两边同时减去 6 ，得 x =11. (2) 两边同时除以 -3 ，得 x =-5. (3) 两边同时加上 1 ，得 2 x = - 2. 两边同时除以 2 ，得 x = - 1. (4) 两边同时加上 - 1 ，得 两边同时乘以 - 3 ，得 x = 9 . 当堂练习 A 2. 下列各式变形正确的是 （ ） A. 由 3 x － 1= 2 x +1 得 3 x － 2 x =1+1 B. 由 5+1= 6 得 5= 6+1 C. 由 2( x +1) = 2 y +1 得 x +1= y +1 D. 由 2 a + 3 b = c － 6 得 2 a = c － 18 b 1. 下列说法正确的是 _______ A. 等式都是方程 B. 方程都是等式 C. 不是方程的就不是等式 D. 未知数的值就是方程的解 B 3. 下列变形，正确的是 （ ） A. 若 ac = bc ，则 a = b B. 若 ，则 a = b C. 若 a 2 = b 2 ，则 a = b D. 若 ，则 x = － 2 B 4 . 填空 ( 1 ) 将等式 x － 3=5 的两边都 _____ 得到 x =8 ，这是 根据等式的性质 __ ； ( 2 ) 将等式 的两边都乘以 ___ 或除以 ___ 得 到 x = － 2 ，这是根据等式性质 ___ ； 加 3 1 2 2 减 y 1 除以 x 2 ( 3 ) 将等式 x + y =0 的两边都 _____ 得到 x = － y ，这是 根据等式的性质 ___ ； ( 4 ) 将等式 xy =1 的两边都 ______ 得到 ，这是根据等 式的性质 ___ ． 　 5. 应用等式的性质解下列方程并检验 : ( 1 ) x+ 3= 6 ； ( 2 ) 0.2 x =4 ； ( 3 ) -2 x +4=0 ； ( 4 ) 解： (1) x =3 ； (2) x =20 ； (4) x = － 4. 6. 已知关于 x 的方程 和方程 3 x － 10 =5 的解相同，求 m 的值 . 解：方程 3 x － 10 =5 的解为 x =5 ，将其代入方程 ，得到 ，解得 m =2. 课堂小结 等式的 性质 性质 1 性质 2 应用 如果 a = b ，那么 a ± c = b ± c . 如果 a = b ，那么 ac = bc ； 如果 a = b （ c ≠0 ），那么 . 运用等式的性质把方程 “化归” 为最简的形式 x = a