七年级下册数学教案5-2-2 第1课时 平行线的判定 人教版 5页

第五章 相交线与平行线 ‎5.2 平行线及其判定 ‎5教学备注 ‎【自学指导提示】‎ 学生在课前完成自主学习部分 .2.2 平行线的判定 第1课时 平行线的判定[来源:学#科#网]‎ 学习目标：1.掌握平行线的三种判定方法，能运用平行线的判定方法解决问题.‎ ‎2.通过独立思考，小组探究，理解角与线的位置关系之间的联系，体会数形结合思想.‎ ‎3.激情投入，善于发现问题和提出问题，感受学习数学的乐趣.‎ 重点：三种判定方法判定两直线平行.‎ 难点：根据平行线的判定方法进行简单的推理.‎ 自主学习 一、知识链接 ‎1.在同一平面内， 的两条直线叫做平行线. ‎ ‎2.过已知直线外一点能且只能画 条直线与这条直线垂直，能且只能画 条直线与这条直线平行.‎ ‎3.同位角、内错角、同旁内角的定义是怎样叙述的？‎ ‎4.怎样用三角板和直尺作已知直线的平行线？‎ 二、新知预习 ‎1.试利用三角板和直尺，经过直线外一点P画出已知直线AB的平行线CD，由此你会发现什么？‎ ‎2.同位角 ，两直线平行.‎ 三、自学自测 ‎1.如图,三角形ABC中，∠A=70°，∠BED=70°，可以判断 ∥ .根据是 .由∠B=48°，∠FDC=48°，可以判断 ∥ .根据是 .‎ ‎ 第1题图 第2题图 ‎ ‎2.如图，用直尺和三角板作直线AB，CD，从图中可知，直线AB与直线CD的位置关系为 .‎ 四、我的疑惑 ‎______________________________________________________________________________________________________________________________________________________‎ 教学备注 配套PPT讲授 ‎1.情景引入 ‎（见幻灯片3）‎ ‎2.探究点1新知讲授 ‎（见幻灯片5-13）‎ ‎3.探究点2新知讲授 ‎（见幻灯片14-23）‎ 课堂探究 一、 要点探究 探究点1：利用同位角判定两条直线平行 画一画：用三角尺和直尺画平行线的步骤有哪些？ ‎ ‎ ‎ 思考：（1）画图过程中，什么角始终保持相等？‎ （2） 直线a，b位置关系如何？ ‎ ‎（3）由上面的操作过程，你能发现判定两直线平行的方法吗？‎ 总结归纳：‎ 判定方法1：两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.‎ 简单说成：同位角相等，两直线平行.‎ 应用格式： ∵∠1=∠2(已知)，∴a∥b（同位角相等，两直线平行）‎ 做一做：下图中若∠1=55°，∠2=55°，直线AB、CD平行吗？为什么?‎ 探究点2：利用内错角、同旁内角判定两条直线平行 问题1：如图，由∠3=∠2，可推出a//b吗？如何推出？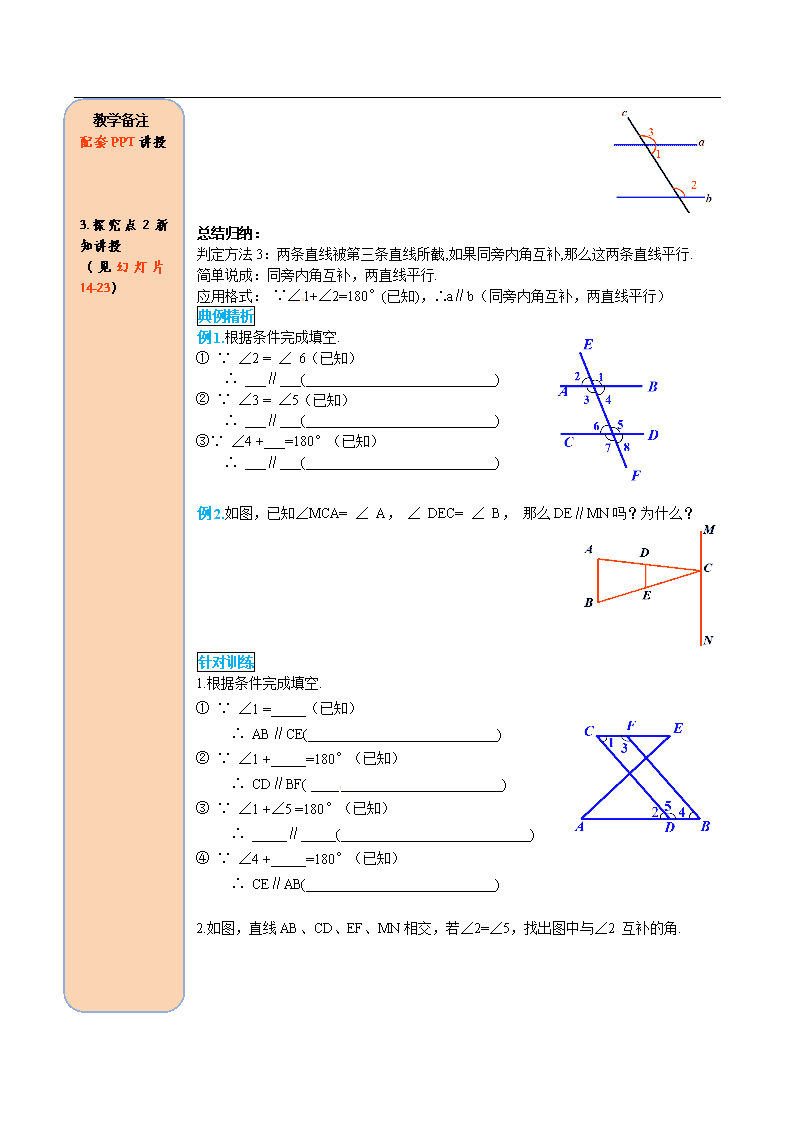‎ 总结归纳：‎ 判定方法2：两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.‎ 简单说成：内错角相等，两直线平行.‎ 应用格式： ∵∠3=∠2(已知)，∴a∥b（内错角相等，两直线平行）‎ 问题2：如图，如果∠1+∠2=180°，你能判定a//b吗?‎ 总结归纳：‎ 判定方法3：两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.‎ 简单说成：同旁内角互补，两直线平行.‎ 应用格式： ∵∠1+∠2=180°(已知)，∴a∥b（同旁内角互补，两直线平行）‎ 教学备注 配套PPT讲授 ‎3.探究点2新知讲授 ‎（见幻灯片14-23）‎ 典例精析 例1.根据条件完成填空.‎ ‎① ∵ ∠2 = ∠ 6（已知）‎ ‎ ∴ ___∥___(___________________________)‎ ‎② ∵ ∠3 = ∠5（已知）‎ ‎ ∴ ___∥___(___________________________)‎ ‎③∵ ∠4 +___=180°（已知）‎ ‎ ∴ ___∥___(___________________________)‎ 例2.如图，已知∠MCA= ∠ A， ∠ DEC= ∠ B， 那么DE∥MN吗？为什么？‎ 针对训练 ‎1.根据条件完成填空. ‎ ‎① ∵ ∠1 =_____（已知）‎ ‎ ∴ AB∥CE(___________________________)‎ ‎② ∵ ∠1 +_____=180°（已知）‎ ‎ ∴ CD∥BF( ___________________________)‎ ‎③ ∵ ∠1 +∠5 =180°（已知）‎ ‎ ∴ _____∥_____(___________________________)‎ ‎④ ∵ ∠4 +_____=180°（已知）‎ ‎ ∴ CE∥AB(___________________________)[来源:Z*xx*k.Com]‎ ‎2.如图，直线AB、CD、EF、MN相交，若∠2=∠5，找出图中与∠2 互补的角.‎ 二、课堂小结 文字叙述 符号语言 图形 ‎ 相等，‎ 两直线平行 ‎∵ (已知),‎ ‎∴a∥b ‎ 相等，‎ 两直线平行 ‎∵ (已知),‎ ‎∴a∥b[来源:学*科*网Z*X*X*K]‎ ‎ 互补，‎ 两直线平行 ‎∵ (已知)‎ ‎∴a∥b[来源:Z+xx+k.Com]‎ 教学备注 配套PPT讲授 ‎4.课堂小结 ‎5.当堂检测 ‎（见幻灯片24-28）‎ 当堂检测 ‎1.如图,可以确定AB∥CE的条件是( )[来源:学|科|网Z|X|X|K]‎ A.∠2=∠B B. ∠1=∠A C. ∠3=∠B D. ∠3=∠A 第1题图 第2题图 ‎ ‎2.如图,已知∠1=30°,∠2或∠3满足条件 ，则a//b.‎ ‎3.如图.（1）从∠1=∠4，可以推出 ∥ ，理由是 .‎ ‎ (2)从∠ABC +∠ =180°，可以推出AB∥CD ，理由是 .‎ ‎(3)从∠ =∠ ，可以推出AD∥BC，‎ 理由是 .‎ ‎(4)从∠5=∠ ，可以推出AB∥CD，理由是 .‎ ‎4.如图，已知∠1= ∠3，AC平分∠DAB，你能判断哪两条直线平行？请说明理由？‎