初中数学7年级教案：第7讲 平行线的性质 9页

辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目： ‎ 授课日期 ‎××年××月××日 ‎ 时 间 A / B / C / D / E / F段 主 题 平行线的性质 教学内容 1． 掌握平行线的性质，通过平行线性质的运用，体会文字语言、图形语言、符号语言之间的转换和一致，逐步提高分析能力与简单的逻辑推理能力．‎ 2． 理解两条通过平行线间的距离，体会两点的距离、点到直线的距离、两条平行线间的距离概念之间的联系．‎ ‎（以提问的形式回顾）‎ ‎1. 平行线的性质是什么？‎ u 性质1：两直线平行，同位角相等 u 性质2：两直线平行，内错角相等 u 性质3：两直线平行，同旁内角互补 ‎2. 平行线间的距离有什么特征？‎ 两条平行线中，任意一条直线上的所有点到另一条直线的距离都是一个定值 小练习：‎ ‎1．如图，分别交于 平分 ‎，则的度数是___________． ‎ ‎2．如图，，直线分别交、于点、，平分，‎ ‎，则的度数是____________． ‎ A M E B D G N F C ‎1‎ ‎ ‎A E ‎1‎ C G F D B ‎2‎ ‎3．如图，把矩形沿对折，若，则等于____________．‎ ‎4．如图，已知平分，，如果，，‎ 那么 ．‎ A B C D E F ‎1‎ 参考答案：1、65°； 2、100°； 3、115°； 4、62°‎ ‎（采用教师引导，学生轮流回答的形式）‎ 例1. 如图，已知ΔABC中，CD⊥AB，EF⊥AB，∠1=∠2，∠B=50°，求∠ADG的度数。‎ ‎ 解：∵CD⊥AB，EF⊥AB（ ）‎ ‎ ∴CD∥EF（ ）‎ ‎ ∴∠2=∠3（ ）‎ ‎ ∵∠1=∠2（已知） ‎ ‎ ∴∠1=∠3（ ）‎ ‎∴DG∥BC（ ）‎ ‎∴∠ADG=∠B（ ）‎ ‎∵∠B=50°（已知）‎ ‎∴∠ADG=50°（ ）‎ 参考答案：已知；垂直于同一直线的两直线平行；两直线平行，同位角相等；等量代换；内错角相等，两直线平行；两直线平行，同位角相等；等量代换。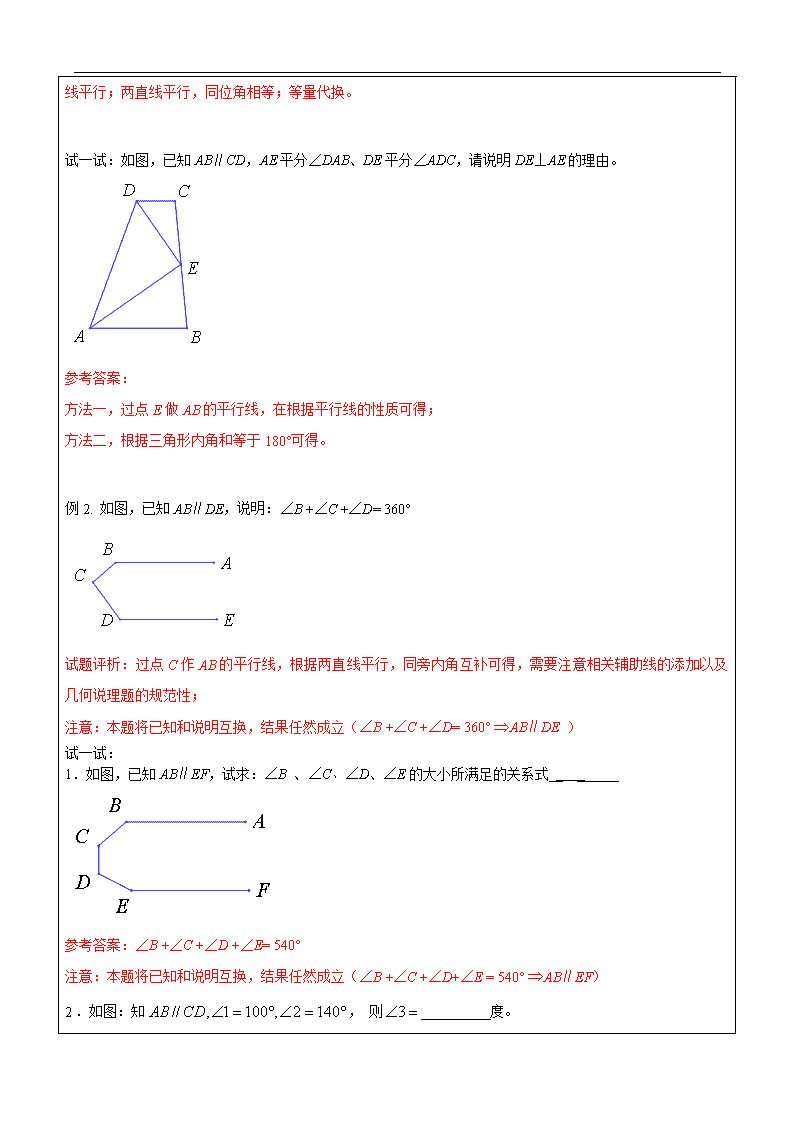‎ 试一试：如图，已知AB∥CD，AE平分∠DAB、DE平分∠ADC，请说明DE⊥AE的理由。‎ 参考答案：‎ 方法一，过点E做AB的平行线，在根据平行线的性质可得；‎ 方法二，根据三角形内角和等于180°可得。‎ 例2. 如图，已知AB∥DE，说明：∠B +∠C +∠D= 360°‎ 试题评析：过点C作AB的平行线，根据两直线平行，同旁内角互补可得，需要注意相关辅助线的添加以及几何说理题的规范性；‎ 注意：本题将已知和说明互换，结果任然成立（∠B +∠C +∠D= 360°AB∥DE ）‎ 试一试：‎ ‎1．如图，已知AB∥EF，试求：∠B 、∠C、∠D、∠E的大小所满足的关系式__ ______‎ 参考答案：∠B +∠C +∠D +∠E= 540°‎ 注意：本题将已知和说明互换，结果任然成立（∠B +∠C +∠D+∠E = 540°AB∥EF）‎ ‎2．如图：知， 则__________度。 ‎ 参考答案：60°。‎ 例3. 如图，已知AB∥DE，说明：∠B +∠D =∠C 试题评析：过点C作AB的平行线，根据两直线平行，内错角相等可得，需要注意相关辅助线的添加以及几何说理题的规范性；‎ 试一试：‎ ‎1． 如图，AEFC是折线，直线AB∥CD，试写出∠A、∠E、∠F、∠C的大小所满足的关系式____________________‎ ‎ ‎ 参考答案：∠E+∠F-∠A-∠C=180°；‎ 评析：过点E、F作AB的平行线可得。‎ ‎2． 如图，已知：AB∥CD，试猜想、、三个角之间的数量关系，并说明理由。‎ ‎ ‎ 参考答案：∠P=∠C-∠A； ∠P=∠A-∠C；‎ 评析：过点P作AB的平行线可得。‎ ‎3．如图，CD∥EF，∠EFB=70°，∠FBC=80°，求∠BCD的度数。‎ 参考答案：∠BCD=30°‎ 评析：方法一：过点B作CD的平行线，根据平角可得。‎ 方法二：延长CD交BF于G点，在根据三角形内角和等于180°可得。‎ 例4. 如图，已知，，三角形的面积为．求三角形的面积．‎ 解：过点A作AE⊥BC，垂足为E，过点C作CF⊥AD，垂足为F 因为∠1=∠2（已知）‎ 所以AD∥BC（内错角相等，两直线平行）‎ 所以AE=CF（平行线间距离的意义）‎ 因为 因为（已知）‎ 所以 试一试：在中，，是的外角的平分线，是上的一点．试说明与的面积相等．‎ 评析：本题的重点是证明AE∥BC，其余解题过程同例题。‎ ‎（学生统一完成，互相批改，教师针对重难点详细讲解）‎ ‎1．一张长方形纸条，按如图所示折叠一下，则＝_________． 65°‎ ‎2．如图，AB∥CD，若∠ABE＝120°，∠C＝35°，则∠BEC＝__________． 95°‎ ‎3．如图AB∥CD，∠NCM＝90°，∠NCB＝30°，CM平分∠BCE，则∠B＝__________．60°‎ ‎4．如图，已知在梯形ABCD中，AD∥BC， AC、BD相交于点O，且，则ΔCOD的面积＝________． 21‎ ‎ ‎ D ‎1‎ A E F B G C ‎2‎ ‎5．已知：如图，DG⊥BC AC⊥BC，EF⊥AB，∠1=∠2．求证：CD⊥AB 证明：∵DG⊥BC，AC⊥BC(___________)‎ ‎ ∴∠DGB=∠ACB=90º(垂直的定义)‎ ‎ ∴DG∥AC（_____________________）‎ ‎ ∴∠2=_____(_____________________)‎ ‎ ∵∠1=∠2(__________________) ‎ ‎∴∠1=∠__________(等量代换) ‎ ‎ ∴EF∥CD(______________________) ‎ ‎∴∠AEF=∠________________(____________________)‎ ‎∵EF⊥AB (________________) ‎ ‎∴∠AEF=90º (_________________________)‎ ‎∴∠ADC=90º (___________________)‎ ‎∴CD⊥AB(__________________________)‎ ‎5、略 ‎6．如图：已知∠B=∠D，AD∥BC，请说明∠E=∠F的理由。‎ 解：因为AD∥BC（已知）‎ 所以∠D=∠BCF（两直线平行线，同位角相等）‎ 因为∠B=∠D（已知）‎ 所以∠B=∠BCF（等量代换）‎ 所以AB∥CD （同位角相等，两直线平行）‎ 所以∠E=∠F（两直线平行，内错角相等）‎ ‎7．已知：如图∠1=∠2，∠C=∠D，试说明∠A=∠F相等 解：因为∠1=∠DGF，∠2=∠ACH（对顶角相等）‎ 因为∠1=∠2（已知）‎ 所以∠DGF=∠ACH（等量代换）‎ 所以DB∥EC（内错角相等，两直线平行）‎ 所以∠C=∠ABD（两直线平行，同位角相等）‎ 因为∠C=∠D（已知）‎ 所以∠D=∠ABD（等量代换）‎ 所以DF∥AC（内错角相等，两直线平行）‎ 所以∠A=∠F（两直线平行，内错角相等）‎ ‎8．如图，已知：AD⊥BC，EF⊥BC，∠E＝∠AGE。说明：AD平分∠BAC。‎ 解：因为AD⊥BC，EF⊥BC（已知）‎ 因为AD∥EF（垂直于同一直线的两直线平行）‎ 所以∠E=∠CAD（两直线平行，同位角相等）‎ ‎∠AGE=∠BAD（两直线平行，内错角相等）‎ 因为∠E＝∠AGE（已知）‎ 所以AD平分∠BAC（角平分线的意义）‎ ‎ ‎ 本节课主要知识点：平行线的性质及应用 ‎ ‎【巩固练习】‎ ‎1．如图，已知，∠ADE=∠B．∠1+∠2=180°请填写∠FGB=∠CDB的理由.‎ 解：因为 ∠ADE=∠B （已知），‎ ‎ 所以_____∥______（ 　　 ）． ‎ ‎ 得∠1 =∠3 （ 　　　 　 ）．‎ ‎ 由∠1+∠2 = 180°（ 已 知 ），　‎ 得∠3+∠2 = 180°（ 　　　 　 ）．‎ 所以_____∥______( 　　　　　 ) ．‎ 所以∠FGB=∠CDB（ ）．‎ 答案：DE∥BC （同位角相等，两直线平行）；两直线平行，内错角相等；等量代换；DC∥GF（同旁内角互补，两直线平行）；两直线平行，同位角相等。‎ ‎2．如图，已知直线AB、CD被直线EF所截，GE平分∠AEF，GF平分∠EFC，∠1+∠2=90°，AB//CD吗？为什么？‎ 解：因为GE平分∠AEF， GF平分∠EFC（已知）‎ 所以∠AEF＝2∠________；∠EFC＝2∠_______。（ ）‎ 所以∠AEF+∠EFC＝_________________（等式性质）‎ 因为∠1+∠2=90°（已知）‎ 所以∠AEF+∠EFC＝____________‎ 所以AB//CD（ ）‎ 答案：∠1，∠2，角平分线的意义；2∠1+2∠2；180°；同旁内角互补，两直线平行。‎ ‎3．如图，已知B、C、D三点在同一条直线上，∠B=∠1, ∠2=∠E，试说明AD//EC.‎ 解：因为∠B=∠1（已知）‎ ‎ 所以AB∥DE（同位角相等，两直线平行）‎ ‎ 得∠2=∠ADE（两直线平行，内错角相等）‎ 因为∠2=∠E（已知）‎ 得∠ADE=∠E（等量代换）‎ ‎ 所以AD∥EC（内错角相等，两直线平行）‎ ‎【预习思考】‎ 1. 如图，那么点A到BC的距离是_____，点B到AC的距离是_______，点A、B两点的距离是_____，点C到AB的距离是________．‎ 2. 设、b、c为平面上三条不同直线，‎ a) 若，则a与c的位置关系是_________；‎ b) 若，则a与c的位置关系是_________；‎ c) 若，，则a与c的位置关系是________．‎