八年级下数学课件：第十八章 平行四边形 复习（共33张PPT）_人教新课标 33页

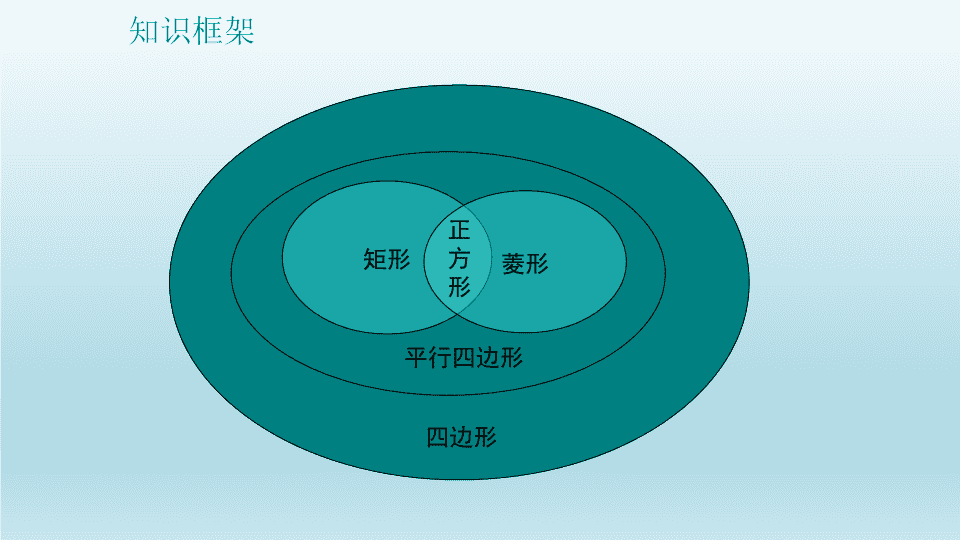
复习课件 第十八章 平行四边形 四边形 知识框架 矩形 菱形 正 方 形 平行四边形 两组对 边平行 一 个 角 是 直 角一组邻边相等 一组邻边相等 一个角是直角 一个角是直角且一组邻边相等 一、几种特殊四边形的性质 项目 四边形 边 角 对角线 对称性 对边平行 且相等 对边平行 且相等 对边平行 且四边相等 对边平行 且四边相等 对角相等 四个角 都是直角 对角相等 四个角 都是直角 互相平分 互相平分且相等 互相垂直平分且相等，每 一条对角线平分一组对角 轴对称图形 轴对称图形 轴对称图形 互相垂直且平分，每一条 对角线平分一组对角 四边形 条件 平行 四边形 矩形 菱形 正方形 二、几种特殊四边形的常用判定方法： 1.定义：两组对边分别平行 2.两组对边分别相等 3.两组对角分别相等 4.对角线互相平分 5.一组对边平行且相等 1.定义：有一个角是直角的平行四边形 2.对角线相等的平行四边形 3.有三个角是直角的四边形 1.定义：一组邻边相等的平行四边形；2.对角线互相 垂直的平行四边形；3.四条边都相等的四边形 1.定义：一组邻边相等且有一个角是直角的平行四边形 2.有一组邻边相等的矩形 3.有一个角是直角的菱形 5种判 定方法 三个角是直角 四条边相等 一 个 角 是 直 角 或 对 角 线 相 等 一组邻边相等 或对角线垂直 一组邻边相等 或对角线垂直 一个角是直角 或对角线相等 一个角是直角且一组邻边相等 三、平行四边形、矩形、菱形、正方形之间的关系 四、其他重要概念及性质 1.两条平行线之间的距离： 2.三角形的中位线定理： 两条平行线中，一条直线上任意一点到另一条直 线的距离叫做两条平行线之间的距离. 三角形的中位线平行于第三边，并且等于第三边的一半. 3.直角三角形斜边上的中线： 直角三角形斜边上的中线等于斜边的一半. 考点一 平行四边形的性质与判定 考点讲练 例1 如图，在直角梯形ABCD中，AD∥BC，∠B＝ 90°，AG∥CD交BC于点G，点E、F分别为AG、CD 的中点，连接DE、FG. (1)求证：四边形DEGF是平行四边形； (2)如果点G是BC的中点，且BC＝12，DC＝10，求 四边形AGCD的面积． 解：(1)∵AG∥DC，AD∥BC， ∴四边形AGCD是平行四边形， ∴AG＝DC. ∵E、F分别为AG、DC的中点， ∴GE＝ AG，DF＝ DC， 即GE＝DF，GE∥DF， ∴四边形DEGF是平行四边形. (2)∵点G是BC的中点，BC＝12， ∴BG＝CG＝ BC＝6. ∵四边形AGCD是平行四边形，DC＝10， AG＝DC＝10， 在Rt△ABG中，根据勾股定理得AB＝8， ∴四边形AGCD的面积为6×8＝48. 1 2 1 2 1 2 例2 在△ABC中，AB=AC，点D在边BC所在的直线上， 过点D作DF∥AC交直线AB于点F，DE∥AB交直线AC 于点E． (1)当点D在边BC上时，如图①，求证：DE+DF=AC． 证明：∵DF∥AC，DE∥AB， ∴四边形AFDE是平行四边形． ∴AF=DE. ∵DF∥AC，∴∠FDB=∠C, 又∵AB=AC， ∴∠B=∠C， ∴∠FDB=∠B， ∴DF=BF， ∴DE+DF=AF+BF=AB=AC. （2）当点D在边BC的延长线上时，如图②；当点D在 边BC的反向延长线上时，如图③，请分别写出图②、 图③中DE，DF，AC之间的数量关系，不需要证明． （3）若AC=6，DE=4，求DF的值． 解：（2）图②中：AC+DE=DF． 图③中：AC+DF=DE． （3）当如图①的情况，DF=AC-DE=6-4=2； 当如图②的情况，DF=AC+DE=6+4=10． 针对训练 2.如图，在▱ ABCD中，对角线AC和BD交于点O， AC=24cm，BD=38cm，AD=28cm，则△BOC的周 长是 （ 　　） A．45cm B．59cm C．62cm D．90cm B 1.如图，在▱ ABCD中，∠ODA=90°，AC=10cm， BD=6cm，则AD的长为 （　　） A．4cm B．5cm C．6cm D．8cm A 3.如图是某公交汽车挡风玻璃的雨刮器，其工作 原理如图．雨刷EF⊥AD，垂足为A，AB=CD且 AD=BC，这样能使雨刷EF在运动时，始终垂直于 玻璃窗下沿BC，请证明这一结论． 证明：∵AB=CD，AD=BC， ∴四边形ABCD是平行四边形， ∴AD∥BC. 又∵EF⊥AD， ∴EF⊥BC． 图 图 考点二 三角形的中位线 例3 如图，在△ABC中，点D，E，F分别是AB，BC， CA的中点，AH是边BC上的高． （1）求证：四边形ADEF是平行四边形； （2）求证：∠DHF=∠DEF． 证明：（1）∵点D，E，F分别是AB，BC，CA的中点， ∴DE、EF都是△ABC的中位线， ∴EF∥AB，DE∥AC， ∴四边形ADEF是平行四边形. （2）∵四边形ADEF是平行四边形， ∴∠DEF=∠BAC， ∵D，F分别是AB，CA的中点， AH是边BC上的高， ∴DH=AD，FH=AF， ∴∠DAH=∠DHA，∠FAH=∠FHA， ∵∠DAH+∠FAH=∠BAC， ∠DHA+∠FHA=∠DHF， ∴∠DHF=∠BAC， ∴∠DHF=∠DEF． 例4 如图，在Rt△ABC中，∠ACB=90°，点D，E 分别是边AB，AC的中点，延长BC到点F，使CF= BC．若AB=12，求EF的长． 解：连接CD， ∵点D，E分别是边AB，AC的中点， ∴DE∥BC，DE= BC，DC= AB. ∵CF= BC， ∴DE ∥FC，DE =FC， ∴四边形DEFC是平行四边形， ∴DC=EF， ∴EF= AB=6． 1 2 1 2 1 21 2 1 2 针对训练 5.如图，是屋架设计图的一部分，点D是斜梁AB的中 点，立柱BC、DE垂直于横梁AC，AB=4m，∠A=30°， 则DE等于 （　　） A．1m B．2m C．3m D．4m A 4.如图，等边三角形ABC中，点D，E分别为AB， AC的中点，则∠DEC的度数为（　　） A．150° B．120° C．60° D．30° B 6.如图，在△ABC中，∠CAB=90°，DE、DF是 △ABC的中位线，连接EF、AD，求证：EF=AD． 证明：∵DE，DF是△ABC的中位线， ∴DE∥AB，DF∥AC， ∴四边形AEDF是平行四边形， 又∵∠BAC=90°， ∴平行四边形AEDF是矩形， ∴EF=AD． 考点三 特殊平行四边形的性质与判定 例5 如图，在矩形ABCD中，对角线AC与BD相交于 点O，过点A作AE∥BD，过点D作ED∥AC，两线相 交于点E． 求证：四边形AODE是菱形； 证明：∵AE∥BD，ED∥AC， ∴四边形AODE是平行四边形. ∵四边形ABCD是矩形， ∴AC=BD，OA=OC= AC， OB=OD= BD， ∴OA=OC=OD， ∴四边形AODE是菱形. 1 21 2 【变式题】如图，O是菱形ABCD对角线的交点，作 BE∥AC，CE∥BD，BE、CE交于点E，四边形CEBO是 矩形吗？说出你的理由. D A B C EO 解：四边形CEBO是矩形. 理由如下：已知四边形ABCD是菱形. ∴AC⊥BD. ∴∠BOC=90°. ∵BE∥AC，CE∥BD， ∴四边形CEBO是平行四边形. ∴四边形CEBO是矩形. 例6 如图，已知在四边形ABFC中，∠ACB＝90°， BC的垂直平分线EF交BC于点D，交AB于点E，且 CF＝AE； (1)试判断四边形BECF是什么四边形？并说明理由； (2)当∠A的大小满足什么条件时，四边形BECF是 正方形？请回答并证明你的结论． 解：(1)四边形BECF是菱形． 理由如下：∵EF垂直平分BC， ∴BF＝FC，BE＝EC， ∴∠3＝∠1. ∵∠ACB＝90°， ∴∠3＋∠4＝90°，∠1＋∠2＝90°，∴∠2＝∠4， ∴EC＝AE，∴BE＝AE. ∵CF＝AE， ∴BE＝EC＝CF＝BF， ∴四边形BECF是菱形； (2)当∠A＝45°时，菱形BECF是正方形． 证明如下：∵∠A＝45°，∠ACB＝90°， ∴∠CBA＝45°，∴∠EBF＝2∠CBA＝90°， ∴菱形BECF是正方形． 方法总结 正方形的判定方法：①先判定四边形是矩形，再 判定这个矩形有一组邻边相等；②先判定四边形是菱 形，再判定这个矩形有一个角为直角；③还可以先判 定四边形是平行四边形，再用①或②进行判定． 例7 如图，△ABC中，点O是AC上的一动点，过点O 作直线MN∥BC，设MN交∠BCA的平分线于点E，交 ∠BCA的外角∠ACG的平分线于点F，连接AE、AF. (1)求证：∠ECF＝90°； (2)当点O运动到何处时，四边形AECF是矩形？请 说明理由； (1)证明：∵CE平分∠BCO， CF平分∠GCO， ∴∠OCE＝∠BCE，∠OCF＝∠GCF， ∴∠ECF＝ ×180°＝90°.1 2 (2)解：当点O运动到AC的中点时，四边形AECF是 矩形．理由如下： ∵MN∥BC， ∴∠OEC＝∠BCE，∠OFC＝∠GCF. 又∵CE平分∠BCO，CF平分∠GCO， ∴∠OCE＝∠BCE，∠OCF＝∠GCF， ∴∠OCE＝∠OEC，∠OCF＝∠OFC， ∴EO＝CO，FO＝CO， ∴OE＝OF. 又∵当点O运动到AC的中点时，AO＝CO， ∴四边形AECF是平行四边形. ∵∠ECF＝90°， ∴四边形AECF是矩形. 解：当点O运动到AC的中点时， 且满足∠ACB为直角时，四边形AECF是正方形． ∵由(2)知当点O运动到AC的中点时，四边形AECF 是矩形， 已知MN∥BC， 当∠ACB＝90°， 则∠AOF＝∠COE＝∠COF＝∠AOE＝90°， 即AC⊥EF， ∴四边形AECF是正方形． (3)在(2)的条件下，△ABC应该满足什么条件时， 四边形AECF为正方形． 针对训练 7.如图，两个含有30°角的完全相同的三角板ABC和 DEF沿直线FC滑动，下列说法错误的是（　　） A．四边形ACDF是平行四边形 B．当点E为BC中点时，四边形ACDF是矩形 C．当点B与点E重合时，四边形ACDF是菱形 D．四边形ACDF不可能是正方形 B 8.如图，在菱形ABCD中，对角线AC=6，BD=10， 则菱形ABCD的面积为______．30 A B CO D 9.如图，四边形ABCD是边长为2的正方形，点G是 BC延长线上一点，连接AG，点E、F分别在AG上， 连接BE、DF，∠1＝∠2，∠3＝∠4. (1)证明：△ABE≌△DAF； (2)若∠AGB＝30°，求EF的长． (1)证明：∵四边形ABCD是正方形， ∴AB＝AD. 在△ABE和△DAF中， ∴△ABE≌△DAF. (2) 解：∵四边形ABCD是正方形， ∴∠1＋∠4＝90°. ∵∠3＝∠4， ∴∠1＋∠3＝90°， ∴∠AFD＝90°. 在正方形ABCD中， AD∥BC， ∴∠1＝∠AGB＝30°. 在Rt△ADF中，∠AFD＝90°，AD＝2， ∴AF＝ ，DF＝1. 由(1)得△ABE≌△DAF， ∴AE＝DF＝1， ∴EF＝AF－AE＝ －1. 3 3 例8 在一个平行四边形中，若一个角的平分线把一 条边分成长是2cm和3cm的两条线段，求该平行四 边形的周长是多少. 解：如图，∵在平行四边形ABCD中，AB=CD， AD=BC，AD∥BC， ∴∠AEB=∠CBE． 又∠ABE=∠CBE, ∴∠ABE=∠AEB, ∴AB=AE． （1）当AE=2时，则平行四边形的周长=2(2+5)=14． （2）当AE=3时，则平行四边形的周长=2(3+5)=16． 分类讨论思想 考点四 本章解题思想方法 平行四边形的性质与判定中要是出现角平分线，常与 等腰三角形的性质和判定结合起来考查，当边指向不 明时需要分类讨论，常见的的模型如下： 方法总结 例9 如图，折叠长方形一边AD，点D落在BC边的点 F处，BC=10cm，AB=8cm，求： （1）FC的长； （2）EF的长． 方程思想 解：（1）由题意得AF=AD=10cm， 在Rt△ABF中，∵AB=8， ∴BF=6cm， ∴FC=BC-BF=10-6=4cm． （2）由题意可得EF=DE，可设DE的长为x， 在Rt△EFC中，(8-x)2+42=x2， 解得x=5， 即EF的长为5cm． 例10 如图，平行四边形ABCD中，AC、BD为对角 线，其交点为O，若BC=6，BC边上的高为4，试求 阴影部分的面积． 转化思想 解：∵四边形ABCD为平行四边形， ∴OA=OC，OB=OD. ∵AB∥CD， ∴∠EAO=∠HCO. 又∵ ∠AOE＝∠COH， ∴△AEO≌△CHO（ASA）， 同理可得△OAQ≌△OCG，△OPD≌△OFB， ∴S阴影=S△BCD， 则S△BCD= S平行四边形ABCD= ×6×4=12．1 2 1 2 E H Q G F P 谢 谢