八年级下数学课件：18-2-1 矩形 （共21张PPT）_人教新课标 21页

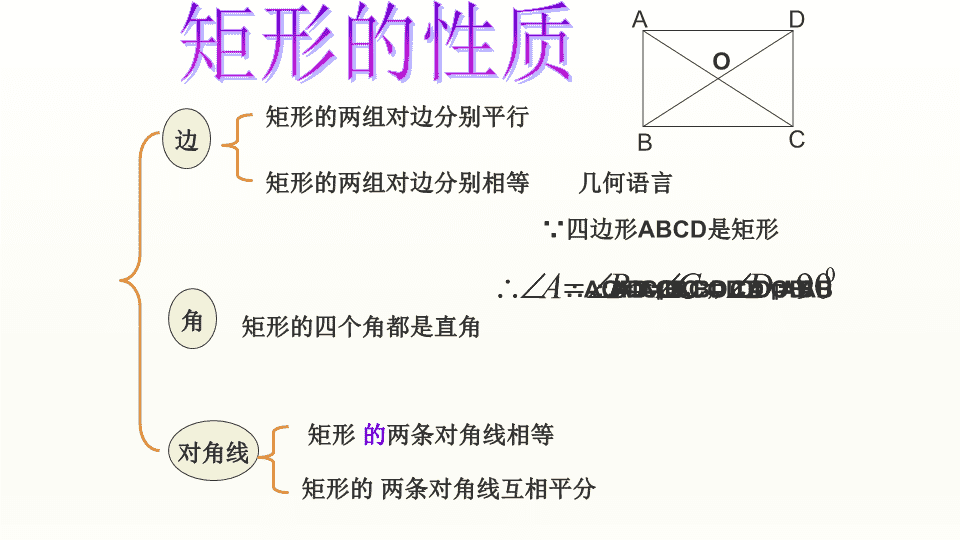
矩形 复习回顾 四边形 平行 四边形 两组对边 分别平行 一个角 是直角 ∟ 矩形 四边形集合 平行四边形集合 矩形集合 定义：有一个角是直角的平行四边形叫做矩形. 矩形的 两条对角线互相平分 矩形的两组对边分别相等 矩形的两组对边分别平行 矩形的四个角都是直角 矩形 的两条对角线相等 边 对角线 角 几何语言 ∵四边形ABCD是矩形 ∴AD = BC ，CD = AB∴AD ∥BC ，CD ∥AB∴AC= BD A B C D O ∴AO= CO ，OD = OB 090 DCBA • 四边形ABCD是矩形 1 若已知AB=8㎝，AD=6㎝， 则AC＝ ㎝ OB= ㎝ 2 若已知∠CAB=40°，则∠OCB= ∠OBA= ∠AOB= ∠AOD= 3 若已知AC＝10㎝，BC=6㎝，则矩形的周长＝ ㎝ 矩形的面积＝ ㎝2 4 若已知 ∠DOC=120°，AD＝6㎝，则AC= ㎝ O D C BA 5 50° 10 100°40° 12 48 28 80° 试一试 矩形的定义： 有一个角是直角的平行四边形是矩形. 你还有其它的判定方法吗？ ABCD ∠A=900 四边形ABCD是矩形 情境一：工人师傅为了检 验两组对边相等的四边形窗 框是否成矩形，一种方法是 量一量这个四边形的两条对 角线长度，如果对角线长相 等，则窗框一定是矩形吗？ 猜想：对角线相等的平行四边形是矩形 . 命题：对角线相等的平行四边形是矩形. 已知：平行四边形ABCD，AC=BD. 求证：四边形ABCD是矩形. A B C D 证明: ∵ AB=CD， BC=BC， AC=BD ∴ △ABC≌ △DCB（SSS） ∵ AB//CD ∴ ∠ABC+∠DCB=180° ∴ ∠ABC=∠DCB=90° 又∵ 四边形ABCD是平行四边形 ∴四边形ABCD是矩形 ∴ ∠ABC=∠DCB 对角线相等的平行四边形是矩形 . 矩形的判定方法： 几何语言： ∵四边形ABCD是平行四边形 AC=BD ∴四边形ABCD是矩形 （对角线相等且互相平分的四边形是矩形.） A B C D O （或OA=OC=OB=OD） 情境二：李芳同学有 “边——直角、边——直角、 边——直角、边”这样四步， 画出了一个四边形，她说这 就是一个矩形，她的判断对 吗？为什么？ 猜想：有三个角是直角的四边形是矩形 . 你能证明上述结论吗？ 矩形的判定方法： 有三个角是直角的四边形是矩形 . A B C D ∵ ∠A=∠B=∠C=90° ∴四边形ABCD是矩形 几何语言： 你能归纳矩形的几种判定方法吗？ 有一个角是直角的平行四边形是矩形. 对角线相等的平行四边形是矩形 . （对角线相等且互相平分的四边形是矩形.） 有三个角是直角的四边形是矩形 . 方法1： 方法2： 方法3： 下列各句判定矩形的说法是否正确？ （1）对角线相等的四边形是矩形； （2）对角线互相平分且相等的四边形是矩形； （3）有一个角是直角的四边形是矩形； （5）有三个角是直角的四边形是矩形； （6）四个角都相等的四边形是矩形； （7）对角线相等，且有一个角是直角的四边形是矩形； （10）一组邻边垂直，一组对边平行且相等的四边形是 矩形； （9）对角线相等且互相垂直的四边形是矩形； （8）一组对角互补的平行四边形是矩形； （4）有三个角都相等的四边形是矩形； 例：如图所示，在平行四边形ABCD中， 对角线AC,BD交于点O， 且OA=OD,∠OAD=50°, 求∠OAB的度数 D A B C O 有一个角是直角的平行四边形是矩形. 对角线相等的平行四边形是矩形 . （对角线相等且互相平分的四边形是矩形.） 有三个角是直角的四边形是矩形 . 方法1： 方法2： 方法3： 自我诊断 1、能够判断一个四边形是矩形的条件是（ ） A 对角线相等 B 对角线垂直 C对角线互相平分且相等 D对角线垂直且相等 2、矩形的一组邻边长分别是3cm和4cm，则它的对角线 长是 cm 3、如图，直线EF∥MN，PQ交EF、MN于A、C两点， AB、CB、CD、AD分别是∠ EAC、 ∠ MCA、 ∠ ACN、 ∠ CAF的角平分线，则四边形ABCD是（ ） A 菱形 B 平行四边形 C 矩形 D 不能确定 E F M N P Q A C DB C 5 C 例1：如图，M为平行四边形ABCD 边AD的中点，且MB=MC， 求证：四边形ABCD是矩形. A B C DM 例2：平行四边形ABCD，E是CD的中点， △ABE是等边三角形， 求证:四边形ABCD是矩形. D A B CE 例3：已知，如图．矩形ABCD的对角线 AC、BD相交于点O，且E、F、G、H分 别是AO、BO、CO、DO的中点， 求证：四边形EFGH是矩形． 例4： 如果平行四边形四个内角的平分线能够围成一个四边形，那 么这个四边形是矩形． 已知：如图， ABCD的四个内角的平 分线分别相交于E、F、G、H， 求证：四边形 EFGH为矩形． ∴∠BGC=90° 同理可证∠AFB=∠AED=90° ∴四边形EFGH是矩形．(有三个角是直角的四边形是矩形) 证明：∵AB∥CD 　　∴∠ABC＋∠BCD=180° 　　∵BG平分∠ABC，CG平分∠BCD　　 例5：已知MN∥PQ，同旁内角的平分线 AB、BC和AD、CD分别相交于点B、D． （1）猜想AC和BD间的关系是______； （2）试用理由说明你的猜想． 例6：在平行四边形ABCD中，对角线 AC BD相交于O，EF过O，且AF⊥BC， 求证:四边形AFCE是矩形 A B C D O F E