八年级下册数学教案 2-3 第1课时 中心对称及其性质 湘教版 2页

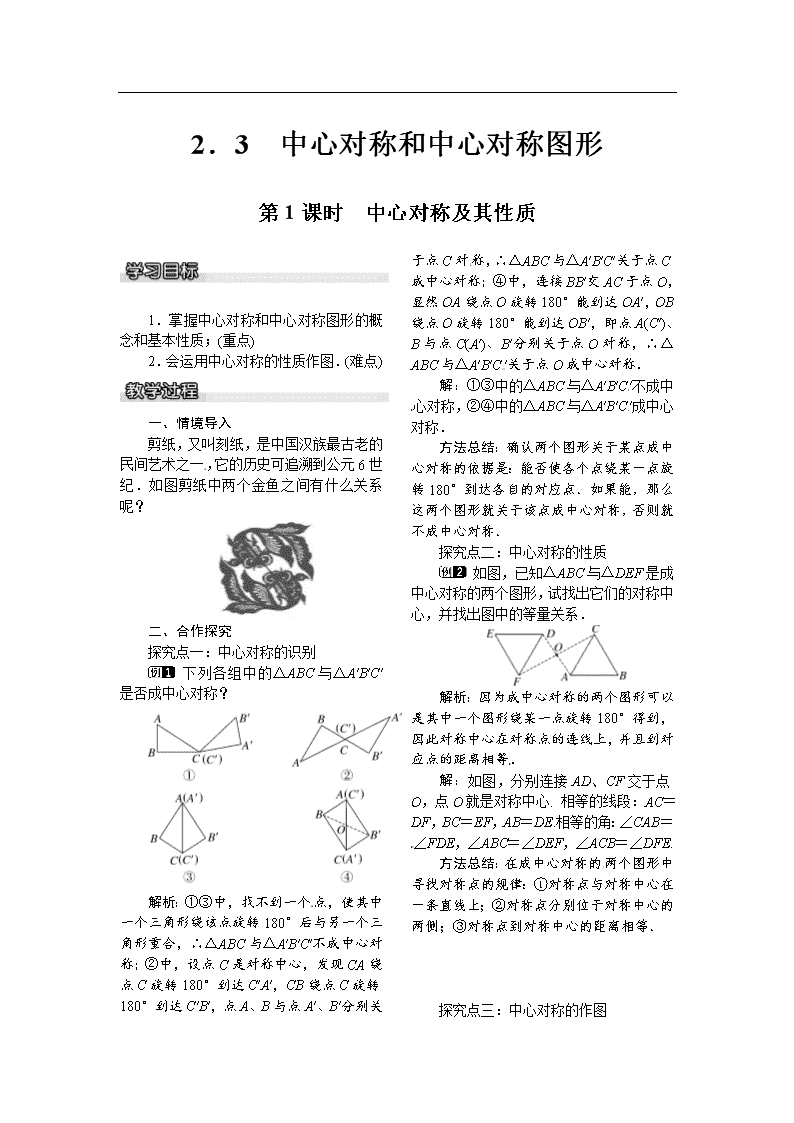
‎2．3　中心对称和中心对称图形 第1课时　中心对称及其性质 ‎1．掌握中心对称和中心对称图形的概念和基本性质；(重点)‎ ‎2．会运用中心对称的性质作图．(难点)‎ 一、情境导入 剪纸，又叫刻纸，是中国汉族最古老的民间艺术之一，它的历史可追溯到公元6世纪．如图剪纸中两个金鱼之间有什么关系呢？‎ 二、合作探究 探究点一：中心对称的识别 ‎ 下列各组中的△ABC与△A′B′C′是否成中心对称？‎ 解析：①③中，找不到一个点，使其中一个三角形绕该点旋转180°后与另一个三角形重合，∴△ABC与△A′B′C′不成中心对称；②中，设点C是对称中心，发现CA绕点C旋转180°到达C′A′，CB绕点C旋转180°到达C′B′，点A、B与点A′、B′分别关于点C对称，∴△ABC与△A′B′C′关于点C成中心对称；④中，连接BB′交AC于点O，显然OA绕点O旋转180°能到达OA′，OB绕点O旋转180°能到达OB′，即点A(C′)、B与点C(A′)、B′分别关于点O对称，∴△ABC与△A′B′C′关于点O成中心对称．‎ 解：①③中的△ABC与△A′B′C′不成中心对称，②④中的△ABC与△A′B′C′成中心对称．‎ 方法总结：确认两个图形关于某点成中心对称的依据是：能否使各个点绕某一点旋转180°到达各自的对应点．如果能，那么这两个图形就关于该点成中心对称，否则就不成中心对称．‎ 探究点二：中心对称的性质 ‎ 如图，已知△ABC与△DEF是成中心对称的两个图形，试找出它们的对称中心，并找出图中的等量关系．‎ 解析：因为成中心对称的两个图形可以是其中一个图形绕某一点旋转180°得到，因此对称中心在对称点的连线上，并且到对应点的距离相等．‎ 解：如图，分别连接AD、CF交于点O，点O就是对称中心. 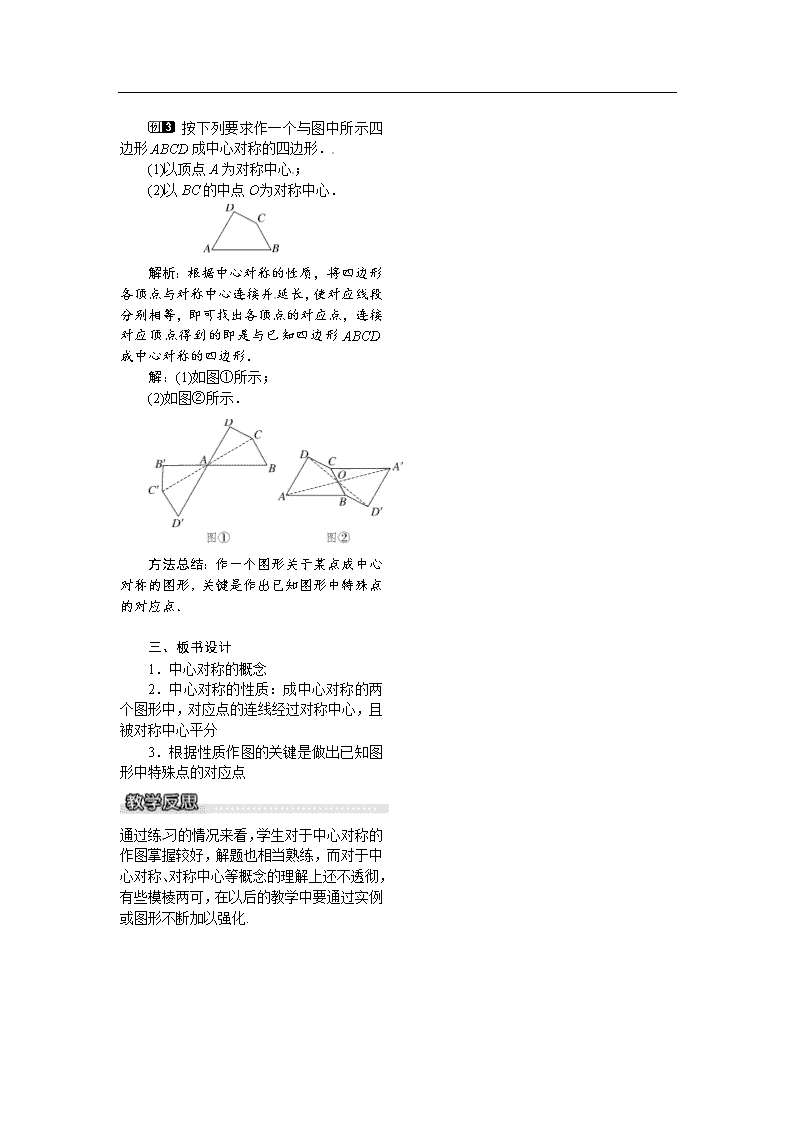相等的线段：AC＝DF，BC＝EF，AB＝DE.相等的角：∠CAB＝∠FDE，∠ABC＝∠DEF，∠ACB＝∠DFE.‎ 方法总结：在成中心对称的两个图形中寻找对称点的规律：①对称点与对称中心在一条直线上；②对称点分别位于对称中心的两侧；③对称点到对称中心的距离相等．‎ ‎[来源:Zxxk.Com]‎ 探究点三：中心对称的作图 ‎[来源:Z,xx,k.Com]‎ ‎ 按下列要求作一个与图中所示四边形ABCD成中心对称的四边形．‎ ‎(1)以顶点A为对称中心；‎ ‎(2)以BC的中点O为对称中心．‎ 解析：根据中心对称的性质，将四边形各顶点与对称中心连接并延长，使对应线段分别相等，即可找出各顶点的对应点，连接对应顶点得到的即是与已知四边形ABCD成中心对称的四边形．‎ 解：(1)如图①所示；‎ ‎(2)如图②所示．[来源:学科网ZXXK]‎ 方法总结：作一个图形关于某点成中心对称的图形，关键是作出已知图形中特殊点的对应点．‎ ‎[来源:学科网ZXXK]‎ 三、板书设计[来源:学_科_网]‎ ‎1．中心对称的概念 ‎2．中心对称的性质：成中心对称的两个图形中，对应点的连线经过对称中心，且被对称中心平分 ‎3．根据性质作图的关键是做出已知图形中特殊点的对应点 通过练习的情况来看，学生对于中心对称的作图掌握较好，解题也相当熟练，而对于中心对称、对称中心等概念的理解上还不透彻，有些模棱两可，在以后的教学中要通过实例或图形不断加以强化.‎