八年级上数学课件- 11-3-2 多边形及其内角和 课件（共23张PPT）_人教新课标 23页

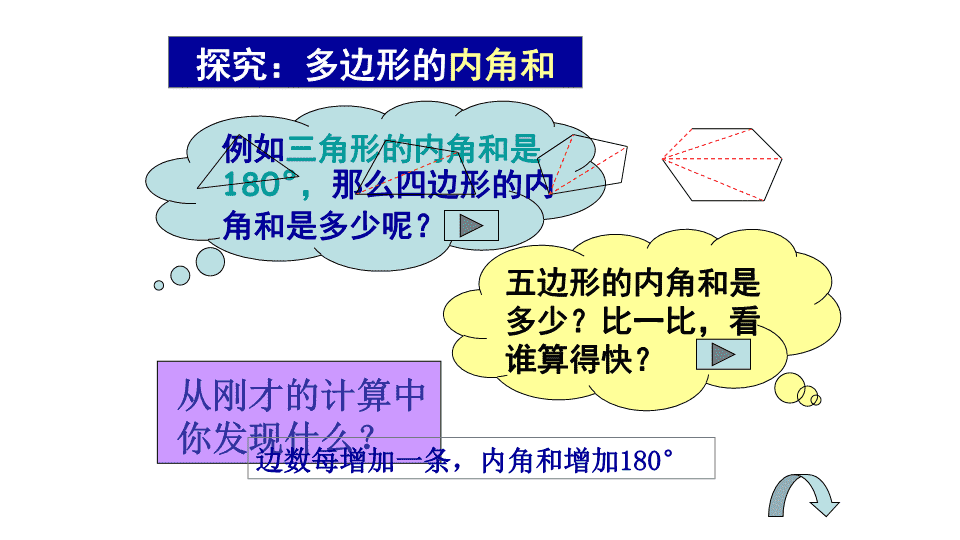
人教版数学实验教材七年级下册 复习提问： • 1、什么三角形、多边形？ • 2、三角形的内角和、外角和各是多少？ 探究：多边形的内角和 从刚才的计算中 你发现什么？边数每增加一条，内角和增加180° 例如三角形的内角和是 180°，那么四边形的内 角和是多少呢？ 五边形的内角和是 多少？比一比，看 谁算得快？ 由少到多，归纳多边形的内角和 三角形内角和等于180°A B C A C D B 从四边形的一个顶点出发 可以引 条对角线, 它们将四边形分为 个 三角形,四边形的内角和等 于180 °× . 2 2 = 360 ° 1 由少到多，归纳多边形的内角和 三角形内角和等于1800 A B C A C D E B 从五边形的一个顶点出发 可以引 条对角线, 它们将五边形分为 个 三角形,五边形的内角和等 于180 °× . 3　 3 = 540 ° 　 2　 多边形 的边数 图 形 分割出的三 角形的个数 多边形的 内 角 和 3 4 5 ----- ------ ------ ------ n n-2 1 1×180º 2 2×180º 3 3×180º (n-2)×180º 研究问题的方法是： 　　从简单入手---观察、归纳（寻找 规律）---猜想结论---验证 多边形 的边数 图 形 分割出的三 角形的个数 多边形的 内 角 和 3 4 5 ----- ------ ------ ------ n n-1 1 1×180º 3 3×180º－180º 4 4×180º－ 180º (n-1)×180º－ 180º 多边形 的边数 图 形 分割出的三 角形的个数 多边形的 内 角 和 3 4 5 ----- ------ ------ ------ n n 1 1×180º 4 　 4×180º－360º 5 　5×180º－360º n×180º－ 360º 　　你能参考以上三种方法推导多 边形内角和公式的过程，再用第四 种方法推导多边形内角和吗？ 三角形　　　四边形　　五边形　　　n边形 n边形的内角和公式是： (n-2)×180° 多边形的内角和与边数有关， 与形状、大小无关。 【课堂练习】 • (1)五边形的内角和等于 ； • (2)十二边形的内角和等于 。 • (3)若一个多边形的内角和为1080°，那 么它是 边形； • (4)多边形的边数每增加一边，它的内角 和就增加 ° 。 • (5)正八边形的内角和等于 °，每一 个内角等于 　 °。 540° 1800 ° 10 1080 180 135 例1、如果一个四边形的一组对角互补，那么 另一组对角有什么关系？ • 解：四边形ABCD中， ∠A+∠C=180°， • 又因为 ∠A+∠B+∠C+∠D • =（4-2）×180° • =360°， • 所以∠B+∠D=360°-（∠A+∠C） • =360°-180° • =180° • 这就是说，如果一个四边形的一组对角互补， 那么另一组对角也互补。 例题 D C A B 例2、如图，在六边形的每个顶点处各取一个外角， 这些外角的和叫做六边形的外角和。 六边形的外角和等于多少？ • 思考： • 1、任何一个外角同与它相邻的内 角有什么关系？它们的和是多少 度？ • 2、六边形的6个外角加上与它们 相邻的6个内角，所得的总和是多 少？ • 3、上述总和与六边形的内角和、 外角和有什么关系？你能从中找 到求六边形外角和的方法吗？ 例题 提出问题 1、多边形的每一个外角与和它相邻的内角之 间是什么关系？ 2、一个n边形，它的内角和由边数n决定， 那么它的外角和也由 边数n决定吗？ 课件动画演示：汽车转圈——多边形外角和实例演示。 多边形的 边数 3 4 5 6 … n 多边形的 内角与外 角的总和 3×180° =540° … 多边形的 内角和 180° … 多边形的 外角和 540° －180° =360° … 4×180° =720° 5×180° =900° 6×180° =1080° 360° 540° 720° 720° －360° =360° 900° －540° =360° 1080° －720° =360° • 思考： • 1、多边形的外角和与多边形的边数有 关吗？内角和呢？ • 2、改变多边形的形状，它的外角和会 改变吗？内角和呢？ 归纳：多边形外角和=360° • 若一个多边形的每个内角都是108°，则这 个多边形的边数是 。 小比赛：看谁算得快！ 解法1： 　　设它是n边形，则有： n180°=（n-2）×180°， 解得n=5 解法2： 360°÷（180°-108°）=5 【基础练习】 1、如果正多边形的一个外角为72°，那么它 的边数是　　　　。 2、正八边形的内角和为 ，外角和为 ， 每个内角度数为 ，每个外角度数 为 。 3、已知多边形的内角和与外角和相等，则这 个多边形的边数为 。 　　【尝试练习】 • 课本P85、P86#“练习”1、2、3 【小组研究，共同提高】 【问题1】 　　某同学在求凸多边形内角和 时，因为漏算了一个角，算得结 果为2400°，你能帮他求出漏算 的那个角吗？ 【问题2】满足下列条件的正多边形是否 存在，若存在，请说出是几边形： （3）每个内角均为100°. （1）每个内角均为60°； 讨论 （2）每个内角均为140°； 正三角形 正九边形 不存在 （4）一个多边形的内角和不可能是（ ）。 　　　（A）1800°　（B）360° 　　　（C）1080° （D）910° D 【小结】说一说你的收获 　1、多边形内角和公式为 　　　（n-2）×180°， 　　所以：多边形的内角和 一定是180°的倍数。 2、n边形n个外角的和为固定 值360°，与边数无关。