浙教版数学八年级上册《一次函数》练习 5页

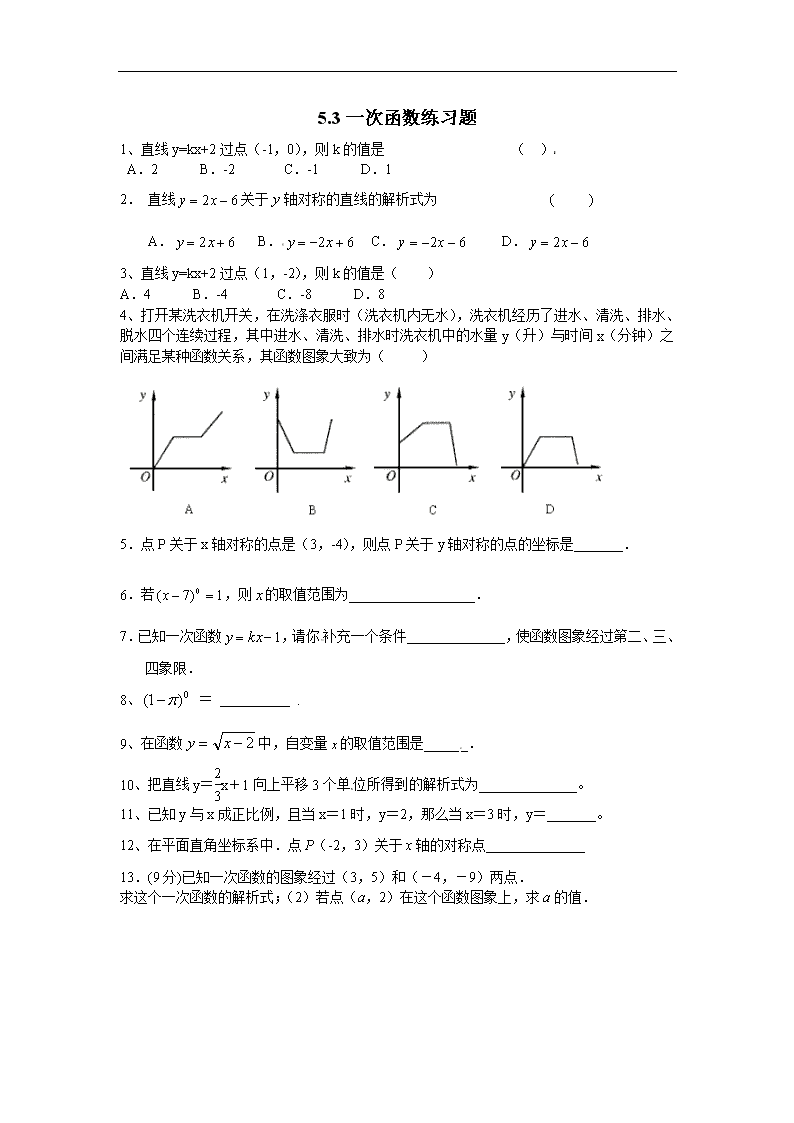
5.3 一次函数练习题 1、直线 y=kx+2 过点（-1，0），则 k 的值是 （ ） A．2 B．-2 C．-1 D．1 2． 直线 62  xy 关于 y 轴对称的直线的解析式为 ( ) A． 62  xy B． 62  xy C． 62  xy D． 62  xy [ 3、直线 y=kx+2 过点（1，-2），则 k 的值是（ ） A．4 B．-4 C．-8 D．8 4、打开某洗衣机开关，在洗涤衣服时（洗衣机内无水），洗衣机经历了进水、清洗、排水、 脱水四个连续过程，其中进水、清洗、排水时洗衣机中的水量 y（升）与时间 x（分钟）之 间满足某种函数关系，其函数图象大致为（ ） 5．点 P 关于 x 轴对称的点是（3，-4），则点 P 关于 y 轴对称的点的坐标是_______． 6．若 1)7( 0 x ，则 x 的取值范围为__________________． 7．已知一次函数 1 kxy ，请你 补充一个条件______________，使函数图象经过第二、三、 四象限． 8、 0(1 ) ＝ . 9、在函数 2 xy 中，自变量 x 的取值范围是______． 10、把直线 y＝2 3x＋1 向上平移 3 个单位所得到的解析式为______________。 11、已知 y 与 x 成正比例，且当 x＝1 时，y＝2，那么当 x＝3 时，y＝_______。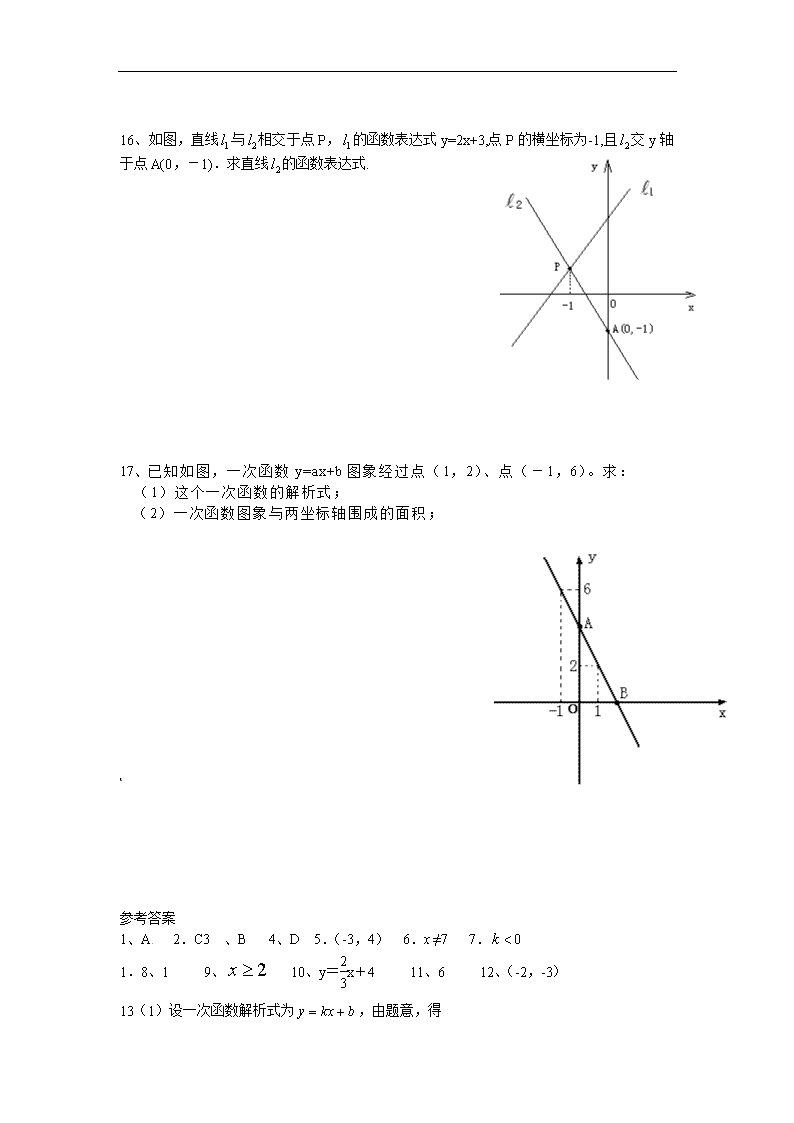 12、在平面直角坐标系中．点 P（-2，3）关于 x 轴的对称点 13．(9 分)已知一次函数的图象经过（3，5）和（－4，－9）两点． 求这个一次函数的解析式；（2）若点（a，2）在这个函数图象上，求 a 的值． 14．如图，直线 y=－2x+4 分别与 x 轴、y 轴相交于点 A 和点 B，如果线段 CD 两端点在坐 标轴上滑动(C 点在 y 轴上，D 点在 x 轴上)，且 CD=AB． 当△COD 和△AOB 全等时，求 C、D 两点的坐标； 15、已知直线 3y kx  经过点 M ，求此直线与 x 轴， y 轴的交点坐标． x y O A B 3y kx  y xO M 1 1 2 16、如图，直线 1l 与 2l 相交于点 P， 1l 的函数表达式 y=2x+3,点 P 的横坐标为-1,且 2l 交 y 轴 于点 A(0，－1)．求直线 2l 的函数表达式. 17、已知如图，一次函数 y=ax+b 图象经过点（1，2）、点（－1，6）。求： （1）这个一次函数的解析式； （2）一次函数图象与两坐标轴围成的面积； 参考答案 1、A 2．C3 、B 4、D 5．（-3，4） 6．x ≠7 7． 0k 1．8、1 9、 2x  10、y＝2 3x＋4 11、6 12、（-2，-3） 13（1）设一次函数解析式为 bkxy  ，由题意，得 3 5 4 9. k b k b       ， …………… 解之，得 2, 1. k b     ………………………… 因此一次函数的解析式为 12  xy ．………………………… （2）将（ a ，2）代入 12  xy ，得 212 a ． …………………… 解得 2 3a ． …………………………………………………… 14．（1）由题意，得 A（2，0），B（0，4）， 即 AO=2 OB=4． …………………………………………………2 分 ①当线段 CD 在第一象限时， 点C（0，4），D（2，0）或 C（0，2），D（4，0）．……………… ②当线段 CD 在第二象限时， 点 C（0，4），D（－2，0）或 C（0，2），D（－4，0）．…………… ③当线段 CD 在第三象限时， 点 C（0，－4），D（－2，0）或 C（0，－2），D（－4，0）．…… ④当线段 CD 在第四象限时， 点C（0，－4），D（2，0）或 C（0，－2），D（4，0） ……… 15、P120 习题 8 改造题 解：由图象可知，点 ( 21)M  ， 在直线 3y kx  上， 1 分 2 3 1k   解得 2k   ． 直线的解析式为 2 3y x   ． 令 0y  ，可得 3 2x   ． 令 0x  ，可得 3y   ． ∴直线与 x 轴的交点坐标为 3 02     ， ， y 轴的交点坐标为 (0 3)， 16、解：设点 P 坐标为（-1，y）,代入 y=2x+3,得 y=1，∴点 P（-1，1）. 设直线 2l 的函数表达式为 y=kx+b,把 P（-1，1）、A（0，-1）分别代入 y=kx+b，得 1=-k+b， -1=b，∴k=-2，b=-1. ∴直线 2l 的函数表达式为 y=-2x-1. 8 分 17、解：(1)依题意，当 x=1 时，y=2；当 x=-1 时，y=6，则      ba ba 6 2 ……………2 分 解之得      4 2 b a ..............4 分 ∴一次函数解析式为： 42  xy ..............8 分 （2）一次函数图象与 y 轴、x 轴分别相交于 A、B 两点，由 42  xy ，得 A 点坐标（0，4），B 点坐标（ 2，0）..............10 分 即 OA=4，OB=2 ∴S△AOB= OBOA 2 1 = 242 1  =4 即一次函数图象与两坐标轴围成的面积为 4 ……