八年级数学上册第七章平行线的证明4平行线的性质教案 北师大版 4页

1 4 平行线的性质 【知识与技能】 经历探索平行线的性质的过程，初步掌握平行线的性质，并能用性质进行简单的推理和 计算. 【过程与方法】 在学习过程中进一步培养学生的推理能力.发展学生的空间观念. 【情感态度】 培养学生的唯物主义观点，使学生逐步养成言之有据的习惯. 【教学重点】 平行线性质的探索及性质的理解. 【教学难点】 运用平行线的性质和判定结合去解决问题. 一、创设情境，导入新课 现在同学们已经掌握了利用同位角相等，或者内错角相等，或者同旁内角互补，判定两 条直线平行的三种方法.在这一节课里：大家把思维的指向反过来：如果两条直线平行，那 么同位角、内错角、同旁内角的数量关系又该如何表达？ 【教学说明】了解学生的认知基础，让全体学生对前一节的内容进行回顾，并为新课程 的学习做准备. 二、思考探究，获取新知 平行线的性质及其证明. 问题 1：我们已经探索过平行四边形的性质，两直线平行，同位角相等，那它如何证明 呢？ 【教学说明】给学生留有充分的探索和交流的空间，鼓励学生利用多种方法探索，这对 于发展学生的空间观念，理解平行线的性质是十分重要的.此题的证明可以让学生感受反证 法. 问题 2：利用上面的定理，你能证明其他两条性质吗？试一试！ 【教学说明】培养学生的逻辑思维能力以及严谨的治学态度，逐步锻炼学生的推理能力， 并进一步巩固对定理的理解及语言的规范，感受成功的喜悦，树立学习数学的信心. 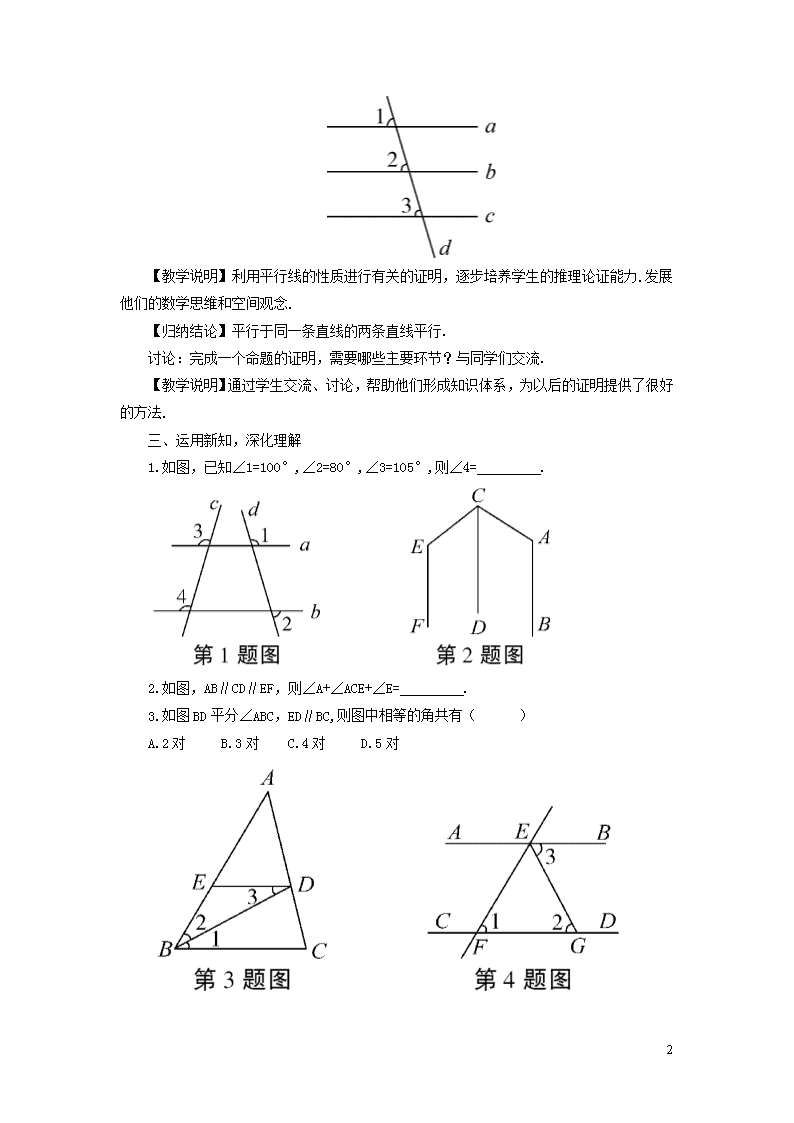问题 3： 例 已知：如图，b∥a,c∥a,∠1,∠2,∠3 是直线 a、b、c 被直线 d 截出的同位角.求证： b∥c. 2 【教学说明】利用平行线的性质进行有关的证明，逐步培养学生的推理论证能力.发展 他们的数学思维和空间观念. 【归纳结论】平行于同一条直线的两条直线平行. 讨论：完成一个命题的证明，需要哪些主要环节？与同学们交流. 【教学说明】通过学生交流、讨论，帮助他们形成知识体系，为以后的证明提供了很好 的方法. 三、运用新知，深化理解 1.如图，已知∠1=100°,∠2=80°,∠3=105°,则∠4= . 2.如图，AB∥CD∥EF，则∠A+∠ACE+∠E= . 3.如图 BD 平分∠ABC，ED∥BC,则图中相等的角共有（ ） A.2 对 B.3 对 C.4 对 D.5 对 3 4.如图，已知 AB∥CD,直线 EF 分别交 AB、CD 于 E、F，EG 平分∠BEF，∠1=40°.求∠2 的度数. 5.如图，已知 A、B、C 同在一条直线上,D、E、F 同在一条直线上，且∠A=∠F,∠C=∠D, 判断 AE 与 BF 的位置关系，并说明理由. 【教学说明】通过对练习的处理，培养学生的口语表达能力和逻辑推理能力.使学生逐 步学会运用推理的方法去证明问题，在具体的问题情境中能自觉地运用转化的思想去解决问 题.对学习有困难的学生教师及时给予指导和点拨. 【答案】1.105°；2.360°；3.D. 4.解：∵AB∥CD,∴∠BEF=180°-∠1=180°-40°=140°. 又∵EG 平分∠BEF,∴∠3= 1 2 ∠BEF= 1 2 ×140°=70°. ∵AB∥CD,∴∠2=∠3=70°. 5.AE∥BF. 证明：∵∠C=∠D,∴DF∥AC.∴∠A=∠1, ∵∠A=∠F,∴∠1=∠F.∴AE∥BF. 四、师生互动，课堂小结 1.师生共同回顾平行四边形的三条判定性质以及由例题得出的一个结论. 2.谈谈你对本节课的收获与不足. 【教学说明】通过引导学生回顾平行线的判定与性质.加强它们之间的区别和联系，进 一步体会综合运用过程中的方法思路. 4 1.布置作业：习题 7.5 中的第 1、2、3、4 题. 2.完成练习册中本课时相应练习. 本节课主要是平行线性质定理的推理，重在培养学生的逻辑思维能力和规范的推理过程 的表述.再到平行线的性质与判定的综合运用，加深对所学知识的认识，提高运用知识解决 实际问题的能力.在证明的过程中，图形有着至关重要的辅助作用.